Определительные испытания на надежность

Определительные испытания проводятся с целью оценки фак­тической надежности ЭА. При этом оцениваются либо непосред­ственно показатели надежности, либо параметры законов распре­деления случайных величин, обусловливающих надежность ЭА, таких как время до отказа или между отказами, время до наступ­ления предельного состояния, время восстановления и др. Здесь речь идет об оценке надежности, а не об определении истинных значений показателей надежности по следующим причинам: ис­пытания на надежность часто носят выборочный характер и ре­зультаты испытаний выборки распространяются на всю партию изготовленных ЭА, что вносит элемент случайности в результаты оценки надежности партии; число испытываемых изделий (раз­мер выборки) является ограниченным, а результаты испытаний имеют случайный характер.

Оценкой показателя надежности называют формальную зави­симость, связывающую зафиксированные в процессе испытаний статистические, экспериментальные данные со значением оцени­ваемого показателя. Различают точечные и интервальные оценки показателей надежности. Первые представляют собой средние чи­словые характеристики наблюдаемых в процессе испытаний слу­чайных величин, определяющих надежность испытываемых из­делий.

Наиболее распространенными точечными оценками являются выборочное среднее и выборочная дисперсия. Предположим, что для оценки средней наработки до отказа проведены испытания п изделий, т. е. проведены испытания выборки размером п. При этом испытания проводились до отказа всех ЭА, вследствие чего получены п реализаций, t₁, t₂,..., t_n случайной величины Т — вре­мени до отказа. Для получения формулы, связывающей оценку средней наработки до отказа Т* с полученными значениями слу­чайной величины t_i(i = 1,..., п), воспользуемся так называемым методом максимального правдоподобия. В его основе лежит утверждение, что если в опыте наблюдались какие-то значения случайных величин, то именно эти значения являются наиболее вероятными. Можно считать, что исход опыта определяется со­вокупностью (вектором) одинаково распределенных независи­мых п случайных величин — промежутков времени от включе­ния до отказа каждого изделия. Введем понятие о функции правдо­подобия 𝚯 как о совместной n-мерной плотности распределения вероятностей события, заключающегося в том, что в процессе ис­пытаний случайная величина Т примет значение для первого изде­лия t₁, для второго — t₂, для n-го — t_n. Полагая, что время до от­каза распределено по экспоненциальному закону, получим

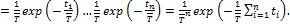(13.1)

Функция правдоподобия зависит от неизвестного значения средней наработки до отказа, оценку которой мы ищем. Исходя из принципа максимального правдоподобия, значение 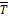должно быть таким, чтобы функция 𝚯 принимала максимальное значение. Та­ким образом, приходим к необходимости максимизировать функ­цию (или ее логарифм, что удобнее) по 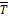. Прологарифмируем функцию 𝚯 и найдем производную по :

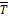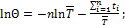(13.2)

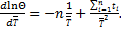(13.3)

Определим значение при котором функция правдопо­добия будет иметь максимум:

(13.4)

Отсюда получаем формулу для оценки средней наработки до отказа:

(13.5)

Эту оценку называют также выборочным средним.

Другой точечной оценкой в данном случае является выбороч­ная дисперсия

(13.6)

Такие сравнительно простые и очевидные оценки получились в результате того, что был рассмотрен самый простой план испы­таний — до отказа всех ЭА в выборке.

План испытаний на надежность представляет собой ряд указа­ний по проведению испытаний. К числу этих указаний относятся:

а) число ЭА, подлежащих испытаниям, или размер выборки п;

б) подлежат или нет замене отказавшие ЭА (первый вариант обозначают буквой В — восстановление, второй — Б — без восста­новления);

в) продолжительность испытаний. Здесь возможны такие ва­рианты:

■ испытания должны продолжаться в течение заданного време­ни Т (обозначение в плане — Т);

■ испытания должны быть прекращены в момент времени t_r, где r — заданное число отказов за время испытаний (обозначе­ние — r);

■ испытания должны быть прекращены в момент времени t_r если t_r < Т, или в момент Т, если t_r ≥ Т (обозначения в плане — r, Т). Можно назвать шесть различных планов испытаний на надеж­ность: [n, В, Т ], [n, В, r], [n, В, (r, Т)],[n, Б, T ], [ п, Б, r], [n, Б, (r, T)].

Например, план испытаний на надежность [ п, Б, (r, Т)]означает следующее: испытаниям должны подвергнуться п ЭА; отказавшие ЭА должны заменяться новыми; испытания должны быть прекра­щены в момент t_r наступления r-го отказа (число r задается), если t_r < T, либо продолжаться заданное время Т, если t_r ≥ Т. Для этих шести планов с помощью метода максимального правдоподобия получены формулы оценки интенсивности отказов в предположе­нии, что время до отказа распределено по экспоненциальному за­кону [6] (табл. 13.1).

Планирование определительных испытаний для получения точечных оценок возможно лишь ориентировочное — по предпо­лагаемой надежности, которая может быть определена либо пу­тем расчета на этапе проектирования ЭА, либо путем сравнения с аналогами, для которых надежность известна. Для экспоненци­ального распределения времени до отказа средняя продолжитель­ность испытаний для получения r отказов составит

(13.7)

где λ — расчетное значение интенсивности отказов ЭА (либо зна­чение, определенное сравнением с аналогами).

Планирование по среднему значению продолжительности ис­пытаний может привести к большим ошибкам. Более уверенное планирование можно проводить по вероятности получения необ­ходимого числа отказов за время испытаний:

(13.8)

Принимая эту вероятность достаточно высокой (≥ 0,9) и зада­вая две величины из трех (n, r, t_и), по данному выражению можно определить третью.

Точечные оценки показателей надежности не позволяют непо­средственно судить о точности и достоверности оцениваемых по­казателей. Поэтому в теории надежности получили распростране­ние так называемые интервальные оценки, когда по результатам испытаний рассчитываются нижняя и верхняя доверительные гра­ницы исследуемого показателя. Доверительный интервал с задан­ной вероятностью (доверительной вероятностью) «накрывает» ис­тинное значение искомого показателя. Таким образом, можно на­писать соотношение

(13.9)

где Н _H, Н _B — нижняя и верхняя доверительные границы опреде­ляемого показателя надежности; Н — истинное (неизвестное) зна­чение определяемого показателя надежности; Р* — доверительная вероятность, которая выбирается из ряда чисел 0,8; 0,9; 0,95; 0,99.

Доверительный интервал характеризует значение ошибки при оценке показателя надежности, доверительная вероятность — дос­товерность оценки. Чем меньше информации о надежности по ре­зультатам испытаний (небольшое число испытываемых изделий, малое число зафиксированных отказов) и чем выше выбранное зна­чение доверительной вероятности, тем больший доверительный интервал получается. При оценке показателя надежности с помо­щью доверительного интервала всегда существует риск ошибиться, т. е. истинное значение неизвестного показателя не будет «накры­то» найденным доверительным интервалом. Вероятность такой ошибки будем называть уровнем значимости α. Уровень значимо­сти и доверительная вероятность — вероятности противополож­ных событий, поэтому

(13.10)

Рассмотрим два примера определения доверительных интер­валов для показателей надежности по результатам испытаний. Нужно заметить, что в основе метода нахождения доверительных интервалов лежит то обстоятельство, что сама оценка показателя надежности является случайной величиной и нахождение дове­рительного интервала сводится к отысканию функции распреде­ления этой случайной величины и затем определению интервала, в который эта случайная величина попадает с вероятностью, рав­ной доверительной вероятности Р*.

Определение доверительного интервала для средней наработ­ки на отказ. Пусть испытывается один восстанавливаемый ЭА, для которого известно, что промежутки времени между отказами t_i рас­пределены по экспоненциальному закону. Предположим, что в результате испытаний зафиксировано r отказов и момент наступ­ления последнего отказа равен t_r, который и определил суммар­ную наработку ЭА за время испытаний (предполагается, что вре­мя на восстановление мало и им можно пренебречь):

(13.11)

где t_i — случайный промежуток времени между (i - 1)-м и i-м от­казами.

Определим доверительный интервал для средней наработки на отказ по известным r, t_r и заданному значению доверительной вероятности Р*. С этой целью необходимо определить нижнюю и верхнюю доверительные границы _H и _Bсредней наработки на отказ, для которых справедливо равенство

(13.12)

где — истинное (неизвестное) значение средней наработки на отказ.

Чтобы решить эту задачу, можно воспользоваться известным в математической статистике фактом, что при экспоненциаль­ном распределении случайных промежутков времени между со­седними отказами t_i величина 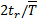имеет χ²-распределение с 2r степенями свободы, т. е. плотность распределения вероятно­стей этой величины:

(13.13)

где —гамма-функция.

 

 

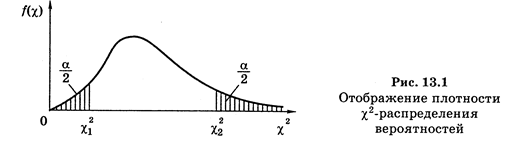
Кривая плотности χ²-распределения вероятностей представле­на на рис. 13.1.

По плотности распределения можно определить вероятность попадания случайной величины χ² на заданный интервал. Если он будет соответствовать доверительному интервалу, то эта веро­ятность будет доверительной вероятностью. Таким образом, для нижней границы интервала и верхней границы интервала 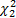будем иметь

(13.14)

где — площадь под кривой плотности распределения веро­ятностей от начала координат до значения — площадь под кривой плотности распределения вероятностей от начала ко­ординат до значения

Воспользуемся понятием о квантиле случайной величины. Как известно, квантилем случайной величины X называют такое зна­чение случайной величины х_p, для которого с вероятностью 1 - р можно утверждать, что полученное значение этой случайной ве­личины попадает в интервал (-∞, х_p). Можно доказать, что длина доверительного интервала при заданном значении Р* будет наи­меньшей, если величина

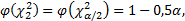(13.15)

а величина

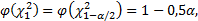(13.16)

т. е. когда заштрихованные на рис. 13.1 области равны по площа­ди. Здесь — квантили χ²-распределения с вероятно­стями соответственно Таким образом, получаем

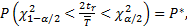(13.17)

откуда следует, что при заданном значении Р* = 1 - α справедливо неравенство

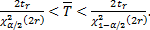(13.18)

Тогда

(13.19)

(13.20)

Значения квантилей находят по табли­цам χ²-распределения с 2r степенями свободы. Приведенные фор­мулы могут быть использованы при экспоненциальном распреде­лении времени между отказами (или до отказа) и для случая, ко­гда испытывается несколько однотипных восстанавливаемых или невосстанавливаемых ЭА и испытания заканчиваются в момент t_r наступления r-го отказа (отказы учитываются по всем ЭА). При этом t_r подсчитывается как суммарная наработка всех ЭА.

Приведем без вывода некоторые дополнительные результаты для этого случая. Если испытания продолжаются после r-го отка­за (но не до наступления (r+ 1)-го), то границы доверительного интервала находятся по формулам

(13.21)

(13.22)

Если в процессе испытаний отказы не наблюдались (r = 0), то определяется только нижняя граница наработки на отказ (одно­сторонний доверительный интервал) по формуле

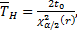(13.23)

где t₀ — суммарная продолжительность испытаний.

Определение доверительного интервала для средней наработ­ки до отказа для нормального распределения времени до отказа.

Пусть испытаниям подверглись п ЭА до отказа всех ЭА (r = n). В ка­честве исходной статистики, полученной по результатам этих ис­пытаний, зафиксированы п значений t_i случайной величины Т — времени от включения до отказа каждого ЭА. По этой статистике могут быть определены оценки средней наработки до отказа и сред­него квадратического отклонения величины Т по формулам

(13.24)

(13.25)

Оценка (13.24) средней наработки до отказа представляет собой случайную величину, являющуюся функцией от исходной случайной величины . Поскольку исходная случайная величи­на — время до отказа — распределена по нормальному закону, то и сама оценка распределена по такому же закону с параметрами:

(13.26)

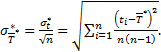(13.27)

Кривая плотности распределе­ния вероятностей оценки пред­ставлена на рис. 13.2. Это так на­зываемая нормированная кривая нормального распределения, которая может быть построена по таблицам функции

(13.28)

где

На этом рисунке на оси абсцисс деления отмечены цифрами, соответствующими числу средних квадратических отклонений 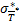, которые укладываются в промежуток от нулевого до данного де­ления, т. е. единицей измерения центрированной и нормирован­ной случайной величины X является среднее квадратическое от­клонение оценки

Введем квантиль К_а/2, с помощью которого определяется проме­жуток, равный (-К_а/2, К_а/2) (измеренный в количестве 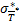.) и в пределы которого наша центрированная и нормированная случайная величина — оценка средней наработки до отказа X — попадает с вероятностью 1 - α, где α — уровень значимости, достаточно ма­лая величина. Вероятность попадания оценки левее -К_а/2, рав­ная α/2, и правее К_а/2, а также равная α/2, в сумме дают вероят­ность того, что наша оценка будет располагаться вне интервала (— К_а/2, К_а/2). На рис. 13.2 этим вероятностям соответствуют заштри­хованные площади. Для того чтобы перейти от центрированной и нормированной случайной величины X к исходной случайной вели­чине — оценке средней наработки до отказа, следует вспомнить, что нулевому значению величины X соответствует величина , а зна­чениям величины X, равным ±К_а/2, — величины ±K_α/2

Таким образом определяется доверительный интервал для оценки средней наработки до отказа, нижняя и верхняя границы которого находятся по формулам:

(13.29)

(13.30)

Этот доверительный интервал «накрывает» истинное значение средней наработки до отказа с доверительной вероятностью

(13.31)

Иначе можно записать

(13.32)

Из таблиц нормального распределения можно установить, что истинное значение приблизительно в 68,3% случаев будет ле­жать в пределах ±1 среднего квадратического отклонения 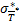, из­меренной оценки приблизительно в 95,4% —в пределах ±2 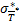и т. д.

Вероятности, выраженные в процентах для интервала ±K_a/2 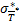(т. е. 68,3; 95,4 и т. д.), представляют собой доверитель­ные вероятности для соответствующих интервалов. Удобнее зна­чения доверительных интервалов выбирать из следующего ряда: 0,80; 0,90; 0,95; 0,99. Тогда соответствующие значения кванти­лей должны быть взяты из табл. 13.2.

Планирование определительных испытаний в рассмотренном случае производится на основании использования показателя точ­ности оценки средней наработки до отказа

(13.33)

ожидаемого среднего квадратического отклонения и довери­тельной вероятности Р*. По этим величинам определяется необхо­димое число п изделий, подлежащих испытаниям.

 

13.3

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: