Основные сведения о конвективном теплообмене

Перенос теплоты при конвекции осуществляется перемешивающимися объемами жидкой или газообразной среды, при этом передача теплоты конвекцией сопровождается теплопроводностью.

При движении среды встречаются два вида потока. В потоке первого вида все частицы среды движутся по параллельным траекториям, и их движение длительное время совпадает с направлением всего потока. Движение такого рода называется ламинарным. Второй вид потока называется турбулентным. В нем постоянно происходит перемешивание слоев и каждая частица, находящаяся в таком потоке, перемещаясь вдоль потока, совершает различные движения относительно стенок канала.

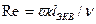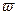Характер движения среды в канале произвольного сечения определяется безразмерной величиной, называемой числом Рейнольдса и равной , где - средняя скорость движения среды, м/с; - эквивалентный диаметр, м; 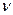- коэффициент кинематической вязкости, м²/с.

При поток в трубопроводе остается ламинарным.

Характер движения среды оказывает влияние на интенсивность теплопередачи. При ламинарном режиме и отсутствии естественной конвекции теплота в перпендикулярном к стенке направлении передается только за счет теплопроводности. И ее количество зависит от физических свойств среды, размеров и формы поверхности канала и почти не зависит от скорости движения среды. При турбулентном движении перенос теплоты к стенкам канала осуществляется конвекцией и теплопроводностью.

В качестве теплоносителей используются различные вещества: воздух, вода, газы, масла, расплавы металлов и т.п. При конвективном теплообмене большое значение, помимо коэффициента теплопроводности 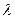, удельной теплоемкости 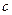, коэффициента температуропроводности 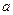, плотности , имеет вязкость среды. Различают динамическую вязкость, характеризуемую силами внутреннего трения между слоями движущейся жидкости, и кинематическую вязкость, равную отношению динамической вязкости к плотности жидкости.

Величина силы трения 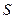между слоями, отнесенная к единице поверхности, согласно закону Ньютона пропорциональна градиенту скорости 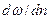по нормали к направлению движения потока: 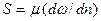, где 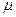- коэффициент динамической вязкости (коэффициент внутреннего трения), Н∙с/м². С увеличением 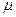вязкость жидкостей возрастает, у капельных сред вязкость уменьшается с увеличением температуры и почти не зависит от давления, у газов вязкость возрастает при увеличении температуры и давления.

Кинематический коэффициент вязкости , м²/с.

Теоретический анализ задач конвективного теплообмена основывается на использовании теории пограничного слоя Л. Прандтля. При омывании какого-либо тела безграничным потоком жидкости с постоянной скоростью течения в непосредственной близости от поверхности тела скорость течения падает до нуля. Тонкий слой вблизи поверхности, в котором происходит изменение скорости от скорости потока вдали от стенки до нуля на стенке, называется пограничным динамическим слоем. Толщина этого слоя увеличивается с увеличением динамической вязкости и уменьшается с увеличением скорости потока жидкости. Характер течения в пограничном слое определяется величиной числа .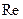

При тепловом воздействии, когда температуры стенки и жидкости неодинаковы, вблизи стенки возникает еще и тепловой пограничный слой. Соотношение толщин динамического и теплового пограничных слоев определяется величиной безразмерного числа 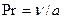. Так, для вязких жидкостей с низкой теплопроводностью (масел) 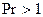и толщина динамического слоя больше толщины теплового пограничного слоя. Для газов 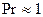и толщины слоев примерно равны.

В случае турбулентного динамического пограничного слоя непосредственно у стенки имеется тонкий слой жидкости, движение в котором является ламинарным. Этот слой называется ламинарным (вязким) подслоем.

При конвективном теплообмене механизм теплоотдачи определяется во многом характером течения. Процесс переноса теплоты на границе с поверхностью определяется законом Фурь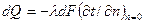е , где - нормаль к поверхности тела. Это же количество может быть выражено уравнением Ньютона-Рихмана 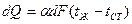. Приравняв правые части обоих уравнений, получим 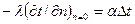. Это уравнение описывает процесс теплообмена на поверхности канала (.

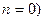Конвективный теплообмен зависит от значительного числа факторов, определяющих процесс теплоотдачи и в общем случае является функцией физических параметров жидкости, характера и скорости ее течения, формы и размеров тела и т.п., т.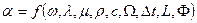е. , где 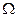- характер движения жидкости, 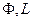- форма и размеры поверхности соответственно.

Дифференциальные уравнения для конвективного теплообмена учитывают как тепловые, так и динамические явления процесса. Система уравнений состоит из уравнений энергии (теплопроводности), теплообмена, движения и сплошности.

При определении величины теплового потока необходимо знать значение температуры, которая в большинстве случаев распределяется неравномерно по сечению канала и по его длине. Поэтому при теоретических исследованиях под температурой понимают среднюю температуру, например, при небольших изменениях температуры потока средняя температура равна 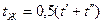, где - средняя температура жидкости у входа в канал, 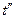- тоже у выхода

Для определения коэффициента теплоотдачи в расчет принимают среднюю скорость жидкости 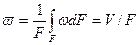, где 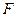- площадь поперечного сечения канала, м²; 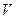- объемный расход жидкости, м³/с; 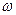- скорость жидкости в каждом элементе сечения .

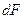При проведении инженерных расчетов для каналов некруглого сечения вместо диаметра принимается так называемый эквивалентный диаметр, равный , где 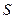- полный (смоченный) периметр сечения. При поперечном обтекании трубы или пучка труб за определяющий размер берется наружный диаметр трубы, а при обтекании плоскости – ее длина по направлению движения потока

Теплообмен при ламинарном течении жидкости в трубе. Формирование характера потока в трубе происходит на начальном ее участке. При входе скорости по сечению распределяются равномерно. Дальше происходит образование гидродинамического пограничного слоя, толщина которого постепенно увеличивается. Стабилизированное течение, характерное для данного режима течения наступает как для ламинарного, так и для турбулентного течения примерно на длине равной .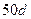

Теплоотдача при течении жидкости в трубе неодинакова по длине, поэтому кроме участка стабилизированного течения устанавливается участок тепловой стабилизации.

При ламинарном изотермном течении жидкости скорости по сечению потока на расстоянии 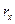от оси трубы распределяются по парабол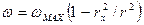е , где 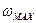- скорость жидкости на оси трубы (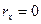), 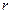- радиус трубы.

Средняя скорость при ламинарном сечении .

При ламинарном течении могут быть два режима неизотермного движения:

- вязкостный режим, соответствующий течению вязких жидкостей при отсутствии естественной конвекции. При этом режиме передача теплоты к стенкам канала осуществляется только теплопроводностью. Распределение скоростей по сечению не будет чисто параболическим, поскольку с изменением температуры будет изменяться и вязкость;

- вязкостно-гравитационный режим имеет место, когда вынужденное течение жидкости сопровождается естественной конвекцией. В этом случае теплота передается теплопроводностью и конвекцией. При вязкостно-гравитационном режиме большое значение оказывает направление свободной конвекции и вынужденного движения. При совпадении направления свободной конвекции и вынужденного движения скорость жидкости у стенки возрастает и теплоотдача увеличивается, в противном случае – наоборот. При взаимно перпендикулярном движении естественной и вынужденной конвекций теплоотдача увеличивается за счет лучшего перемешивания.

Аналитическое исследование теплоотдачи при ламинарном режиме пока не нашло окончательного разрешения и при определении коэффициента теплоотдачи используют эмпирические зависимости:

- при вязкостном режиме средний коэффициент теплоотдачи в прямых гладких трубах определяется по формуле ;

- при вязкостно-гравитационном режиме средний коэффициент теплоотдачи в прямых гладких трубах .

После определения числа Нуссельта коэффициент теплоотдачи определяется по формуле 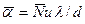, где за определяющую температуру взята средняя температура жидкости, а за определяющий размер диаметр трубы. Эти формулы дают среднее значение коэффициента теплоотдачи при и использовании любой жидкости.

Пример: Требуется определить коэффициент теплоотдачи и количество переданной теплоты при течении воды в горизонтальной трубке диаметром 8 мм и длиной 500 мм, если скорость воды 0,1 м/с, температура воды 80⁰, температура стенки трубки 20⁰С.

При 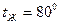C 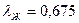Вт/(м∙град), м²/с, 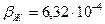1/град, число Прандтля 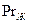= 2,21, 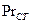= 7,02 при .

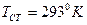Имеем

; .

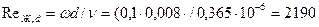Температурный напор 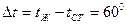С.

Число Грасгофа .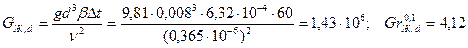

Находим

Коэффициент теплоотдачи Вт/(м²∙град).

Поправка на длину трубы не требуется, так как .

Количество передаваемой теплоты через трубу

Вт.

Теплообмен при турбулентном движении жидкости в трубах. Сложное строение потока при турбулентном движении жидкости в трубе с ламинарным подслоем, представляющим термическое сопротивление, затрудняет аналитическое описание процесса теплообмена. Распределение скоростей по сечению имеет вид усеченной параболы: наиболее резко скорость потока изменяется около стенки в пределах пограничного слоя и более полого в средней части сечения.

В практических расчетах используют средние скорости 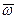. При турбулентном режиме при изотермном течении отношение средней скорости к максимальной является функцией числа Рейнольдса Поскольку при турбулентном режиме происходит интенсивное перемешивание, то естественная конвекция не оказывает практического влияния на теплоотдачу. Поэтому из совокупности чисел подобия исключается число Грасгофа.

При нагревании жидкости интенсивность теплоотдачи выше, чем при охлаждении, что учитывается отношением .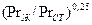

Средний коэффициент теплоотдачи при турбулентном движении () и определяется как 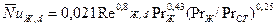. Формула справедлива при .

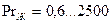При турбулентном движении в изогнутых трубах и змеевиках возникает вследствие центробежного эффекта вторичная циркуляция, что приводит к увеличению коэффициента теплоотдачи и учитывается соответствующим поправочным коэффициентом.

Теплообмен при поперечном обтекании трубы. Безотрывное обтекание поверхности трубы потоком наблюдается при малых значениях числа 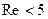. При больших значениях 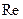ламинарный пограничный слой на лобовой части трубы отрывается от ее поверхности и за кормовой частью образует два симметричных вихря. Поэтому примерно 45 % поверхности трубы омывается безотрывно ( 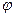= 80…85⁰), а остальная часть находится в вихревой зоне. Чем больше скорость потока, тем при больших углах происходит отрыв ламинарного пограничного слоя.

В лобовой части трубы при 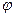= 0 коэффициент теплоотдачи имеет наибольшее значение, так как пограничный слой имеет здесь наименьшую толщину. По мере движения жидкости толщина слоя увеличивается и достигает максимального значения у экватора, примерно в месте отрыва пограничного слоя. За экватором кормовая часть трубы обтекается жидкостью с вихревым характером движения, что способствует разрушению пограничного слоя и ведет к увеличению коэффициента теплоотдачи.

Теплоотдача по окружности трубы при поперечном обтекании связана с характером обтекания ее поверхности и зависит от скорости и направления потока жидкости, температуры и диаметра трубы, направления теплового потока и других внешних элементов, изменяющих степень турбулизации потока и аналитически трудно разрешима. Поэтому в исследовательской практике средний коэффициент теплоотдачи по окружности трубы определяют из уравнения подобия:

При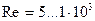

.

При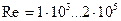

.

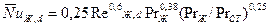При угле атаки меньше 90⁰, то подсчитанный для 90⁰ средний коэффициент теплоотдачи умножается на поправочный коэффициент .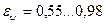

Теплообмен при поперечном обтекании пучка труб. Теплообменные аппараты, содержащие пучки круглых труб, обтекаемые поперечным потоком жидкости, имеют в пищевой промышленности широкое распространение. В теплообменных аппаратах используются в основном два вида установки труб в решетках: коридорный и шахматный.

Характеристиками пучка труб являются: внешний диаметр, число рядов труб по движению потока, относительные шаги по вертикали и горизонтали. В теплообменных аппаратах наблюдается в основном турбулентное течение жидкости. При обтекании первого ряда труб независимо от вида их расположения в решетке режим движения практически не отличается от обтекания одиночной трубы и зависит только от начальной турбулентности потока. При обтекании следующих рядов характер изменяется. Так, при коридорном расположении последующий ряд труб закрывается предыдущим, что ухудшает обтекание лобовой части, и большая поверхность труб находится в слабой вихревой зоне. При шахматном расположении труб коэффициент теплоотдачи при прочих равных условиях выше, чем при коридорном их расположении.

При коридорном расположении труб теплоотдача, как в лобовой, так и в кормовой частях труб будет меньшей, чем при обтекании одиночной трубы. Поскольку каждый ряд вызывает дополнительную турбулизацию, то коэффициент теплоотдачи для второго ряда будет выше, чем для первого, а для третьего выше, чем для второго. После третьего ряда происходит стабилизация потока жидкости и коэффициент теплоотдачи для остальных рядов примерно постоянен.

При расчете теплообменных аппаратов для определения среднего коэффициента теплоотдачи третьего ряда труб применяются следующие уравнения подобия:

При коридорном расположении труб в решетке

;

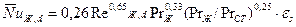При шахматном расположении труб

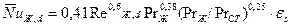, где - поправочный коэффициент для глубинных рядов пучка, выбираемый в зависимости от отношения .

Значение коэффициента теплоотдачи для труб первого ряда определяется умножением коэффициента теплоотдачи для третьего ряда на поправочный коэффициент 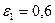, для труб второго ряда на 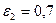(для коридорного расположения труб ).

Среднее значение коэффициента теплоотдачи для всего пучка подсчитывается по формуле , где 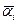- средние коэффициенты теплоотдачи в отдельных рядах труб, - поверхности нагрева каждого ряда.

Если пучок обтекается потоком, направленным под углом меньшим 90⁰, то коэффициент теплоотдачи умножается на поправочный коэффициент .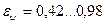

Теплообмен при свободном движении. Конвективный теплообмен в свободном потоке возникает от изменения плотности жидкости или газа при нагревании. Свободная конвекция наблюдается, например, в холодильных камерах при охлаждении продуктов, у нагретых поверхностей печей и сушилок, у батарей отопления и т.д.

Возникающее свободное движение может быть ламинарным или турбулентным. Характер движения зависит в основном от температурного напора , где - температура нагретой поверхности, 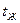- температура неподвижной жидкости вдали от поверхности.

Аналитические решения задач по определению теплоотдачи при свободном ламинарном или турбулентном движении получены при целом ряде упрощающих допущений и поэтому широкого практического использования не получили. Определение коэффициента теплоотдачи осуществляется в основном экспериментальным путем.

Для определения средних коэффициентов теплоотдачи при свободном ламинарном движении жидкости вдоль вертикальных стенок используется следующее эмпирическое уравнение подобия:

При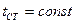

.

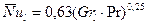При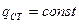

.

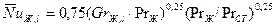Формулы получены для теплоносителей с числом Прандтля от 0,7 до и ими можно пользоваться при

Средний коэффициент теплоотдачи при турбулентном движении жидкости вдоль вертикальной стенки определяется из уравнения подобия

.

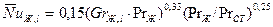Для определения средних коэффициентов теплоотдачи при свободном ламинарном движении жидкости около горизонтальных труб используется выражение .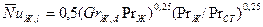

Пример: Требуется определить передачу теплоты при свободной конвекции от вертикального трубопровода диаметром 120 мм и высотой 2,5 м к воздуху при температуре стенки 520⁰К и воздуха 293⁰К.

При температуре окружающей среды 293⁰К имеем Вт/(м∙град), м²/с.

Число Грасгофа

При этих условиях движение воздуха турбулентно.

= …

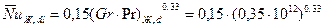Коэффициент теплоотдачи = …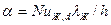

Потери теплоты трубопроводом 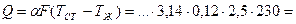…Вт.

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: