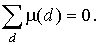Пункт 14. Примеры мультипликативных функций.

Предыдущий пункт дал нам общие абстрактные знания о мультипликативных функциях вообще. Благодаря этому, в этом пункте мы сможем во всеоружии встретить целую серию примеров полезных мультипликативных функций. Большинство этих примеров строятся с использованием лемм предыдущего пункта, а в качестве исходного строительного материала берется какая-нибудь конкретная степенная функция q (а) = а ^s , которая, конечно, мультипликативна. Вы готовы? Начинаем.

Пример 1. Число делителей данного числа.

Пусть q (а) = а ⁰ º 1 - тождественная единица (заведомо мультипликативная функция). Тогда, если

,

то тождество леммы 1 пункта 13 принимает вид:

,

- это не что иное, как количество делителей числа a. По лемме 2 пункта 13, количество делителей t (a) числа a есть мультипликативная функция.

Численный примерчик. t (720) = t (2 ⁴ · 3 ² · 5) = (4 + 1)(2 + 1)(1 + 1) = 30.

Пример 2. Сумма делителей данного числа.

Пусть q (a) = a ¹ º a - тождественная мультипликативная функция. Тогда, если

,

то тождество леммы 1 пункта 13 принимает вид:

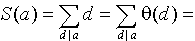
сумма первых (a + 1) членов геометрической прогрессии

- сумма всех делителей числа a. По лемме 2 пункта 13, сумма всех делителей есть мультипликативная функция.

Численный примерчик.

S (720) = S (2 4 · 3 2 · 5) =

2 5 - 1 2 - 1

·

3 3 - 1 3 - 1

·

5 2 - 1 5 - 1

= 2418.

Пример 3. Функция Мебиуса.

Функция Мебиуса m (a) - это мультипликативная функция, определяемая следующим образом: если p - простое число, то m (p) = -1; m (p a) = 0, при a > 1; на остальных натуральных числах функция доопределяется по мультипликативности.

Таким образом, если число a делится на квадрат натурального числа, отличный от единицы, то m (a) = 0; если же a = p ₁ p _{2· · ·} p _n (теоретик-числовик сказал бы на своем жаргоне: "если a свободно от квадратов"), то m (a) = (-1) ^k , где k - число различных простых делителей a. Понятно, что m (1) = (-1) ⁰ = 1, как и должно быть.

Лемма 1. Пусть q (a) - произвольная мультипликативная функция,

.

Тогда:

(при a = 1 считаем правую часть равной 1).

Доказательство. Рассмотрим функцию q ₁ (x) = m (x) · q (x). Эта функция мультипликативна, как произведение мультипликативных функций. Для q ₁ (x) имеем (p - простое): q ₁ (p) = - q (x); q ₁ (p a) = 0, при a > 1. Следовательно, для q ₁ (x) тождество леммы 1 пункта 13 выглядит так:

¨

Следствие 1. Пусть q (d) = d ^-1 = 1/ d (это, конечно, мультипликативная функция),

Тогда:

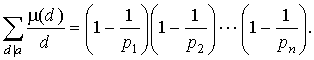
Воздержусь от доказательства этого следствия в силу банальности сего доказательства, но вот на правую часть этого тождества попрошу обратить внимание, так как она еще неоднократно у нас встретится. Физический смысл этой правой части раскрывает пример следующей функции.

Пример 4. Функция Эйлера.

Функция Эйлера, пожалуй, самая знаменитая и "дары приносящая" функция из всех функций, рассматриваемых в этом пункте. Функция Эйлера j (a) есть количество чисел из ряда 0, 1, 2,..., a - 1, взаимно простых с a. Полезность и практическое применение этой функции я продемонстрирую в следующих пунктах, а сейчас давайте поймем, как ее вычислять.

Лемма 2. Пусть

.

Тогда:

1) (формула Эйлера);

2)

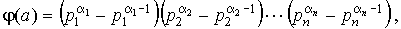
в частности, j (p ^a ) = p ^a - p ^{a -1} , j (p) = p - 1.

Доказательство. Пусть x пробегает числа 0, 1, 2,..., a - 1. Положим d _x = (x, a) - наибольший общий делитель. Тогда j (a) есть число значений d _x , равных 1. Придумаем такую функцию c (d _x ), чтобы она была единицей, когда d _x единица, и была нулем в остальных случаях. Вот подходящая кандидатура:

Последнее легко понять, если вспомнить лемму 1 из этого пункта и в ее формулировке взять q (d) º 1. Далее, сделав над собой некоторое усилие, можно усмотреть, что:

Поскольку справа сумма в скобках берется по всем делителям d числа d _x = (x, a), то d делит x и d делит a. Значит в первой сумме справа в суммировании участвуют только те x, которые кратны d. Таких x среди чисел 0, 1, 2,..., a - 1 ровно a / d штук. Получается, что:

что и требовалось.

Пояснение для читателей, у которых предыдущие соображения не захотели укладываться в голову, например, из-за плохих погодных условий. Имеем

Зафиксируем некоторое d ₀ такое, что d ₀ делит a, d ₀ делит x, x < a. Значит в сумме справа в скобках слагаемых m (d ₀ ) ровно a / d ₀ штук и j (a) есть просто сумма

После этого, равенство

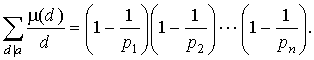
получается применением следствия из леммы 1 этого пункта. Должен признать, что приведенное доказательство формулы Эйлера и, в особенности, его последний момент с изменением порядка суммирования, объективно тяжеловаты для понимания. Но мы не боимся трудностей!

Второе утверждение леммы следует из первого внесением впереди стоящего множителя a внутрь скобок.

¨

Оказывается, только что доказанная формула

для вычисления функции Эйлера имеет ясный "физический смысл". Дело в том, что в ней отражено так называемое правило включений и исключений:

Правило включений и исключений. Пусть задано множество А и выделено k его подмножеств. Количество элементов множества А, которые не входят ни в одно из выделенный подмножеств, подсчитывается так: надо из общего числа элементов А вычесть количества элементов всех k подмножеств, прибавить количества элементов всех их попарных пересечений, вычесть количества элементов всех тройных пересечений, прибавить количества элементов всех пересечений по четыре и т.д. вплоть до пересечения всех k подмножеств.

Проиллюстрирую это правило на примере подсчета функции Эйлера для чисел вида

Посмотрите на рисунок 4.

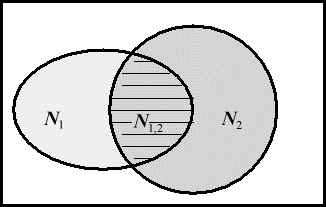
Рис. 4.

Прямоугольник изображает множество всех целых чисел от 0 до a; овал N ₁ - множество чисел, кратных p ₁ ; кружок N ₂ - числа, кратные p ₂ ; пересечение N _1,2 - множество чисел, делящихся одновременно на p ₁ и p ₂ , т.е. на p ₁ p ₂ ; числа вне овала и кружочка взаимно просты с a. Для подсчета числа чисел, взаимно простых с a, нужно из a вычесть количество чисел в N ₁ и количество чисел в N ₂ (их, соответственно, a / p ₁ и a / p ₂ штук), при этом общая часть N _1,2 (там a /(p ₁ p ₂ ) штук чисел) вычтется дважды, значит ее надо один раз прибавить (вот оно, "включение - исключение"!). В результате получим:

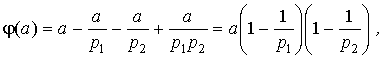
что я вам и утверждал. Мне кажется, что таким способом можно объяснить формулу Эйлера любому смышленому школьнику.

Кстати, любому смышленому школьнику вполне возможно объяснить и то, что при a > 2, j (a) всегда число четное. Действительно, если k взаимно просто с a и k < a, то число a - k тоже меньше a, взаимно просто с a и не равно k. (Если бы a и a - k имели общий делитель, то их разность a - (a - k) = k тоже делилась бы на этот делитель, что противоречит взаимной простоте a и k.) Значит числа, взаимно простые с a разбиваются на пары k и a - k, следовательно, их четное число.

Из леммы 2 вытекают приятные следствия.

Следствие 2. Функция Эйлера мультипликативна.

Доказательство. Имеем:

- произведение двух мультипликативных функций, первая из которых мультипликативна по лемме 2 пункта 13. Значит, j (a) - мультипликативна.

¨

Следствие 3. .

Доказательство. Пусть

.

Тогда, по лемме 1 пункта 13 имеем:

.

¨

Численные примерчики.

j (5) = 5 - 1 = 4

j (30) = j (2 · 3 · 5) = (2 - 1)(3 - 1)(5 - 1) = 8

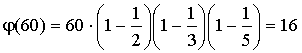
На этом, пожалуй, пункт 14 закончим. Кроме того, предложение, которое вы сейчас начали внимательно читать, тоже закончилось.

Задачки

1. Потренируйтесь и найдите число делителей и сумму делителей чисел: а) 5600; б) 116424. 2. Найдите сумму собственных делителей (т.е. делителей, отличных от самого числа) чисел: а) 6; б) 28; в) 496; г) 8128. Подивитесь полученному результату. (1) 3. Составьте таблицу значений функции Мебиуса m (n) для всех значений n от 1 до 100. Бережно сохраните результат. 4. Составьте таблицу значений функции Эйлера j (n) для всех значений n от 1 до 100. Бережно сохраните результат. 5. Используя формулу Эйлера для j (n), еще раз докажите бесконечность множества простых чисел. 6. Докажите, что существует бесконечно много чисел n Î N, удовлетворяющих для всех k = 1, 2,..., n - 1 неравенствам S (n) n > S (k) k , где S (n) - сумма всех делителей числа n. 7. Докажите, что для любого натурального n выполняются неравенства n 2 < j (n) · S (n) < n 2 . 8. На кафтане площадью 1 нашито 5 заплат, площадь каждой из которых не меньше 1/2. Докажите, что найдутся две заплаты, площадь общей части которых не меньше 1/5. 9. Элитарный бизнес-клуб регулярно посещают 220 новых русских. При бизнес-клубе имеется шесть спортивных секций, представляющие следующие виды спорта: глазопучинг, разглядывание тяжестей, прыжки в ширину, дебилдинг, бег в трусцах, футбол ежом. В эти секции записались, соответственно, 30, 26, 32, 31, 28 и 36 человек. В несколько секций записались 53 новых русских, из них 24 братана посещают три или больше секций, 9 братанов не меньше четырех секций и 3 братана - даже пять секций. В последнюю тройку братанов входит один чудак, который записался во все шесть секций. Директор клуба хочет знать, сколько братанов не записались ни в одну секцию? 10. Пусть k - натуральное число, d пробегает все делители числа а с условием j (d) = k. Докажите, что 11. Пусть k - четное натуральное число, d пробегает все делители свободного от квадратов числа a = p 1 p 2· · · p k с условием 0 < d < Ö a. Докажите, что

(1) Числа равные сумме собственных делителей древние греки назвали совершенными. В формулировке задачи указаны первые четыре (известных еще Пифагору) совершенных числа. Евклид обнаружил, что если число 2 ^k -1 - простое, то число (2 ^k -1) · 2 ^{k -1} обязано быть совершенным. Эйлер доказал, что все четные совершенные числа имеют такой вид. Неизвестно, существуют ли вообще нечетные совершенные числа; во всяком случае, такие числа должны быть больше 10 ¹⁰⁰ - результат хорошо организованной машинной проверки. Имеется ровно 24 значения k < 20000, для которых число 2 ^k -1 - простое (в этом случае k само обязано быть простым). Простые числа вида 2 ^k -1 называются числами Мерсенна, по имени французского математика, который в 1644 году указал в большей части верный список всех таких простых, меньших 10 ⁷⁹ . Изрядно потрудившись, читатель сам может выписать наибольшее известное на сегодняшний день совершенное число, отталкиваясь от наибольшего известного на сегодня простого числа Мерсенна, указанного в пункте 6 этой книжки. Предполагается, что совершенные числа были известны уже в древнем Вавилоне и Египте, где рука с загнутым безымянным пальцем обозначала число шесть - первое совершенное число. Тем самым этот палец сам стал причастен к совершенству и за ним закрепилась привилегия носить обручальное кольцо.

Пункт 15. z -функция Римана.

Этот пункт несколько сложнее предыдущих, так как для его понимания потребуются определенные знания из области математического анализа и теории функций комплексного переменного. Но было бы просто неправильно в параграфе под названием "Важнейшие функции в теории чисел" умолчать об одной из самых загадочных и влиятельных в математике функций - z -функции Римана, поэтому сделаем над собой некоторое усилие, отбросим внутреннюю скованность и попытаемся подойти к z -функции, чтобы познакомиться (надеюсь, более обстоятельно, чем с симпатичной девушкой, бегущей на автобус по суетливой улице). Всюду ниже буквой C обозначается поле комплексных чисел.

Определение. Пусть s Î C, действительная часть Re(s) > 1. z -функцией Римана называется функция комплексного переменного, задаваемая рядом:

Правомерность такого определения подтверждает следующее наблюдение.

Наблюдение. В полуплоскости Re(s) > 1 ряд
сходится абсолютно.

Доказательство. Пусть s Î C, Re(s) > 1, s = s + i j (cм. рис. 5).

Рис. 5.

Посчитаем абсолютные величины членов ряда:

Теперь воспользуемся интегральным признаком сходимости (мы помним, что s > 1):

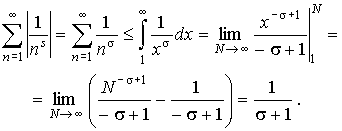
Значит, при s > 1 ряд
сходится абсолютно.

¨

Из этого наблюдения вытекает

Следствие 1. Функция z (s) аналитична в полуплоскости Re(s) > 1.

Доказательство. Действительно, при всяком e > 0 и фиксированном r > 1+ e, числовой ряд 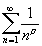мажорирует ряд из абсолютных величин = 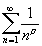, где s ³ r, откуда, по теореме Вейерштрасса, следует равномерная сходимость ряда в полуплоскости Re(s) ³ r. Сумма же равномерно сходящегося ряда из аналитических функций сама является аналитической функцией.

Теперь осталось только неограниченно приближаться к вертикальной пунктирной прямой Re(s) = 1 на рис.5, устремляя e к нулю. Получается, что во всех полуплоскостях, граница которых сколь угодно близко подходит к прямой Re(s) = 1, ряд сходится абсолютно и равномерно (почти как лошади на водопой), а его сумма - аналитическая функция.

¨

Нематематическое (значит, лирическое) отступление.

Справедливости ради следует сказать, что функцию впервые рассматривал Эйлер, который узнал много ее свойств и открыл свою знаменитую формулу , связывающую z (s) с простыми числами. Поэтому, правильнее было бы называть главную героиню этого пункта дзета-функцией Эйлера. Однако математики - люди твердолобые, и раз уж так повелось, талдычат все: "дзета-функция Римана" да "дзета-функция Римана". (Ортодоксальные математики до сих пор, например, условия аналитичности Даламбера - Эйлера функции комплексного переменного называют условиями Коши - Римана.) Разумеется, Риман тоже изучал функцию z (s) и высказал про нее много интересного, но мы не будем осуждать здесь ортодоксальных математиков за неправильное именование функции z (s), ибо само по себе имя ярчайшей звезды математического небосклона Георга Фридриха Бернгарда Римана есть вечная награда для любой функции, а z (s) такой орден, несомненно, заслужила.

Несколько слов о Бернгарде Римане (1826 - 1866), человеке, который в очень большой степени определил лицо современной математики. Риман был сыном деревенского священника, учился в Геттингенском университете, где в 1851 году получил степень доктора, в 1854 году стал приват-доцентом, в 1859 году - профессором, переемником Дирихле на кафедре математики. Болезненный, он провел последние несколько месяцев жизни в Италии, где и умер в сорокалетнем возрасте. За свою короткую жизнь Риман опубликовал небольшое число работ, но каждая из них - настоящая жемчужина, открывающая новые и плодотворные области. Именно Риману мы обязаны введением в анализ топологических представлений, понятию римановой поверхности, определению интеграла Римана, исследованию гипергеометрических рядов и абелевых функций, и так далее, и так далее. Именно ему мы обязаны новому взгляду на геометрию, при котором пространство вводится как топологическое многообразие с метрикой, задаваемой произвольной квадратичной дифференциальной формой (теперь мы говорим - римановы пространства). В работе 1859 года он исследовал количество простых чисел, меньших заданного числа, и дал точную формулу для нахождения этого числа с участием функции z (s). В этой знаменитой работе сформулирована не менее знаменитая "Гипотеза Римана" о нулях аналитического продолжения z (s) на всю комплексную плоскость (Верно ли, что все не действительные нули дзета-функции лежат на прямой Re(s) =1/2?). Эта гипотеза, пожалуй, является одной из самых старых, трудных и насущных математических проблем. Она до сих пор не доказана и не опровергнута. Слава Богу, что ее формулировка неэлементарна, а то многочисленные доморощенные математики-ферматисты кинулись бы ее доказывать и одному из сотрудников математико-механического факультета Уральского госуниверситета пришлось бы, наряду с патологическими доказательствами теоремы Ферма, читать еще и "доказательства" гипотезы Римана, а это было бы уже совершенно невыносимо, так как может спровоцировать у сотрудника поступки суицидального характера.

Далее нам потребуются некоторые сведения из матанализа и теории функций комплексного переменного про бесконечные произведения. Бесконечные произведения - забавная и полезная потеха, которой почему-то, в отличие от бесконечных сумм, на лекциях в университете уделяют мало внимания. Исправим, отчасти, сие недоразумение.

Определение. Пусть u ₁ , u ₂ ,..., u _n ,... - бесконечная последовательность комплексных чисел и все u _j ¹ - 1. Выражение вида:

(ª)

называется бесконечным произведением, а выражения:

- частичными произведениями бесконечного произведения (ª).

Если последовательность частичных произведений v _k при k ® ¥ сходится к числу v ¹ 0, то говорят, что бесконечное произведение (ª) сходится и равно v. В противном случае, если v _k не сходится (или v _{k ®} 0), то говорят, что бесконечное произведение (ª) расходится (соответственно, расходится к нулю).

Честно говоря, при первом знакомстве, словосочетание "расходится к нулю" вызвало у меня недоумение. Однако, при дальнейшем изучении конструкции бесконечного произведения, это недоумение рассеялось, так как выделение особого случая v _{k ®} 0 связано с традицией логарифмировать бесконечные произведения, чтобы перейти к рядам - более знакомым объектам, а логарифм нуля не имеет смысла и, видимо, находится далеко за пределами нашего разумения.

Теорема 1 (Признак сходимости (ª)). Если ряд

u ₁ + u ₂ +... + u _n +...

сходится абсолютно, то бесконечное произведение (ª) сходится.

Доказательство. Пусть 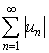- сходится, значит общий член этого ряда стремится к нулю и можно считать, что, например, | u _n | £ 1/2 для всех n > n _{0 Î} N. Пусть сначала u _{n Î} R. Тогда, в силу замечательного предела , начиная с некоторого номера n > n ₀ , имеем: |ln (1 + u _n )| £ 2| u _n |. Значит последовательность логарифмов частичных произведений

Sn = ln (1 + u ₁ ) + ln (1 + u ₂ ) +…+ ln (1 + u _n ) = ln v _n

сходится, т.к. , а справа в последнем неравенстве стоят частичные суммы сходящегося ряда. Следовательно, сходится и бесконечное произведение (ª).

Пусть теперь u _n - произвольные комплексные числа. Надо доказать, что при n ® ¥ сходятся две последовательности действительных чисел:

| v _n | = |(1+ u ₁ ) ·...· (1+ u _n )| = |1+ u ₁ | ·...· |1+ u _n | (1)

arg v _n = arg ((1+ u ₁ ) ·...· (1+ u _n )) = arg (1+ u ₁ ) +...+ arg (1+ u _n ) (2)

Пусть u _n = a _n + i b _n . Ясно, что для сходимости последовательности

| v _n | необходимо и достаточно сходимости последовательности | v _n | ² .

Но |1+ u _n | ² = |1 + a _n + i b _n | ² = 1 + a _n ² + b _n ² + 2 a _n и, так как

| a _n ² + b _n ² + 2 a _n | £ | u _n | ² + 2| u _n |, то сходимость (1) следует из уже доказанного. Сходимость (2) следует из того, что при всех n, больших некоторого n ₀ , | arg (1+ u _n)| = (здесь опять использован замечательный предел
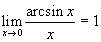), а | b _n | ® 0 т.к. u _n ® 0.

¨

Ключ к пониманию огромной роли функции z (s) в теории чисел кроется в уже упоминавшейся выше замечательной формуле Эйлера.

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: