 |
Пункт 13. Мультипликативные функции.
|
|
|
|
В этом пункте с "чертоводюжинным" номером речь пойдет об одном важном классе функций, которому в теории чисел посвящены целые монографии (см., напр., книжку Г.Дэвенпорта "Мультипликативная теория чисел").
Определение. Функция q: R ® R (или, более общо, q: C ® C) называется мультипликативной если:
1). Функция q определена всюду на N и существует а Î N такой, что q (а) ¹ 0.
2). Для любых взаимно простых натуральных чисел а 1 и а 2 выполняется q (а 1 · а 2 ) = q (а 1 ) · q (а 2 ).
Пример 1. q (а) = а s , где s - любое (хоть действительное, хоть комплексное) число. Проверка аксиом 1) и 2) из определения мультипликативной функции не составляет труда, а сам пример показывает, что мультипликативных функций по меньшей мере континуум, т.е. много.
Перечислим, кое-где доказывая, некоторые свойства мультипликативных функций. Пусть всюду ниже q (а) - произвольная мультипликативная функция.
Свойство 1. q (1) = 1.
Доказательство. Пусть а - то самое натуральное число, для которого q (а) ¹ 0. Тогда q (а · 1) = q (а) · q (1) = q (а).
¨
Свойство 2.
,
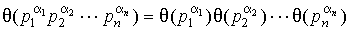где р 1 , р 2 ,..., р n - различные простые числа.
Доказательство очевидно.
¨
Свойство 3. Обратно, мы всегда построим некоторую мультипликативную функцию q (a), если зададим q (1) = 1 и произвольно определим q (р a) для всех простых р и всех натуральных a, а для остальных натуральных чисел доопределим функцию q (a) используя равенство
.
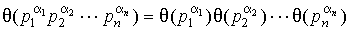Доказательство сразу следует из основной теоремы арифметики.
¨
Пример 2. Пусть q (1) = 1 и q (р a) = 2 для всех р и a. Тогда, для произвольного числа,
.
Свойство 4. Произведение нескольких мультипликативных функций является мультипликативной функцией.
Доказательство. Сначала докажем для двух сомножителей: Пусть q 1 и q 2 - мультипликативные функции q = q 1 · q 2 , тогда (проверяем аксиомы определения)
|
|
|
1) q (1) = q 1 (1) · q 2 (1) = 1 и, кроме того, существует такое a (это a = 1), что q (a) ¹ 0.
2) Пусть (a, b) = 1 - взаимно просты. Тогда
q (a · b) = q 1 (a · b) · q 2 (a · b) =
= q 1 (a) q 1 (b) q 2 (a) q 2 (b) =
= q 1 (a) q 2 (a) · q 1 (b) q 2 (b) = q (a) q (b).
Доказательство для большего числа сомножителей проводится стандартным индуктивным рассуждением.
¨
Введем удобное обозначение. Всюду далее, символом
будем обозначать сумму чего-либо, в которой суммирование проведено по всем делителям d числа n. Следующие менее очевидные, чем предыдущие, свойства мультипликативных функций я сформулирую в виде лемм, ввиду их важности и удобства дальнейших ссылок.
Лемма 1. Пусть
- каноническое разложение числа a Î N, q - любая мультипликативная функция. Тогда:
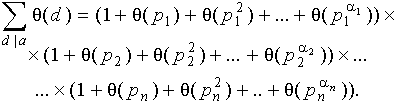
Если a = 1, то считаем правую часть равной 1.
Доказательство. Раскроем скобки в правой части. Получим сумму всех (без пропусков и повторений) слагаемых вида
,
где 0 £ b k £ a k , для всех k £ n. Так как различные простые числа заведомо взаимно просты, то
,
а это как раз то, что стоит в доказываемом равенстве слева.
¨
Лемма 2. Пусть q (a) - любая мультипликативная функция. Тогда
,
- также мультипликативная функция.
Доказательство. Проверим для c (a) аксиомы определения мультипликативной функции.
1). 
2). Пусть
и все р и q различны. Тогда, по предыдущей лемме, имеем: (благо, делители у чисел a и b различны)
¨
Итак, я перечислил шесть свойств мультипликативных функций, которые пригодятся нам в дальнейшем. Просьба хорошенько их запомнить и не унывать даже в самой тяжелой жизненной ситуации.
Задачки 
| 1. Предлагаю читателю самостоятельно доказать обратное утверждение к лемме 2 настоящего пункта, а именно, если
- мультипликативная функция и функция q (n) всюду определена хотя бы на N, то q (n) также обязана быть мультипликативной функцией.
2. Пусть q (p a) = a для всех простых р. Вычислите
а) q (864); б) q (49500).
3. Пусть q (p a) = a для всех простых р. Вычислите
|
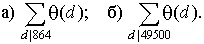
| 4. Пусть вещественная мультипликативная функция f (x) определена и непрерывна для всех x > 0. Докажите, что f (x) = x s для некоторого s Î R, т.е. примером 1 настоящего пункта исчерпываются все непрерывные мультипликативные функции. (1) |
(1) Самым первым на планете Земля этот факт установил О. Коши, интересовавшийся решениями функциональных уравнений следующих четырех видов:
|
|
|
f (a + b) = f (a) + f (b); f (a + b) = f (a) f (b);
f (ab) = f (a) + f (b); f (ab) = f (a) f (b).
Он установил, что непрерывные решения этих уравнений имеют, соответственно, вид (в классе разрывных функций могут быть и другие решения):
Cx; e Cx ; C ln x; x C (x > 0).
|
|
|
