 |
Пункт 11. Еще кое-что о цепных дробях (приближение чисел, периодичность, теорема Эрмита).
|
|
|
|
В этом пункте я хочу рассказать кое-что еще о свойствах цепных дробей, что не уложилось в схему рассказа предыдущих четырех пунктов. Прежде всего это следующая замечательная теорема, показывающая, что среди всех рациональных дробей с ограниченным по величине знаменателем, наилучшим образом приближает произвольное число именно его подходящая дробь.
Теорема. Пусть a - произвольное число, s > 1, а если при этом
a = a / b - несократима, то s < n, где n таково, что Q n = b. Тогда неравенство
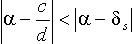
возможно только если у несократимой дроби c / d знаменатель больше Q s .
Доказательство. Мы знаем, что a всегда лежит между соседними подходящими дробями, поэтому всегда
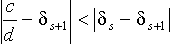
Это неравенство проиллюстрировано рисунком 4, разглядывая который, нужно помнить, что
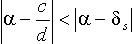
(тогда иллюстрируемое неравенство становится очевидным, даже если c / d < d s +1 ).
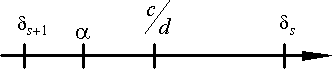
Рис. 4
Из проиллюстрированного неравенства следует, что
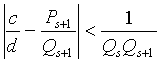
и, если c / d ¹ d s +1 , то
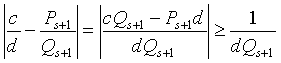
Следовательно,
| dQ s +1 | < | Q s Q s +1 |
и, значит, d > Q s , что и требовалось. Если же c / d = d s +1 , то d = Q s +1 > Q s .
¨
Итак, подходящая дробь - наилучшее приближение данного числа среди всех дробей, знаменатели которых не превосходят знаменатель подходящей дроби. Здесь мы вплотную подошли к вопросу о приближении произвольных чисел рациональными дробями. Оказывается, что это очень интересная теория, имеющая далеко идущие следствия. Остановимся, однако, здесь до лучших времен наступления параграфа 5 "Трансцендентные числа", где мы снова столкнемся с приближением действительных чисел при изучении их алгебраических свойств. Есть время разбрасывать камни, есть время их собирать.
Обратим теперь наше внимание на внешний вид цепных дробей. Весь жизненный опыт говорит нам, что внешний вид - далеко не последнее дело, особенно если речь идет о представительницах прекрасного пола (в частности, цепных дробях). Иногда по внешнему виду человека можно составить вполне адекватное представление о его внутренней сущности. Так, например, если ко мне на экзамен явился босой студент, засунувший себе в ноздри две большие пуговицы, то у меня возникнут сильные сомнения в его способности сдать экзамен, ведь ему будет трудно дышать. Кроме того, он будет мешать остальным, так как его волосатые ноги, скорей всего, будут привлекать всеобщее внимание. Внешний вид математического объекта также может многое поведать о внутренних свойствах. Мы знаем, например, что любая периодическая десятичная дробь (периодичность - это "внешний вид") обязательно представляет собой некоторое рациональное число (рациональность - это "внутреннее свойство") и наоборот. Попытаемся взглянуть с подобной точки зрения на цепные дроби и зададимся вопросом - какие числа представимы в виде периодической цепной дроби?
|
|
|
Определение. Бесконечная цепная дробь
называется периодической, если для последовательности q 1 , q 2 ,..., q n ,... ее неполных частных найдутся такие натуральные k 0 и h, что для любого k ³ k 0 выполнено q k+h = q k , т.е. последовательность неполных частных, начиная с некоторого места k 0 периодическая.
Определение. Иррациональное число, являющееся корнем некоторого квадратного уравнения с целыми коэффициентами, называется квадратичной иррациональностью.
Примеры квадратичных иррациональностей:
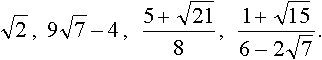
Примеры не квадратичных иррациональностей:
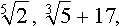
числа p, e и многие другие(пояснения к подобным примерам не квадратичных иррациональностей будут даны в параграфе 5 "Трансцендентные числа").
Теорема (Лагранж). Квадратичные иррациональности и только они представимы в виде бесконечной периодической цепной дроби.
|
|
|
Доказательство. Пусть
- периодическая цепная дробь. Назовем число
остатком цепной дроби a. Таким образом, остаток r n цепной дроби a - это весь ее "хвост" вниз и вправо, начиная с n -ого этажа. Ясно, что
Остатки периодической цепной дроби, очевидно, удовлетворяют соотношению: r k+h = r k , где k ³ k 0 , h - период последовательности неполных частных. Это означает (вспоминаем свойства подходящих дробей), что
| a = | P k -1 r k + P k -2 Q k -1 r k + Q k -2 | = | P k+h -1 r k+h + P k+h -2 Q k+h -1 r k+h + Q k+h -2 | = |
| = | P k+h -1 r k + P k+h -2 Q k+h -1 r k + Q k+h -2 | , |
откуда
| P k -1 r k + P k -2 Q k -1 r k + Q k -2 | = | P k+h -1 r k + P k+h -2 Q k+h -1 r k + Q k+h -2 |
- квадратное уравнение с целыми коэффициентами для нахождения r k . Значит, r k - квадратичная иррациональность, следовательно,
| a = | P k -1 r k + P k -2 Q k -1 r k + Q k -2 |
- тоже квадратичная иррациональность.
Обратное утверждение теоремы доказывается чуть-чуть сложнее. Пусть a удовлетворяет квадратному уравнению с целыми коэффициентами
a a 2 + b a + c = 0. (1)
Разложим a в цепную дробь и подставим в уравнение (1) вместо a его выражение
| a = | P n -1 r n + P n -2 Q n -1 r n + Q n -2 |
через некоторый остаток r n цепной дроби. После преобразований снова получается квадратное уравнение
A n r n 2 + B n r n + C n = 0, (2)
где
- суть целые числа. Видно, что C n = A n -1 . Кроме того, дискриминанты квадратных уравнений (1) и (2) совпадают при всех n:
.
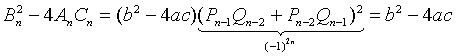Так как (по свойствам подходящих дробей)
,
| то P n -1 = a Q n -1 + | e n -1 Q n -1 | , |
где e n -1 - некоторое подходящее число такое, что | e n -1 | < 1. Теперь, набравшись терпения, посчитаем коэффициент A n в квадратном уравнении (2):
Значит, для любого натурального n,
,
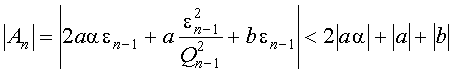| C n | = | A n -1 | < 2 a a +| a | + | b |.
Таким образом, целые коэффициенты A n и C n уравнения (2) ограничены по абсолютной величине и, следовательно, при изменении n могут принимать лишь конечное число различных значений. Так как дискриминанты уравнений (1) и (2) совпадают, то и коэффициент B n может принимать лишь конечное число различных значений. Значит, при изменении n от 1 до ¥, мы повстречаем лишь конечное число различных уравнений вида (2), т.е. лишь конечное число различных остатков r n . Это значит, что некоторые два остатка r n и r n+h с разными номерами обязательно совпадают, что и означает периодичность цепной дроби.
|
|
|
¨
Итак, квадратичные иррациональности и только они представляются периодическими цепными дробями. "Внешний вид" цепных дробей, представляющих иррациональности других типов, в настоящее время науке неизвестен (за очень редкими исключениями), и, по видимому, описание этого внешнего вида является очень сложным вопросом. Некоторые дополнительные замечания о внешнем виде цепных дробей содержатся в пункте 25.
Я хочу закончить весь этот параграф о цепных дробях демонстрацией их применения в изящном и элегантном теоретико-числовом рассуждении, принадлежащем Ш. Эрмиту (1822-1901). Этот эффектный результат представляет собой типичный пример в достаточной степени бесполезного, с точки зрения народного хозяйства, математического утверждения.
Теорема. Всякий делитель числа а 2 + 1, где а Î Z, представим в виде суммы двух квадратов.
Доказательство. Пусть d | (а 2 + 1). Значит d не делит а. Разложим a / d в цепную дробь. Знаменатели ее подходящих дробей образуют возрастающую цепочку: 1 = Q 1 < Q 2 <... < Q n = d. Значит найдется такой номер k Î N, что
Q k £ Ö d £ Q k +1 (ª)
и хоть одно из этих неравенств - строгое. Далее, a / d лежит между соседними подходящими дробями, значит
,
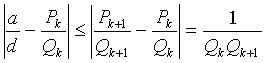т.е.
,
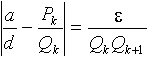где e £ 1. Приведем разность внутри модуля к общему знаменателю:
.
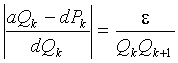Имеем:
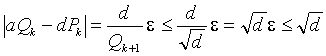
(здесь первое неравенство следует из (ª)), значит (aQ k -dP k ) 2 £ d. Кроме того, из другого неравенства в (ª) следует Q k 2 £ d и хоть одно из двух последних написанных неравенств строгое. Сложив их, получим строгое неравенство:
(aQ k - dP k ) 2 + Q k 2 < 2 d,
т.е.
(a 2 + 1) Q k 2 - 2 adQ k P k + d 2 P k 2 < 2 d.
Слева стоит сумма двух квадратов - целое положительное число (строго больше нуля) и каждое из трех слагаемых слева делится на d. Получается, что левая часть делится на d и строго меньше 2 d, т.е. левая часть есть само число d, и
(aQ k - dP k ) 2 + Q k 2 = d
- сумма двух квадратов.
¨
Финиш одиннадцатого пункта и всего второго параграфа.
Задачки 
| 1. Найдите наилучшее рациональное приближение к числу 971/773 со знаменателем, не превышающим 82, и оцените погрешность приближения.
2. Среди всех рациональных дробей со знаменателем, не превосходящим 72, найдите ближайшую к числу 2+ Ö 5. Оцените погрешность.
3. Вычислите значение периодической цепной дроби a и напишите квадратное уравнение с целыми коэффициентами, корнем которого она является, если:
а)
б)
 .
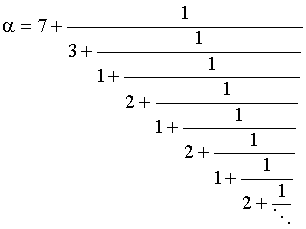4. Каждому, кто представит число 761 в виде суммы двух квадратов, специалисты по теории жмурок обещают в награду поллитровую бутылку Клейна и надкусанный марципан. Сделайте себе подарок. (Подсказка: 761 2 = 39 2 + 1).
|
|
|
|
|
|
|
