 |
Пункт 12. Целая и дробная часть.
|
|
|
|
Определение. Пусть x Î R - действительное число. Целой частью [ x ] числа x называется его нижнее целое, т.е. наибольшее целое, не превосходящее x; дробной частью { x } числа x называется число { x } = x - [ x ].
Примеры. [2,81] = 2; {2,81} = 0, 81; [- 0,2] = -1; {-0,2} = 0,8.
Отметим, что эти две функции известны каждому со школьной скамьи; что целая часть - неубывающая функция; что дробная часть - периодическая с периодом 1 функция; что дробная часть всегда неотрицательна, но меньше единицы; что обе эти функции разрывны при целых значениях x, но непрерывны при этих x справа; что лучшие мои годы уже прошли, а юношеские мечты так и не воплотились в реальность. Не осуждайте эти функции за их простоту, а лучше взгляните на их дальнейшие применения, порой изящные и неочевидные.
Лемма 1. Показатель, с которым простое число р входит в разложение n!, равен a = [ n / p ] + [ n / p 2 ] + [ n / p 3 ] +...
Доказательство. Очевидно, ряд [ n / p ] + [ n / p 2 ] + [ n / p 3 ] +... обрывается на том месте k, на котором p k превзойдет n. Имеем:
n! = 1· 2· 3·...· p·...· p 2 ...· p 3 ...· (n -1) · n.
Число сомножителей, кратных p, равно [ n / p ]. Среди них, кратных p 2 , содержится [ n / p 2 ]; кратных p 3 имеется [ n / p 3 ] и т.д. Сумма a и дает искомый результат, так как всякий сомножитель, кратный p m , но не кратный p m +1 , сосчитан в ней точно m раз: как кратный p, как кратный p 2 , как кратный p 3 ,..., как кратный p m .
¨
Пример. Показатель, с которым 5 входит в 643! равен:
[643/5] + [643/25] + [643/125] + [643/625] = 128 + 25 + 5 + 1 = 159.
Определение. Точка координатной плоскости называется целой, если обе ее координаты - целые числа.
Лемма 2. Пусть функция f (x) непрерывна и неотрицательна на отрезке [ a, b ]. Тогда число целых точек в области D = { a < x £ b, 0 < y £ f (x)} равно
.
Доказательство. На вертикальной прямой с целой абсциссой x в области D лежит [ f (x)] целых точек.
|
|
|
¨
Еще одно забавное утверждение про целые точки относится к области комбинаторной геометрии:
Лемма 3. Пусть М - многоугольник на координатной плоскости с вершинами в целых точках, контур М сам себя не пересекает и не касается, S - площадь этого многоугольника,
,
где суммирование ведется по всем целым точкам А, лежащим внутри и на границе этого многоугольника, причем d A = 1, если точка А лежит внутри М, и d A = 1/2, если точка А лежит на границе М. Тогда T = S.
Доказательство этой леммы я здесь приводить не буду так как эта лемма, вообще говоря, не относится к теории чисел. Намечу только схему этого доказательства.
1) Для треугольника с вершинами в целых точках и без целых точек внутри утверждение очевидно.
2) Для выпуклого многоугольника - фиксируем одну из его вершин и соединяем ее прямыми с остальными вершинами - попадаем в случай треугольников.
3) Случай невыпуклого многоугольника рассматриваем как разность выпуклых многоугольников.
¨
Что это я все время о целых частях, да о целых частях? Ассоциация независимых профсоюзов дробных частей уже собралась подавать на меня жалобу в ООН, поэтому я, чтобы не разжигать страсти, приведу замечательное утверждение о дробных частях, принадлежащее Лежену Дирихле (1805-1859).
Теорема. Для любого a Î R число 0 является предельной точкой последовательности x n = { a · n }.
Доказательство. Возьмем любое натуральное t и покажем, что неравенство
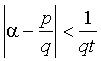
обязательно имеет решение в целых числах p и q, где q ³ 1. Пусть 0 = { a · 0}, { a · 1}, { a · 2},..., { a · (t -1)}, { a · t } - (t +1) штук чисел. Все они из отрезка [0, 1]. Разделим этот отрезок на t равных частей шагом 1/ t. По принципу Дирихле (именно для доказательства этой теоремы Дирихле и придумал свой знаменитый "принцип Дирихле" про t клеток и (t+ 1) кролика, которым негде сидеть) в одной из частей отрезка лежит два числа { a · k 1 } и { a · k 2 }, где k 2 > k 1 . Имеем:
|
|
|
| |{ a k 1 } - { a k 2 }| = | a (k 2 - k 1 ) - ([ a k 2 ] - [ a k 1 ])| < | t | . |
Положим k 2 - k 1 = q, [ a · k 2 ] - [ a · k 1 ] = p, ясно, что q £ t. Тогда будем иметь
| | a q - p | < | t | , 0 < q £ t. |
Это означает, что p / q - решение неравенства
.
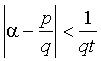Устремим t к бесконечности. Получим, что a q отлично от целого числа p менее, чем на 1/ t, а
.
Следовательно, либо 0, либо число 1 - предельная точка последовательности x n ={ a · n }. Если число 0 - предельная точка, то все доказано. Если же предельная точка - число 1, то тогда для любого e > 0, найдется член x последовательности x n такой, что x > 1 - e. Пусть x =1- d. Тогда 2 x = 2 - 2 d, а {2 x } (очевидно, что {2 x } - тоже член последовательности x n ) не дотягивает до 1 уже на 2 d; число {3 x } меньше 1 уже на 3 d, и т.д. Следовательно, можно подобрать такое натуральное k, что член { kx } будет меньше единицы на k d и попадет в e -окрестность нуля. Это означает, что число 0 также является предельной точкой последовательности x n , а именно это и требовалось.
¨
Очевидно, что если a = p / q - рациональное число, где (p, q) =1, то последовательность x n ={ a · n } является периодической с периодом q и ее членами являются только числа
| 0, | q | , | q | , …, | q -1 q | . |
Несколько модернизировав рассуждения из доказательства предыдущей теоремы, можно обосновать любопытное следствие, так же принадлежащее перу Дирихле.
Следствие. Если число a Î R иррационально, то члены последовательности x n ={ a · n } всюду плотно заполняют отрезок [0, 1].
Попытайтесь доказать это следствие самостоятельно, а я на этом пункт 12 заканчиваю.
Задачки 
| 1. Постройте графики функций:
а) y = [ x ];
б) y = { x };
в) y = [ x 2 ];
г) y = { x 2 }.
Особое внимание уделите плавности линий, проработке отдельных элементов композиции, грамотной прорисовке точек разрыва.
2. Аккуратно докажите следующие свойства целой части:
а) [ x + y ] ³ [ x ] + [ y ];
б) 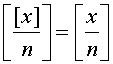 , где n Î N;
в)  ;
г)  , где n Î N.
3. Разложите на простые множители число 100! и подивитесь, у какого огромного числа вам удалось найти каноническое разложение!
4. Решите уравнение: x 3 - [ x ] = 3.
5. Докажите, что при любых a ¹ 0 и b, уравнение [ x ] + a { x } = b имеет [| a |] или [| a |]+1 решений.
6. Для каждого натурального n определите, сколько решений имеет уравнение x 2 - [ x 2 ] = { x } 2 на отрезке [1; n ].
7. Найдите предел:
 .
8. Докажите, что для любого натурального n имеет место оценка:
 ,
однако для любого e > 0, найдется натуральное n, удовлетворяющее неравенству
 .
9. Сколько целых точек лежит в области между осью абсцисс и параболой y = - x 2 + 30?
10. Найдите площадь многоугольника, который получится, если последовательно соединить отрезками точки А(0, 0), В(2, 7), С(4, 2), D(8, 8), E(10, 0), F(5, -5), A(0, 0).
11. Докажите, что для любого иррационального числа a Î Rнеравенство
имеет бесконечное множество решений (p, q) Î Z´ Nи, следовательно, знаменатели q всех решений неограничены. (1)
|
(1) В теории приближения действительных чисел рациональными числами утверждение этой задачи звучит так: Всякое иррациональное число допускает степенной порядок приближения 1/ q 2 . Это один из основополагающих фактов упомянутой теории.
|
|
|
|
|
|
