 |
Пункт 20. Сравнения любой степени по простому модулю.
|
|
|
|
В этом пункте мы рассмотрим сравнения вида f(x) º 0(mod p), где р - простое число, f(x)=ax n +a 1 x n-1 +…+a n - многочлен с целыми коэффициентами, и попытаемся научиться решать такие сравнения. Не отвлекаясь на посторонние природные явления, сразу приступим к работе.
Лемма 1. Произвольное сравнение f(x) º 0(mod p), где р - простое число, равносильно некоторому сравнению степени не выше p-1.
Доказательство. Разделим f(x) на многочлен x p -x (такой многочлен алгебраисты иногда называют "многочлен деления круга") с остатком: f(x)=(x p -x) × Q(x)+R(x), где, как известно, степень остатка R(x) не превосходит р-1. Но ведь, по теореме Ферма, x p -x º 0(mod p). Это означает, что f(x) º R(x)(mod p), а исходное сравнение равносильно сравнению R(x) º 0(mod p).
¨
Доказанная лемма приятна тем, что с ее помощью можно свести решение сравнения высокой степени к решению сравнения меньшей степени. Идем далее:
Лемма 2. Если сравнение ax n +a 1 x n-1 +…+a n º 0(mod p) степени n по простому модулю р имеет более n различных решений, то все коэффициенты a,a 1 ,…,a n кратны р.
Доказательство. Пусть сравнение ax n +a 1 x n-1 +…+a n º 0(mod p), имеет n+1 решение и x 1 ,x 2 ,…,x n ,x n+1 – наименьшие неотрицательные вычеты этих решений. Тогда, очевидно, многочлен f(x) представим в виде:
| f(x)=a(x-x 1 )(x-x 2 )…(x-x n -2)(x-x n-1 )(x-x n )+ +b(x-x 1 )(x-x 2 )…(x-x n -2)(x-x n-1 )+ +c(x-x 1 )(x-x 2 )…(x-x n -2)+ +…+ + k(x-x 1 )(x-x 2 )+ +l(x-x 1 )+ +m. |
Действительно, коэффициент b нужно взять равным коэффициенту при x n-1 в разности f(x)-a(x-x1)(x-x2)…(x-xn);
коэффициент с – это коэффициент перед x n-2 в разности f(x)-a(x-x 1 )(x-x 2 )…(x-x n )- b(x-x 1 )(x-x 2 )…(x-x n-1 ), и т.д.
Теперь положим последовательно x=x 1 ,x 2 ,…,x n ,x n+1 . Имеем:
1) f(x 1 )=m º 0(mod p), следовательно, р делит m.
2) f(x 2 )=m+l(x 2 -x 1 ) º l(x 2 -x 1 ) º 0(mod p), следовательно, р делит l, ибо р не может делить x 2 -x 1 , так как x 2 <p, x 1 <p.
3) f(x 3 ) º k(x 3 -x 1 )(x 3 -x 2 ) º 0(mod p), следовательно, р делит k.
И т.д.
|
|
|
Получается, что все коэффициенты a, b, c,...,k, l кратны р. Это означает, что все коэффициенты a,a 1 ,…,a n тоже кратны р, ведь они являются суммами чисел, кратных р. (Убедитесь в этом самостоятельно, раскрыв скобки в написанном выше разложении многочлена f(x) на суммы произведений линейных множителей.)
¨
Прошу обратить внимание на важность условия простоты модуля сравнения в формулировке леммы 2. Если модуль- число составное, то сравнение n -ой степени может иметь и более n решений, при этом, коэффициенты многочлена не обязаны быть кратными р. Пример: сравнение второй степени x 2 º 1(mod 16) имеет аж целых четыре различных решения (проверьте!):
x º 1(mod 16), x º 7(mod 16), x º 9(mod 16), x º 15(mod 16).
Подведем итог.
Всякое нетривиальное сравнение по mod p равносильно сравнению степени не выше p-1 и имеет не более p-1 решений.
Наступил момент, когда наших знаний стало достаточно, чтобы легко понять доказательство еще одной замечательной теоремы теории чисел – теоремы Вильсона. Александр Вильсон (1714–1786) – шотландский астроном и математик-любитель, трудился профессором астрономии в Глазго. Теоремы Ферма, Эйлера и Вильсона всегда идут сладкой троечкой во всех учебниках и теоретико-числовых курсах.
Теорема (Вильсон). Сравнение, (p-1)!+1 º 0(mod p) выполняется тогда и только тогда, когда р - простое число.
Доказательство. Пусть р - простое число. Если р=2, то, очевидно, 1!+1 º 0(mod 2). Если р>2, то рассмотрим сравнение:
[(x-1)(x-2)…(x-(p-1))]-(x p-1 -1) º 0(mod p).
Ясно, что это сравнение степени не выше р-2, но оно имеет р-1 решение: 1, 2, 3,..., р-1, т.к. при подстановке любого из этих чисел, слагаемое в квадратных скобках обращается в ноль, а (x p-1 ) сравнимо с нулем по теореме Ферма (х и р взаимно просты, т.к. х<р). Это означает, по лемме 2, что все коэффициенты выписанного сравнения кратны р, в частности, на р делится его свободный член, равный 1 × 2 × 3 ×... × (р–1)+1.
|
|
|
Так как коэффициенты многочлена являются значениями симметрических многочленов от его корней, то здесь наметился путь для доказательства огромного числа сравнений для симметрических многочленов. Однако, я по этому пути дальше не пойду, оставляя это прекрасное развлечение читателю, которому нечем коротать долгие зимние вечера.
Обратно. Если р – не простое, то найдется делитель d числа р, 1<d<p. Тогда (р–1)! делится на d, поэтому (р–1)!+1 не может делится на d и, значит, не может делиться также и на р. Следовательно, сравнение, (p-1)!+1 º 0(mod 2) не выполняется.
¨
Пример. 1 × 2 × 3 ×... × 10 + 1 = 3628800 +1 = 3628801 – делится на 11 (Вспомните признак делимости на 11- если сумма цифр в десятичной записи числа на четных позициях совпадает с суммой цифр на нечетных позициях, то число кратно 11).
Пример-задача. Доказать, что если простое число р представимо в виде 4n+1, то существует такое число х, что х 2 +1 делится на р.
Решение. Пусть р=4n+1 – простое число. По теореме Вильсона, (4n)!+1 делится на р. Заменим в выражении 1 × 2 × 3 ×... × (4n)+1 все множители большие (p-1)/2=2n через разности числа р и чисел меньших (p-1)/2=2n. Получим:
(p-1)!+1 = 1 × 2 × 3 × … × 2n × (p-2n)(p-2n+1) × … × (p-1) = (1 × 2 × 3 × … × 2n)[A × p+(-1) 2n × 2n × (2n-1) × … × 2 × 1]+1 = A 1 p+(1 × 2 × 3 × … × 2n) 2 )+1.
Так как это число делится на р, то и сумма (1 × 2 × 3 × … × 2n) 2 +1 делится на р, т.е. x=(2n)!=((p-1)/2)!.
¨
Мелким шрифтом добавлю, что только что рассмотренный пример-задача, тесно связан с проблематикой, касающейся представления натуральных чисел в виде сумм степеней (с показателями степени n>1) других натуральных чисел. Из нашего примера-задачи можно вывести, что натуральное число N в том и только в том случае представимо в виде суммы двух квадратов, когда в разложении N на простые множители все простые множители вида 4n+3 входят в четных степенях. Попробуйте самостоятельно доказать это утверждение в один из долгих зимних вечеров. Что касается представления чисел в виде сумм степеней, то здесь известна общая замечательная теорема:
Для любого натурального k существует такое натуральное N (разумеется, зависящее от k), что каждое натуральное число представимо в виде суммы не более чем N слагаемых, являющихся k-ми степенями целых чисел.
|
|
|
У этой теоремы было известно несколько различных неэлементарных доказательств, но в 1942 году ленинградский математик Ю. В. Линник придумал чисто арифметическое элементарное доказательство, которое, однако, является исключительно сложным (см., например, книжку А. Я. Хинчина "Три жемчужины теории чисел"). Что касается функции N(k), то здесь, в настоящее время почти ничего не ясно. Всякое натуральное число представимо в виде суммы четырех квадратов, девяти кубов (число 9 не может быть уменьшено), 21 штуки четвертых степеней (вот тут, кажется, что 21 может быть уменьшено до 19). Далее – полный туман. Всякое рациональное число представимо в виде суммы трех кубов рациональных чисел. (1) В качестве неплохого развлечения, предлагаю читателю следующую задачу: Доказать, что число 1 не может быть представлено в виде суммы двух кубов отличных от нуля рациональных чисел.
Задачки 
| 1.Какому сравнению степени ниже 7 равносильно сравнение: 2x 17 + 6x 16 + x 14 + 5x 12 + 3x 11 + 2x 10 + x 9 + 5x 8 + 2x 7 + 3x 5 + 4x 4 + 6x 3 + 4x 2 + x + 4 º 0(mod 7).
2. Используя процесс перебора всех вычетов из полной системы, решите сравнение 3x 14 + 4x 13 + 3x 12 + 2x 11 + x 9 + 2x 8 + 4x 7 + x 6 + 3x 4 + x 3 + 4x 2 + 2x º 0(mod 5) предварительно понизив его степень.
3.Пусть (a 0 , m)=1. Укажите сравнение n -ой степени со старшим коэффициентом 1, равносильное сравнению a 0 x n +a 1 x n-1 +...+a n º 0(mod m)
4.Докажите, что сравнение f(x) º 0(mod p), где р – простое, x n +a 1 x n-1 +...+a n-1 x+a n , n £ p имеет n решений тогда и только тогда, когда все коэффициенты остатка от деления x p -x на f(x) кратны р.
5.Перед вами крупная задачка, разделенная на несколько мелких частей. Решите их по порядку:
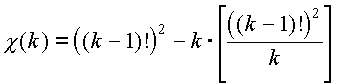 - характеристическая функция множества простых чисел. Докажите, что  где, как обычно, [x] - целая часть числа х.
б) Сообразите, что
 где p (m) – число простых чисел, не превосходящих m ("функция распределения" простых чисел).
в) Убедитесь, что
 где:  ("сигнум", т.е. знак х).
г) Пусть p n - n -ое в порядке возрастания простое число, т.е. p 1 =2, p 2 =3, p 3 =5,... Докажите, что p n £ n 2 +1 для всех n.
д) Докажите, что (Внимание! Перед вами формула, выражающая простое число p n через его номер!) (2): 
|
|
|
|
(1) Доказательство этого утверждения впервые получено в 1825 году. Выглядит оно потрясающе: для рационального числа а непосредственно пишется его представление в виде суммы трех кубов рациональных чисел:
Совершенно неясно, как додуматься до такого доказательства.
(2) Вопреки распространенному мнению о "невозможности задать простые числа формулой", довольно легко сконструировать выражение n-ого простого числа через его номер. Беда в том, что от подобных формул мало толку. Во-первых, вычисление по ним не короче вычисления при помощи решета Эратосфена, во-вторых, эти формулы отнюдь не облегчают исследование различных закономерностей, связанных с простыми числами (распределение простых чисел, наличие в множестве простых чисел арифметических прогрессий заданной длины и т.п.).
|
|
|
