 |
Пункт 22. Сравнения второй степени. Символ Лежандра.
|
|
|
|
В этом пункте мы будем подробно рассматривать простейшие двучленные сравнения второй степени вида
x 2 º a (mod p),
где а и р взаимно просты, а р - нечетное простое число. (Традиционная фраза “нечетное простое число”, на мой взгляд, несколько странновата. Глядя на нее, можно подумать, что четных простых чисел - пруд пруди, а она, всего-навсего, убирает из рассмотрения только число р =2.) Обратите внимание, что условие взаимной простоты (а, р)=1 исключает из нашего рассмотрения случай а =0.
Почему мы хотим исключить из дальнейших рассмотрений эти случаи? Нас будет интересовать вопрос, при каких а простейшее двучленное сравнение второй степени имеет решение, а при каких – не имеет. Ясно, что сравнение x 2 º a (mod 2) имеет решение при любых а, т.к. вместо а достаточно подставлять только 0 или 1, а числа 0 и 1 являются квадратами. Именно поэтому случай р =2 не представляет особого интереса и выводится из дальнейшего рассмотрения вышенаписанной странноватой фразой.
(Искушенный алгебраист объяснил бы эту ситуацию так: - всякий элемент любого поля характеристики 2 является квадратом, т.к. отображение x ® x 2 есть автоморфизм такого поля.)
Что касается сравнения x 2 º 0(mod p), то оно, очевидно, всегда имеет решение х =0. Итак, интерес представляет только ситуация с нечетным простым модулем и а ¹ 0, поэтому далее мы будем трудиться только в рамках оговоренных ограничений.
Определение. Если сравнение x 2 º a (mod p) имеет решения, то число а называется квадратичным вычетом по модулю р. В противном случае, число а называется квадратичным невычетом по модулю р.
Чтобы понять явление, надо сделать на него пародию. Всю стилистическую прелесть подобного определения (между прочим, общепринятого) и, в особенности, очарование содержащегося в нем термина “невычет” (в слитном написании), поможет прочувствовать аналогичная дефиниция: маленькое и жесткое хлебобулочное изделие тороидальной формы называется сушка. В противном случае, оно называется несушка. Впрочем, стилистических казусов в традиционной математической терминологии довольно много, например: нормальная подгруппа – ненормальная подгруппа, невязка – вязка и т.п.
|
|
|
Итак, если а – квадрат некоторого числа по модулю р, то а -“квадратичный вычет”, если же никакое число в квадрате не сравнимо с а по модулю р, то а - “квадратичный невычет”. Смиримся с этим.
Пример. Число 2 является квадратом по модулю 7, т.к.
4 2 º 16 º 2(mod7). Значит, 2 - квадратичный вычет. (Сравнение x 2 º 2(mod7) имеет еще и другое решение: 3 2 º 9 º 2(mod7).) Напротив, число 3 является квадратичным невычетом по модулю 7, т.к. сравнение x 2 º 3(mod7) решений не имеет, в чем нетрудно убедиться последовательным перебором полной системы вычетов: x = 0,1,2,3,4,5,6.
Простое наблюдение: Если а - квадратичный вычет по модулю р, то сравнение x 2 º a (mod p) имеет в точности два решения. Действительно, если а - квадратичный вычет по модулю р, то у сравнения x 2 º a (mod p) есть хотя бы одно решение x º x 1 (mod p). Тогда x 2 = - x 1 – тоже решение, ведь (- x 1 ) 2 =x 1 2 . Эти два решения не сравнимы по модулю р >2, так как из x 1 º - x 1 (mod p) следует 2 x 1 º 0(mod p), т.е. (поскольку р ¹ 2) x 1 º 0(mod p), что невозможно, ибо а ¹ 0.
Поскольку сравнение x 2 º a (mod p) есть сравнение второй степени по простому модулю, то больше двух решений оно иметь не может (см. пункт 20, лемма 2).
Еще одно простое наблюдение: Приведенная (т.е. без нуля) система вычетов
| – | p -1 | ,...,-2,-1,1,2,..., | p -1 |
по модулю р состоит из (p -1)/2 квадратичных вычетов, сравнимых с числами 1 2 ,2 2 ,…,((p -1)/2) 2 , и (p -1)/2 квадратичных невычетов, т.е. вычетов и невычетов поровну.
Действительно, квадратичные вычеты сравнимы с квадратами чисел
|
|
|
| – | p -1 | ,...,-2,-1,1,2,..., | p -1 |
т.е. с числами 1 2 ,2 2 ,…,((p -1)/2) 2 , при этом все эти квадраты различны по модулю р, ибо из k 2 º l 2 (mod p), где 0< k < l £ (p -1)/2, следует, что нетривиальное сравнение x 2 º k 2 (mod p) имеет аж четыре решения: l, –l, k, –k, что невозможно (см. пункт 20, лемма 2).
(Искушенный алгебраист опять-таки сказал бы больше: - квадраты (исключая 0) любого поля конечной характеристики, большей двух, образуют подгруппу индекса 2 мультипликативной группы этого поля. Эта подгруппа есть ядро эндоморфизма x ® x (p -1)/2 . Если есть желание, проверьте это утверждение самостоятельно.)
Согласитесь, что фраза “ Число а является квадратичным вычетом (или невычетом) по модулю р “ несколько длинновата, особенно если ее приходится часто употреблять при доказательстве какого-либо утверждения. В свое время божественная длиннота этой фразы тревожила и знаменитого французского математика Адриена-Мари Лежандра (того самого, который имеет прямое отношение к ортогональным полиномам и многим другим математическим открытиям, но, по-видимому, не имеет никакого отношения к развитию футбола в странах Карибского бассейна). Он предложил изящный выход, введя в рассмотрение удобный символ (a / p), заменяющий длинную фразу. Этот символ носит теперь фамилию Лежандра и читается: “символ Лежандра а по пэ”.
Определение. Пусть а не кратно р. Тогда символ Лежандра определяется как:
| если а - квадратичный вычет по модулю р. если а - квадратичный невычет по модулю р. |
Оказывается, что символ Лежандра есть не просто удобное обозначение. Он имеет много полезных свойств и глубокий смысл, уходящий корнями в теорию конечных полей. Далее в этом пункте мы рассмотрим некоторые простейшие свойства символа Лежандра и, прежде всего, научимся его вычислять (т.е., тем самым, научимся отвечать на вопрос, проставленный в начале пункта: при каких а простейшее двучленное сравнение второй степени имеет решение, а при каких – не имеет?).
Теорема. (Критерий Эйлера) Пусть а не кратно р. Тогда:
a (p -1)/2 º (a / p)(mod p).
Доказательство. По теореме Ферма, a p -1 º 1(mod p) т.е.
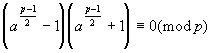. В левой части последнего сравнения в точности один сомножитель делится на р, ведь оба сомножителя на р делиться не могут, иначе их разность, равная двум, делилась бы на р >2. Следовательно, имеет место одно и только одно из сравнений:
|
|
|
a (p -1)/2 º 1(mod p)
a (p -1)/2 º -1(mod p)
Но всякий квадратичный вычет а удовлетворяет при некотором х сравнению a º x 2 (mod p) и, следовательно, удовлетворяет также получаемому из него почленным возведением в степень (p -1)/2 сравнению
a (p -1)/2 º x p-1 º 1(mod p) (опять теорема Ферма). При этом, квадратичными вычетами и исчерпываются все решения сравнения
a (p -1)/2 º 1(mod p), т.к., будучи сравнением степени (p -1)/2, оно не может иметь более (p -1)/2 решений. Это означает, что квадратичные невычеты удовлетворяют сравнению a (p -1)/2 º -1(mod p)
¨
(Свойство a (p -1)/2 º (a / p)(mod p), даваемое критерием Эйлера, можно было бы сразу принять за определение символа Лежандра, показав, конечно, предварительно, с помощью теоремы Ферма, что a (p -1)/2 º ± 1(mod p) Именно так частенько и поступают в книжках по теории конечных полей.)
Пример. Крошка-сын к отцу пришел, и спросила кроха: “Будет ли число 5 квадратом по модулю 7?”. Гигант-отец тут же сообразил:
5 (7-1)/2 =5 3 =125=18 × 7-1 º -1(mod7),
т.е. сравнение x 2 º 5(mod7) решений не имеет и 5 - квадратичный невычет по модулю 7. Кроха-сын, расстроенный, пошел на улицу делиться с друзьями полученной информацией.
Перечислим далее, кое-где доказывая или комментируя, простейшие свойства символа Лежандра.
Свойство 1. Если a º b (mod p), то (a / p)=(b / p).
Это свойство следует из того, что числа одного и того же класса по модулю р будут все одновременно квадратичными вычетами либо квадратичными невычетами.
Свойство 2. (1/ p)=1.
Доказательство очевидно, ведь единица является квадратом.
Свойство 3.
.
Доказательство этого свойства следует из критерия Эйлера при а =-1. Так как (p -1)/2 – четное, если р вида 4 n +1, и нечетное, если р вида 4 n +3, то число -1 является квадратичным вычетом по модулю р тогда и только тогда, когда р вида 4 n +1.
Свойство 4.
.
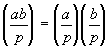Действительно,
. Cвойство 4, очевидно, распространяется на любое конечное число сомножителей в числителе символа Лежандра, взаимно простых с р. Кроме того, из него следует
|
|
|
Свойство 5. 
, т.е. в числителе символа Лежандра можно отбросить любой квадратный множитель. Действительно:
Запомним хорошенько эти пять перечисленных простейших свойств символа Лежандра и устремимся дальше, в пункт 23, где нам раскроются свойства более сложные и глубокие, поразительные и загадочные. Вперед!
Задачки 
| 1.Среди вычетов приведенной системы по модулю 37 укажите квадратичные вычеты и квадратичные невычеты.
2.Посчитайте символ Лежандра, умело пользуясь его свойствами: а) (20/7); б) (200/43); в) (1601600/839).
3.С помощью критерия Эйлера установите, имеет ли решение сравнение x 2 º 5(mod13)?
4.С помощью символа Лежандра установите, имеют ли решения сравнения: а) x 2 º 22(mod13);
б) x 2 º 239(mod661);
в) x 2 º 412(mod421)?
5.Решите сравнения:
а) x 2 º 7(mod137);
б) x 2 º 23(mod101).
6.Докажите, что:
а) сравнение x 2 +1 º 0(mod p) разрешимо тогда и только тогда, когда р - простое число вида 4 m +1;
б) сравнение x 2 +2 º 0(mod p) разрешимо тогда и только тогда, когда р - простое число вида 8 m +1 или вида 8 m +3;
в) сравнение x 2 +3 º 0(mod p) разрешимо тогда и только тогда, когда р - простое число вида 6 m +1.
7.Умело используя теорему Вильсона, докажите, что решениями сравнения x 2 +1 º 0(mod p), где р - простое число вида 4 m +1, являются числа x 1,2 º ± (2 m)!(mod p) и только они.
8.Докажите, что сравнение x 2 º a (mod p a ), где a >1, р >2, имеет два решения или же ни одного, в зависимости от того, будет ли число а квадратичным вычетом или же невычетом по модулю р.
9.Исследуйте самостоятельно сравнение вида x 2 º a (mod2 a ), a >1. При каких условиях на числа а и a это сравнение имеет решения и сколько оно их имеет? Найдите эти решения.
10.Докажите, что решениями сравнения x 2 º a (mod p a ), где (a, p)=1, р >2, будут числа x º ± PQN (mod p a ), где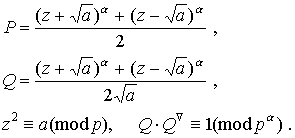 
11.Докажите, что число различных разложений натурального числа n на сумму квадратов двух целых чисел равно учетверенному избытку числа делителей n вида 4 k +1 над числом делителей вида 4 k +3. * )
|
|
|
|
