 |
Историческое отступление про Гаусса.
|
|
|
|
Карл Фридрих Гаусс (1777 – 1855) – величественная фигура математики рубежа восемнадцатого - девятнадцатого столетий. Он родился в немецком городке Брауншвейге, был сыном поденщика. Математические способности Гаусса проявились очень рано, а, согласно его дневникам, в 17 лет Карл Фридрих уже начал делать выдающиеся математические открытия. Дебютом Гаусса явилось доказательство возможности построения правильного семнадцатиугольника циркулем и линейкой (Записью об этом открывается дневник Гаусса – удивительная летопись гениальных открытий. Запись датирована 30 марта 1796 года). Отдадим должное герцогу Брауншвейгскому, который обратил внимание на вундеркинда Гаусса и позаботился о его обучении. В 1795 – 1798 годах юный гений учился в Геттингенском университете, в 1799 году он получил степень доктора, а с 1807 года до самой смерти он спокойно работал в качестве директора астрономической обсерватории и профессора математики Геттингенского университета. Как и его великие современники Кант, Гете, Бетховен и Гегель, Гаусс не вмешивался в яростные политические события той эпохи (“Буря и натиск”, наполеоновские войны, Великая Французская революция и т.п.), но в области математики он очень ярко выразил новые идеи своего века.
Обладая феноменальными вычислительными способностями, Гаусс составил огромные таблицы простых чисел (ему были известны все простые числа, меньшие пяти миллионов) и самостоятельно, путем внимательного их разглядывания, он открыл квадратичный закон взаимности (до Гаусса этот закон впервые подметил Эйлер, но не смог его доказать): если р и q – два нечетных простых числа, то
Сам Гаусс не пользовался для записи этого закона символом Лежандра, хотя знал этот формализм (Лежандр был на 20 лет старше Гаусса), да и выражения “квадратичная взаимность” у Гаусса нет (его потом придумал Дирихле). В знаменитой книге Гаусса “Арифметические исследования”, которая считается родоначальницей современной теории чисел (издана в Лейпциге, в 1801 году), отмечается, что сам закон квадратичной взаимности впервые сформулировал Эйлер, подробно обсуждал Лежандр, но до 1801 года не было опубликовано ни одного строгого доказательства этого закона. Свое первое доказательство закона взаимности Гаусс (а он, впоследствии, придумал их аж шесть штук!) получил в 1796 году * ), в девятнадцатилетнем возрасте, ценой невероятного напряжения. На отыскание первого доказательства у Гаусса ушло более года работы, которая, по меткому выражению Кроннекера, явилась серьезной “пробой гауссовского гения”. Столь выдающийся результат Гаусса был назван современниками (конечно, не всеми, а только смыслящими в математике) “золотая теорема” (“theorema aurum”). Давайте и мы познакомимся с этой золотой теоремой.
|
|
|
Нам понадобится несколько дополнительных свойств символа Лежандра (a / p), которые я сформулирую в виде лемм.
Пусть р – нечетное простое число, S ={1,2,…,(p -1)/2} - множество всех положительных чисел из приведенной системы вычетов по модулю р.
Рассмотрим сравнение a × s º e s r s (mod p), где а - числитель исследуемого символа Лежандра, s Î S, e s r s - абсолютно наименьший вычет числа as по модулю р (т.е. вычет, абсолютная величина которого наименьшая), r s - абсолютная величина этого вычета, а e s , стало быть, его знак. Таким образом, r s Î S, а e s = ± 1.
Лемма 1 (Гаусс).
.
Доказательство. Рассмотрим сравнения
(*)
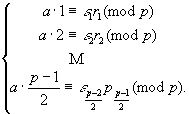Множество чисел
является приведенной системой вычетов по модулю р (Если забыл, см. пункт 17, лемма 2, если забыла, см. там же.). Их абсолютно наименьшие вычеты соответственно суть
,
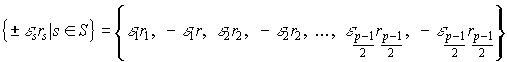положительные же из них, т.е. r 1 , r 2 ,…, r (p -1)/2 , совпадают с числами 1,2,…,(p -1)/2, т.е. образуют множество S. Перемножим теперь почленно сравнения (*) и сократим произведение на
|
|
|
.
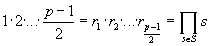Получим:
a (p -1)/2 º e 1 e 2 … e (p -1)/2 (mod p)
Согласно критерию Эйлера из предыдущего пункта, a (p -1)/2 º (a/p)(mod p) т.е.
, что и требовалось.
¨
Лемма 2. При нечетном а,
, где [ as/p ] - целая часть числа as/p.
Доказательство. Имеем:
,
что будет четным или нечетным, в зависимости от того, будет ли наименьший неотрицательный вычет числа as меньше или больше числа p /2, т.е. будет ли e s =1 или e s =-1. Отсюда, очевидно,
,
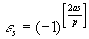поэтому, в силу леммы Гаусса,
.
Преобразуем это равенство (помним, что а + р – четное, а квадратичный множитель из числителя символа Лежандра можно отбрасывать):
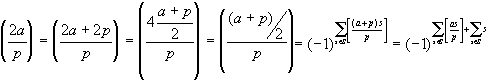
Поскольку(2 a / p)=(2/ p)(a / p), а
, то лемма 2 доказана.
¨
Лемма 3.
.
Доказательство. Непосредственно следует из леммы 2 при а =1.
¨
Ни у кого не должно возникать недоумения по поводу возможности деления числа p 2 -1=(p -1)(p +1) на 8 нацело, т.к. из двух последовательных четных чисел одно обязательно делится на 4. Кроме того, простое число р можно представить в виде p= 8 n + k, где k – одно из чисел 1, 3, 5, 7. Так как число
| (8 n + k) 2 -1 | k 2 -1 | |
| =8 n +2 +2 nk + | ||
будет четным при k =1 и k =7, то 2 будет квадратичным вычетом по модулю р, если р вида 8 n +1 или 8 n +7. Если же р вида 8 n +3 или 8 n +5, то 2 будет квадратичным невычетом.
Теорема (Закон взаимности квадратичных вычетов). Если p и q - нечетные простые числа, то
.
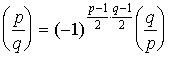Другими словами, если хоть одно из чисел p или q вида 4 n +1, то р квадрат по модулю q тогда и только тогда, когда q квадрат по модулю р. Если же оба числа p и q вида 4 n +3, то р квадрат по модулю q тогда и только тогда, когда q не является квадратом по модулю р.
Доказательство. Поскольку
, то формула из леммы 2 принимает вид:
.
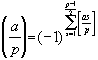Рассмотрим два множества:
S ={1,2,…, (p -1)/2} и K ={1,2,…,(q -1)/2}.
Образуем (p -1)/2 × (q -1)/2 штук пар чисел (qx,py), где х пробегает S, a y пробегает К. Первая и вторая компонента одной пары никогда не совпадают, ибо из py = qx следует, что py кратно q. Но ведь это невозможно, так как (p,q)=1 и, поскольку 0< y < q, то (y, q)=1.
Положим, поэтому, (p -1)/2 × (q -1)/2= V 1 + V 2 , где V 1 – число пар, в которых первая компонента меньше второй (qx < py), V 2 – число пар, в которых вторая компонента меньше первой (qx > py).
|
|
|
Очевидно, что V 1 есть число пар, в которых x < (p / q) y. (Вообще-то, x £ (p -1)/2, но (p / q) y < p /2 т.к. y/q < 1/2, следовательно [(p / q) y ] £ [ p/ 2]= (p -1)/2, и неравенство x <(p / q) y не противоречит неравенству x £ (p -1)/2.) Поэтому,
.
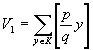Аналогично,
.
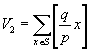Тогда равенство из леммы 2, отмеченное в начале этого доказательства, дает:
.
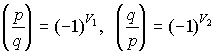Это означает, что
, а это, собственно, и требовалось.
¨
Барабанная дробь и фанфары!
Справедливости ради, следует отметить мелким шрифтом, что мы могли бы доказать закон взаимности в этом пункте сразу после леммы 1, но при этом упустили бы из виду важные свойства символа Лежандра, которые спрашивают на кандидатском экзамене по специальности “Алгебра, математическая логика и теория чисел”. Кроме того, “быстрое” доказательство закона взаимности страдает существенным недостатком – совершенно непонятно, как до него додуматься. А додумался до него немецкий математик Фердинанд Готхольд Эйзенштейн (1823–1852). Это доказательство, дословно почерпнутое из замечательной книжки Ж.П.Серра “Курс арифметики”, перед вами.
Тригонометрическая лемма. Пусть m – нечетное натуральное число. Тогда
.
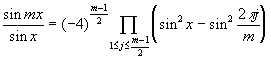Доказательство получается непосредственной проверкой. Например, по формуле Муавра, убеждаемся, что левая часть есть полином степени (m -1)/2 от sin 2 x, корни которого есть sin 2 (2 p j/m), где 1 £ j £ (m -1)/2. Множитель (-4) (m -1)/2 получается сравнением коэффициентов в левой и правой частях.
Доказательство закона взаимности. Пусть р и q – два различных нечетных простых числа. По лемме Гаусса,
. В силу равенства qs = e s r s (обозначения леммы 1 сохранены), имеем:
.
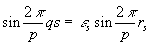(Синус-то функция нечетная, и знак можно вынести вперед.)
Перемножая эти равенства и учитывая, что отображение s ® r s биективно, получаем
.
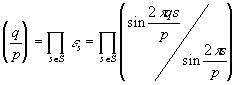Применим теперь тригонометрическую лемму при m = q:
.
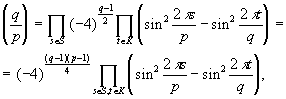где K ={1,2,…(q -1)/2}. Меняя роли q и р, точно так же получим:
Множители в формулах для (q/p) и (p/q) одинаковы с точностью до знака. Число же противоположных знаков равно
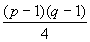, поэтому
.
¨
На этом пункт 23 и с ним весь параграф, посвященный теории сравнений закончим. С удовлетворением отмечу, что если мы и не все познали в сравнении, то весьма немало. Примите мои сердечные поздравления.
|
|
|
Задачки 
| 1.Используя закон взаимности для “переворачивания” символа Лежандра, посчитайте: а) (59/269); б) (37/557); в) (43/991). 2.Докажите, что число а одновременно является или квадратичным вычетом или квадратичным невычетом для всех простых чисел, входящих в арифметическую прогрессию 4 at + r, t =0,1,2…, где r - произвольное натуральное число, меньшее 4 а.) ** 3.Пусть p и q - простые числа и p + q =4 а. Докажите, что тогда число а является одновременно или квадратичным вычетом по модулям p и q или квадратичным невычетом. |
Трансцендентные числа.
В этом параграфе мы снова покинем прекрасное и уютное царство целых чисел, по которому разгуливали (чуть было не сказал - слонялись) изучая теорию сравнений. Если проследить историю возникновения и развития знаний человечества о числах, то выявится довольно парадоксальный факт - на протяжении почти всей своей многовековой истории человечество использовало на практике и пристально изучало исключительно малую долю всего множества живущих в природе чисел. Люди долгое время совершенно не подозревали о существовании, как выяснилось впоследствии, подавляющего большинства действительных чисел, наделенных удивительными и загадочными свойствами и называемых теперь трансцендентными. Судите сами (перечисляю ориентировочные этапы развития понятия действительного числа):
1) Идущая из глубины тысячелетий гениальная математическая абстракция натурального числа
Гениальность этой абстракции поражает, а ее значение для развития человечества превосходит, наверное, даже изобретение колеса. Мы привыкли к ней настолько, что перестали восхищаться этим самым выдающимся достижением человеческого разума. Однако попробуйте, для пущей достоверности представив себя не студентом-математиком, а первобытным человеком, или, скажем, студентом-филологом, сформулировать точно, что общего имеется между тремя хижинами, тремя быками, тремя бананами и тремя ультразвуковыми томографами (что общего между тремя собутыльниками мы здесь не рассматриваем). Объяснять не математику, что такое натуральное число “три” - почти безнадежная затея, однако уже пятилетний человеческий детеныш внутренне ощущает эту абстракцию и в состоянии разумно оперировать с ней, выпрашивая у мамы три конфеты вместо двух.
2) Дроби, т.е. положительные рациональные числа
Дроби естественно возникли при решении задач о разделе имущества, измерении земельных участков, исчислении времени и т.п. В древней Греции рациональные числа вообще являлись символом гармонии окружающего мира и проявлением божественного начала, а все отрезки, до некоторого времени, считались соизмеримыми, т.е. отношение их длин обязано было выражаться рациональным числом, иначе - труба (а боги этого допустить не могут).
|
|
|
3) Отрицательные числа и ноль (согласно некоторым научным источникам
Отрицательные числа первоначально трактовались как долг при финансовых и бартерных расчетах, однако потом выяснилось, что без отрицательных чисел и в других областях человеческой деятельности никуда не денешься (кто не верит, пусть посмотрит зимой на градусник за окном). Число ноль, на мой взгляд, первоначально служило скорее не символом пустого места и отсутствием всякого количества, а символом равенства и завершенности процесса расчетов (сколько был должен соседу, столько ему и отдал, и вот теперь – ноль, т.е. жалко).
4) Иррациональные алгебраические числа
Иррациональные числа открыли в пифагорейской школе при попытке соизмерить диагональ квадрата с его стороной, но хранили это открытие в страшной тайне – как бы смуты не вышло! В это открытие посвящались только наиболее психически устойчивые и проверенные ученики, а истолковывалось оно как отвратительное явление, нарушающее гармонию мира. Но нужда и война заставили человечество учиться решать алгебраические уравнения не только первой степени с целыми коэффициентами. После Галилея снаряды стали летать по параболам, после Кеплера планеты полетели по эллипсам, механика и баллистика стали точными науками и везде нужно было решать и решать уравнения, корнями которых являлись иррациональные числа. Поэтому с существованием иррациональных корней алгебраических уравнений пришлось смириться, какими бы отвратительными они не казались. Более того, методы решения кубических уравнений и уравнений четвертой степени, открытые в 16 веке итальянскими математиками Сципионом дель Ферро, Никколо Тартальей (Тарталья – это прозвище, означающее в переводе – заика, настоящей его фамилии я не знаю), Людовиком Феррари и Рафаэлем Бомбелли привели к изобретению совсем уж “сверхъестественных” комплексных чисел, которым суждено было получить полное признание только в 19 веке. Алгебраические иррациональности прочно вошли в человеческую практику уже с 16 века.
В этой истории развития понятия числа не нашлось места для трансцендентных чисел, т.е. чисел не являющихся корнями никакого алгебраического уравнения с рациональными или, что равносильно (после приведения к общему знаменателю), целыми коэффициентами. Правда, еще древние греки знали замечательное число p, которое, как выяснилось впоследствии, трансцендентно, но они знали его только как отношение длины окружности к ее диаметру. Вопрос об истинной природе этого числа вообще мало кого интересовал до тех пор, пока люди вдоволь и безуспешно не нарешались древнегреческой задачей о квадратуре круга, а само число p каким-то загадочным образом повылезало в разных разделах математики и естествознания.
Лишь только в 1844 году Лиувилль построил исторически первый пример трансцендентного числа, а математический мир удивился самому факту существования таких чисел. Лишь только в 19 веке гениальный Георг Кантор понял, используя понятие мощности множества, что на числовой прямой трансцендентных чисел подавляющее большинство. Лишь только в пятом параграфе этой небольшой книжки мы, наконец-то, обратим на трансцендентные числа свое внимание.
|
|
|
