 |
Пункт 21. Сравнения любой степени по составному модулю.
|
|
|
|
Переход от решения сравнений по простому модулю к a priori более сложной задаче — решению сравнений по составному модулю (переход от пункта 20 к пункту 21) осуществляется быстро и без лишних затей с помощью следующей теоремы:
Теорема 1. Если числа m 1 , m 2 ,… m k попарно взаимно просты, то сравнение f (x) º 0(mod m 1 m 2 … m k ) равносильно системе сравнений:
При этом, если Т 1 , Т 2 ,..., Т к — числа решений отдельных сравнений этой системы по соответствующим модулям, то число решений Т исходного сравнения равно Т 1 Т 2 ...Т к .
Доказательство. Первое утверждение теоремы (о равносильности системы и сравнения) очевидно, т.к. если a º b (mod m), то a º b (mod d), где d делит m. Если же a º b (mod m 1 ) и a º b (mod m 2 ), то a º b (mod HOK (m 1 , m 2 )), где НОК (m 1 , m 2 )– наименьшее общее кратное m 1 и m 2 . (Вспомните простейшие свойства сравнений из пункта 16).
Обратимся ко второму утверждению теоремы (о числе решений сравнения).
Каждое сравнение f (x) º 0(mod m s ) выполняется тогда и только тогда, когда выполняется одно из T s штук сравнений вида x º b s (mod m s ), где b s пробегает вычеты решений сравнения f (x) º 0(mod m s ). Всего различных комбинаций таких простейших сравнений
Т 1 Т 2 ...Т к штук. Все эти комбинации, по лемме 2 из пункта 19, приводят к различным классам вычетов по mod(m 1 m 2 … m k ).
¨
Итак, решение сравнения 
сводится к решению сравнений вида f (x) º 0(mod p a ). Оказывается, что решение этого последнего сравнения, в свою очередь, сводится к решению некоторого сравнения g (x) º 0(mod p) c другим многочленом в левой части, но уже с простым модулем, а это, просто напросто, приводит нас в рамки предыдущего пункта. Сейчас я расскажу процесс сведения решения сравнения f (x) º 0(mod p a ) к решению сравнения g (x) º 0(mod p).
|
|
|
Процесс сведения.
Очевидно, выполнение сравнения f (x) º 0(mod p a ) влечет, что х подходит в сравнение f (x) º 0(mod p). Пусть x º x 1 (mod p) – какое-нибудь решение сравнения f (x) º 0(mod p). Это означает, что
x = x 1 + p × t 1 , где t 1 Î Z.
Вставим это х в сравнение f (x) º 0(mod p 2 ). Получим сравнение
f (x 1 + p × t 1 ) º 0(mod p 2 ),
которое тоже, очевидно, выполняется.
Разложим далее (не пугайтесь!) левую часть полученного сравнения по формуле Тейлора по степеням (х - х 1 ):
Но, ведь, x = x 1 + p × t 1 , следовательно,
.
Заметим, что число f (k) (x 1 )/ k! всегда целое, т.к. f (x 1 + p × t 1 ) — многочлен с целыми коэффициентами. Теперь в сравнении
f (x 1 + p × t 1 ) º 0(mod p 2 )
можно слева отбросить члены, кратные р 2 :
.
Разделим последнее сравнение и его модуль на р:
.
Заметим, опять, что f (x 1 )/ p — целое число, т.к. f (x 1 ) º 0(mod p). Далее ограничимся случаем, когда значение производной f ¢ (x 1 ) не делится на р. В этом случае имеется всего одно решение сравнения первой степени
относительно t 1 :
t 1 º t 1 Ñ (mod p).
Это, опять-таки, означает, что t 1 = t 1 Ñ + p × t 2 , где t 2 Î Z, и
.
Снова вставим это x = x 2 + p 2 t 2 в сравнение f (x) º 0(mod p 3 ) (но теперь это сравнение уже по mod p 3 , разложим его левую часть по формуле Тейлора по степеням (х-х 2 ) и отбросим члены, кратные p 3 :
f (x 2 ) +(f ¢ (x 2 )/1!) × p 2 t 2 º 0(mod p 3 ).
Делим это сравнение и его модуль на р 2 :
f (x 2 )/ p 2 + f ¢ (x 2 ) × t 2 º 0(mod p).
Опять-таки f (x 2 )/ p 2 — целое число, ведь число t 1 Ñ такое, что f (x 1 + p × t 1 Ñ ) º 0(mod p 2 ). Кроме того, x 2 º x 1 (mod p), значит f ¢ (x 2 ) º f ¢ (x 1 )(mod p), т.е. f ¢ (x 2 ), как и f ¢ (x 1 ), не делится на р. Имеем единственное решение сравнения первой степени f (x 2 )/ p 2 + f ¢ (x 2 ) × t 2 ) º 0(mod p) относительно t 2 :
t 2 º t 2 Ñ (mod p).
Это, опять-таки, означает, что t 2 = t 2 Ñ + p × t 3 , где t 3 Î Z, и
и процесс продолжается дальше и дальше, аналогично предыдущим шагам, до достижения степени p a , в которой стоит простое число р в модуле исходного сравнения f (x) º 0(mod p a ).
|
|
|
Итак:
Всякое решение x º x 1 (mod p) сравнения f (x) º 0(mod p), при условии p/ f ¢ ¢ (x 1 ), дает одно решение сравнения f (x) º 0(mod p a ) вида x º x a + p a t a , т.е. x º x a (mod p a ).
¨
Пример. Решить сравнение x 4 +7 x +4 º 0(mod27).
Решение. Весь богатейший педагогический опыт, накопленный человечеством к моменту написания этой книжки, показывает, что наиболее одаренные ученики в состоянии догадаться без посторонней помощи, что 27=3 3 . Далее, получив небольшую подсказку в форме бодрящей мимики и вскриков преподавателя, ученики обычно оказываются в состоянии проверить перебором полной системы вычетов по mod3, что сравнение x 4 +7 x +4 º 0(mod3) имеет всего одно решение x º 1(mod3). По поводу дальнейших возможностей учеников ничего определенного спрогнозировать нельзя, но последующий процесс решения, в идеале, должен быть таким:
f ¢ (x)=(4 x 3 +7) ½ x º 1 º 2(mod3),
т.е. не делится на р = 3. Далее:
x 1 =1+3 × t 1
f (1)+ f ¢ (1) 3 × t 1 º 0(mod3 2 )
Ищем t 1 :
3+3 t 1 × 2 º 0(mod9),
после деления на р =3:
1+2 t 1 º 0(mod3),
t 1 º 1(mod3)
- единственное решение. Далее:
t 1 =1+3 t 2 ,
x =1+3 t 1 =4+9 t 2 ,
f (4)+9 × t 2 × f ¢ (4) º 0(mod p 3 =27),
18+9 × 20 × t 2 º 0(mod27),
и, после деления на p 2 =9, ищем t 2 :
2+20 t 2 º 0(mod3),
t 2 º 2(mod3),
t 2 =2+3 t 3 ,
откуда
x =4+9 × (2+3 t 3 )=22+27 t 3 .
Значит, единственным решением исходного сравнения является x º 22(mod27).
¨
Следующая теорема относится к специфическому, но весьма приятному виду сравнений.
Теорема 2. Пусть A, m, n - натуральные числа; (A, m)=1,
x º x 0 (mod m) — одно из решений сравнения
x n º A (mod m).
Тогда все решения этого сравнения получаются умножением x 0 на вычеты решений сравнения y n º 1(mod m).
Доказательство. Перемножим сравнения:
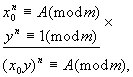
откуда видно, что x 0 y — решения сравнения x n º A (mod m).
Если теперь 
, то 
. Действительно, предположим, что x 0 y 1 º x 0 y 2 (mod m). Очевидно, что (x 0 , m)=1, т.к. иначе было бы:
x 0 = d × x 0 Ñ , m = d × m Ñ ,
x 0 = d n (x 0 Ñ ) n º A (mod d m Ñ ),
cледовательно d делит А и делит m, что противоречит взаимной простоте А и m. Значит (x 0 , m)=1 и сравнение x 0 y 1 º x 0 y 2 (mod m)
можно поделить на x 0 : y 1 º y 2 (mod m) — а это противоречит исходному предположению. Таким образом, для разных y 1 и y 2 , получаются разные решения.
Осталось убедиться, что каждое решение сравнения x n º A (mod m) получается именно таким способом. Имеем:
|
|
|
x n º A (mod m)
x 0 n º A (mod m),
следовательно, x n º x 0 n (mod m). Возьмем число y такое, что x º y × x 0 (mod m). Тогда y n x 0 n º x 0 n (mod m), т.е. y n º 1(mod m).
¨
Пункт с номером 21 (очко!) закончен.
Задачки 
| 1.Сколько решений имеет сравнение x 5 + x +1 º 0(mod105)? 2.Решите сравнения: а) 7 x 4 +19 x +25 º 0(mod27); б) 9 x 2 +29 x +62 º 0(mod64); в) 6 x 3 +27 x 2 +17 x +20 º 0(mod30); г) 31 x 4 +57 x 3 +96 x +191 º 0(mod225); д) x 3 +2 x +2 º 0(mod125); е) x 4 +4 x 3 +2 x 2 +2 x +12 º 0(mod625). |
|
|
|
