Варьируемых факторов и интервала их варьирования

В литературе по планированию эксперимента для отыскания поверхности отклика рекомендуется ставить эксперименты типа 2^k, а поверхность отклика задавать уравнением первой или второй степени. Затем на основании результатов эксперимента определяется справедливость описания действительности с заданными уравнениями. Однако такой путь слишком трудоемок и неэффективен. Действительно, если окажется, что уравнения плохо согласуются, то эксперимент надо повторять с новым набором исходных данных до тех пор, пока не будет получено хорошее согласие. Но даже в случае быстрого получения хорошего согласия уравнений с результатами наблюдений может оказаться, что они справедливы только для локальной поверхности исследования, и при небольшом удалении от нее поверхность отклика будет описываться другим уравнением, следовательно, надо снова ставить эксперименты для нахождения этого уравнения. Поэтому целесообразнее уже на первой стадии эксперимента оценить, какой эффект — линейный, квадратичный или кубический — оказывает каждый фак-тор и их взаимодействие на протекание процессов в объекте. Зная это, можно с большей определенностью решать вопрос о характере уравнения поверхности отклика. Для этого необходимо опреде­лить минимальное количество уровней факторов, испытания на которых позволят оценить указанные эффекты. Для определения линейного и квадратичного эффектов надо иметь не менее трех уровней факторов X_t. Если фактор меняется на четырех уровнях, то можно выделить линейный, квадратичный и кубический эф­фекты, подбирая особым образом коэффициенты для суммарных откликов. Для ускорения решения этой задачи имеются таблицы ортогональных полиномов, которые дают соответствующие коэф­фициенты в зависимости от количества уровней фактора.

О существовании взаимодействия между факторами говорят тогда, когда изменение одного фактора сопровождается различны­ми изменениями результатов эксперимента при разных уровнях другого фактора. В принципе, для определения взаимодействия между факторами достаточно провести факторный эксперимент типа 2^k, однако установить по результатам такого эксперимента сте­пень взаимодействия между факторами не представляется возмож­ным. Поэтому необходимо иметь для каждого фактора более двух уровней. Тогда появляется возможность оценить степень взаимо­действия кубического эффекта одного фактора с кубическим эф­фектом всех остальных факторов.

Однако на практике часто бывает трудно дать интерпретацию некоторым из высоких полиномиальных взаимодействий, поэто­му ограничиваются определением только взаимодействий линей­ных эффектов, линейных с квадратичными и квадратичных с ли­нейными, а оставшиеся рассматриваются вместе как остаточное взаимодействие. Для определения указанных степеней взаимодей­ствий достаточно иметь в матрице планирования четыре уровня каждого фактора. Дальнейшее увеличение количества уровней ведет к неоправданному усложнению эксперимента, увеличивает его продолжительность и усложняет вычислительные работы. Поэтому будем считать, что для проведения испытаний объектов на воздействие факторов внешней среды для каждого фактора дос­таточно четырех уровней.

Назначая для каждого фактора четыре уровня, необходимо определить интервалы между ними. Выбор интервала варьирова­ния, как правило, носит случайный характер. Однако этот вопрос можно решить, исходя из оценки общей погрешности экспери­мента. При этом должно учитываться следующее. Увеличение интервала варьирования ∆ Х ведет к уменьшению относительной погрешности измерения X; но, с другой стороны, это вызывает

неизбежное увеличение погрешности отнесения, вследствие откло­нения среднего значения измеряемого параметра в интервале варь­ирования Х₁ - Х₂ от его истинного значения, отнесенного к сред­нему значению фактора: Следовательно, при вы­боре значения ∆Х, соответствующего минимальной погрешности эксперимента, необходимо учитывать два фактора — погрешность в измерении интервала варьирования и погрешность отнесения. Это позволяет сделать вывод, что остальные факторы, входящие в общую погрешность эксперимента, не зависят от значения ∆ Х и для каждого данного значения исследуемого фактора остаются по­стоянными.

Оптимальный интервал варьирования ∆Х для заданных усло­вий вычисляется по формуле

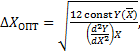(10.4)

где - значение определяющего параметра при среднем зна­чении фактора; const определяется типом контрольно-измеритель­ной аппаратуры.

Для оценки необходимо хотя бы ориентировочно знать Это оказывается невозможным в начале эксперимента. Поэтому выбор возможен лишь после первой стадии экспе­римента, когда будет получена приближенная оценка влияния фактора на зависимую переменную Y.