По результатам многофакторных испытаний

Методы определения характеристик надежности ЭА по резуль­татам многофакторных испытаний принципиально сводятся к ана­лизу следующих двух моделей, отказ изделий в которых является следствием:

■ неблагоприятного соотношения величины ВПО и интенсивно­сти воздействия эксплуатационных факторов;

■ выхода ВПО за данные границы.

Для вычисления характеристик надежности по результатам МФИН в обоих случаях необходимо знать:

■ допустимые пределы значения ВПО 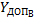и

■ параметры законов распределений внешних воздействий и выходных характеристик ЭА в начальный момент времени их эксплуатации;

■ закон изменения моментных функций ВПС во времени в условиях многофакторных воздействий.

Допустимые предельные значения ВПО задаются в технических условиях на каждый конкретный тип ЭА и поэтому известны экспериментатору. Начальные значения ВПО ЭА непосредственно после их изготовления и установленной приработки при нормальных климатических условиях, отсутствии механических воздействий в нормальных режимах работы имеют обычно гауссовское (нормальное), усеченное нормальное или близкие к ним распределения. Эти начальные значения ВПО можно определить по результатам заводских контрольных и приемо-сдаточных испытаний. Под влиянием внешних факторов, режимов работы, вследствие старения и износа, а также разрегулирования вид закона распределения и его параметры подвергаются изменениям.

Как показывает опыт, встречающиеся на практике закономерности изменения определяющих параметров ЭА во времени близки к линейному или показательному закону. Вместе с тем возможны и другие виды зависимостей определяющих параметров во времени. Например, для описания ухудшения характеристик ЭА во времени используется закон

(10.16)

В общем случае, когда ВПО выражается монотонной функцией времени 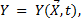плотность вероятности значений параметра связана со скоростью изменения этого параметра и плотностью вероятности f (τ) времени τ, по истечении которого параметр изделия достигает предельного допустимого значения, следующей зависимостью

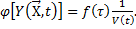(10.17)

При этом вероятность отказа объекта

Случай линейного измерения ВПО во времени. Пусть объект считается исправным, когда значение его ВПО больше границы поля допуска а (рис. 10.2).

Исходя из гипотезы о нормальном законе распределения опреде­ляющего параметра и равномерном линейном виде слу­чайной функции для нормального закона времени безотказной ра­боты плотность распределения составит

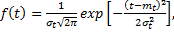(10.18)

где

m_b — математическое ожидание скорости изменения ВПО при воз­действии ; — среднее квадратичное отклонение ВПО в момент времени t = 0 при воздействии факторов .

Таким образом, для равномерной линейной случайной функ­ции 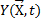вычисление плотности распределения времени безот­казной работы сводится к определению m_t и σ_t по простым форму­лам. Для определения m_t σ_t необходимо знать Значения этих параметров вычисляются на основе резуль­татов МФИН. Например, полагая, что с достаточной для практи­ки точностью зависимость плотности вероятности безотказной работы объекта от действующих факторов внешней среды можно представить полиномом второй степени, составим матрицу пла­нирования второго порядка, в которой в качестве значения функ­ции отклика возьмем значения 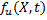(табл. 10.3).

 

 

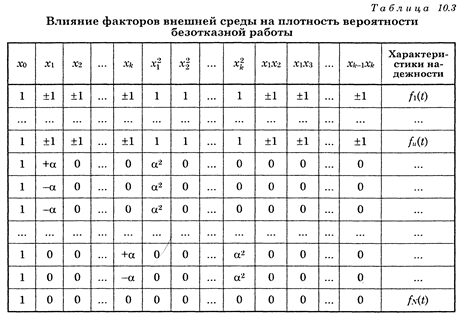
Используя формулы раздела 9.5, определяем коэффициенты уравнения регрессии второго порядка и записываем зависимость показателя надежности объекта от действующих факторов внеш­ней среды в виде

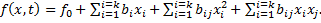(10.19)

Полученная функция показателя надежности дает возмож­ность количественно оценить влияние различных факторов и их взаимодействий на надежность объекта. Кроме того, используя полученную зависимость, можно определить характеристики на­дежности для различных сочетаний факторов, которые в данных испытаниях не воспроизводились.

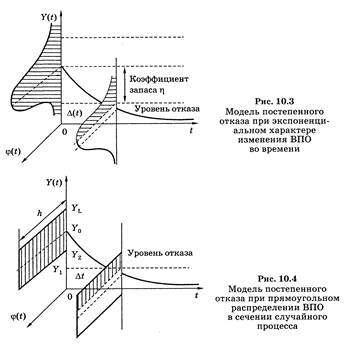
Случай нелинейного изменения ВПО во времени. В случае, когда ВПОизменяется во времени по закону, близкому к экспо­ненциальному (см. рис. 10.3), вероятность безотказной работы объ­екта можно определить следующим образом.

Для упрощения анализа введем прямоугольное распределение определяющего параметра вместо нормального (см. рис. 10.4).

Выбор большого значения коэффициента запаса η позволяет не рассматривать изменение дисперсии распределения характеристик. В наихудшем случае можно предположить, что наибольшая дис­персия в конце испытаний принята для начального состояния. Прямоугольное распределение может быть получено, если учесть, что его интеграл равен единице. Таким образом,

(10.20)

где Y — уровень параметра (начальное значение — Y ₀) с нормиро­ванными верхним и нижним пределами:

Данное нормирование необходимо для того, чтобы среднее значение начального распределения соответствовало значению экспоненты при t = 0. Рассматривая указанные пределы, видим,

что высота нормированного прямоугольного распределения со­ставляет

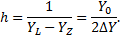
Это прямоугольное распределение имеет фиксированное зна­чение среднего квадратичного отклонения σ_τ, определяемого с по­мощью уравнения

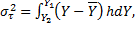(10.21)

в котором предполагается, что

Отличительной особенностью прогнозируемого ухудшения ха­рактеристик ЭА является то обстоятельство, что расположение границ распределения (Y ₀ - ∆ Y)/ Y ₀ над уровнем отказа позволяет осуществить простое вычисление вероятностей появления необ­ходимых значений.

Итак, будем полагать, что ВПО под воздействием комплекса факторов 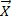во времени t изменяется по закону

где начальное значение Y ₀ и параметры а и b являются случайны­ми величинами, зависящими от условий применения 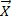. Началь­ный коэффициент запаса исчерпывается, когда достигается зна­чени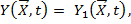е где

(10.22)

Решая уравнение для критического значения времени t _КР, ко­гда работа ЭА перестает быть удовлетворительной, получаем

(10.23)

Для всякого времени, большего, чем t_KP, вероятность нахож­дения характеристик объекта в заданных пределах вычисляется путем определения площади прямоугольника, расположенного выше уровня отказов Таким образом, вероятность нахо­ждения значений характеристики ЭА в заданных пределах после момента времени t_КР:

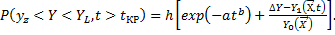(10.24)

Подставляя значение для h и делая преобразования, получаем

(10.25)

Таким образом, дляопределения характеристик надежности ЭА и их зависимости от воздействующих факторов необходимо знать , Нахождение этих величин при воздействии на объект факторов 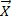производится методами, из­ложенными в главе 9.

Теперь, чтобы записать зависимость показателя надежности объекта от действующих факторов в виде формулы типа (10.19), необходимо составить матрицу планирования, задаваемую таб­лицей вида табл. 10.3, и вычислить коэффициенты уравнения регрессии (10.19).Практически вычисление показателей надеж­ности и их зависимости от действующих факторов сводится, та­ким образом, к выполнению следующей последовательности опе­раций.

1. Определение зависимости ВПО от действующих факторов в начальный момент времени

2. Определение закономерности изменения ВПО во времени
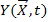и установление зависимости скорости изменения парамет­ра от действующих факторов.

3. Составление матрицы планирования, в которой в качестве функции отклика записывается характеристика надежности ЭА.

4. Реализация матрицы и определение характеристики надеж­ности ЭА для каждого режима испытаний.

5. Вычисление по данным эксперимента коэффициентов урав­нения регрессии.

6. Получение уравнения регрессии, связывающего показатель надежности объекта с действующими факторами.

10.9.

МЕТОДИКА ПЛАНИРОВАНИЯ, ПРОВЕДЕНИЯ И ОБРАБОТКИ РЕЗУЛЬТАТОВ МФИН

1. Выбрать параметры работоспособности объекта (элементов, систем). Основными являются параметры, характеризующие их работоспособность. Предварительно необходимо убедиться в том, что они удовлетворяют следующим условиям:

■ параметры представляют собой независимые, нормально рас­пределенные случайные величины;

■ дисперсии σ² { Y_u }должны быть равны друг другу (выборочные оценки s² { Y_u }однородны).

В случае невыполнения указанных условий произвести преоб­разование случайной величины таким образом, чтобы эти требо­вания выполнялись.

2. На основе анализа предполагаемых условий эксплуатации конкретного типа ЭА логическим путем с использованием данных об эксплуатации аналогичных ЭА в тех же условиях выявить фак­торы, оказывающие значимое влияние на ВПО.

3. При большом их количестве произвести отсеивающие ис­пытания с целью исключения из дальнейшего рассмотрения фак­торов, оказывающих малозначимое влияние на работоспособ­ность ЭА. ^у

4. Для факторов, которые будут выбраны при исследовании их влияния на характеристики надежности, определить рабочие и экстремальные значения, при воздействии которых должны про­водиться испытания, в следующей последовательности:

■ расположить наблюдаемые значения фактора 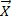по их возрас­танию и получить вариационный ряд величин Х₁, Х₂,..., Х_п;

■ вычислить накопленные частности для каждого интервала ря­да ∆t;

■ вычислить моду М _n и среднее квадратичное отклонение обычным способом;

■ вычислить меру дисперсии а_п и наибольшую вероятную вели­чину μ_п по формулам (10.3).

5. Определить уровни факторов и интервалы их варьирова­ния. За основной (нулевой) уровень фактора следует принять такое его значение, которому соответствует наибольшая плот­ность распределения, т. е. моду М _n. Диапазон изменения фак­тора от основного уровня до экстремального значения разбить
на интервалы, оптимальное значение которых вычислить по формуле (10.4).

6. Произвести нормализацию переменных:

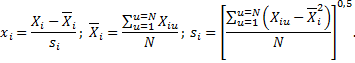
7. Составить матрицу независимых переменных в нормализо­ванном виде.

8. В зависимости от требуемой точности эксперимента и с уче­том п. 7 определить объем выборки по (10.6)...(10.8).

ПОРЯДОК ПРОВЕДЕНИЯ МФИН

Задача определения характеристик надежности ЭА и их зави­симости от действующих факторов разбивается на три этапа:

1. Определение влияния действующих факторов на ВПО.

2. Определение закономерности изменения ВПО.

3. Определение характеристик надежности по результатам многофакторных испытаний.

⇐ Предыдущая40414243444546474849Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: