Анализ отказов электрических аппаратов

На отказ ЭА влияет множество неравнозначных и неоднород­ных факторов, которые связаны с конструкторскими особенностя­ми, технологией изготовления деталей, со сборкой, условиями эксплуатации, режимами работы и т. д. Для оценки влияния этих факторов на показатели надежности используются методы дис­персионного анализа. Эта оценка позволяет осуществить выборку обобщенных факторов, по которым можно судить о функциональ­ных свойствах ЭА и о причинах отклонения технических харак­теристик от заданных норм.

Влияние одного фактора, например уровня эксплуатации на показатели надежности, рассматривается однофакторным диспер­сионным анализом. Выводы или суждения, вытекающие из этого метода, делаются на основе средних оценок результатов испытаний.

Пусть наработку [5] на отказ X приводили на k ЭА одного типа с числом наблюдений на i -м аппарате, равным n_i. Все значения от­казов t _ijфиксировались на каждом из аппаратов (J — номер аппа­рата). Средняя наработка на отказ t_i для каждого i -го ЭА:

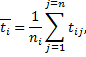
а для k ЭА:

Полученное среднее арифметическое наблюденное значение, согласно постулату Гаусса, является наиболее вероятным значе­нием измеряемого показателя и называется средней наработкой на отказ. Следовательно, среднее арифметическое результатов из­мерений можно считать оценкой истинного математического ожи­дания случайной величины. Однако при малом числе наблюдений отказов среднее арифметическое значение не обеспечивает прием­лемой вероятности. В этом слу­чае делается оценка среднего квадратичного отклонения от истинного значения.

Полное среднее квадратич­ное отклонение случайной вели­чины:

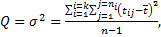(9.20)

где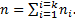

Среднее квадратичное откло­нение между ЭА или рассеяние по фактору

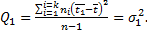(9.21)

Остаточное среднее квадратичное отклонение:

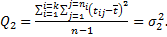(9.22)

При этом Q = Q₁ + Q₂.

Если одновременно рассматривать влияние ряда факторов, та­ких как климатические условия, технический уровень производ­ства, режим эксплуатации, то задача станет многофакторной. Многофакторное исследование эффективнее осуществлять с по­мощью регрессивного анализа.

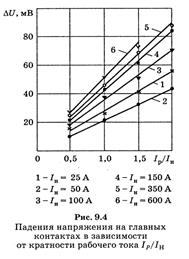
Рассмотрим пример. Эксплуатация контакторов постоянного тока при различных рабочих токах влияет на коммутационную из­носостойкость t через такие факторы, как падение напряжения на главных контактах ∆U, превышение температуры контакта τ, т. е. t = f(∆U, τ). Зависимость падения напряжения на главных контак­тах от кратности рабочего тока I_р / I_н приведена на рис. 9.4.

Как можно видеть, все функции ∆U = f₁(I_p/I_H) имеют линейную зависимость. Причем измеряемая величина падения напряжения на контактах увеличивается с увеличением коммутируемого ра­бочего тока. Одновременно с увеличением падения напряжения наблюдается рост превышения температуры τ контактов в длитель­ном повторно-кратковременном режиме работы контакторов по­стоянного тока.

Зависимость τ от величины кратности рабочего тока представ­лена на рис. 9.5.

В исследуемом диапазоне кратности коммутируемых токов от 0,5 до

4 I _н τ = f₂(I_P/I_H) имеют практически линейный характер. Подставив эти зависимости в t, имеем t = f(I_P/I_H).

Эту функцию представим полиномом регрессии

t = а₁т + а₂т² + а₃т^г +... а_пт^п,

где т = I_P/I_H.

Результат эксперимента проводился при N = 10⁵ циклов ВО. По экспериментальным кривым рис. 9.6 находят коэффициенты регрессии.

Все экспериментальные результаты можно объединить в одну полиномную регрессию. Факторный эксперимент дает возмож­ность численной оценки степени влияния каждого фактора на из­менение функциональных признаков по критерию Стьюдента.

 

РЕКОМЕНДУЕМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧИ

Задача 1. Определить число объектов N, которые необходимо поставить на испытания по плану [ NUM ]при условии, что допусти­мая ошибка в определении Т₀ равна 20% от Т₀ с доверительной ве­роятностью 0,96. Предполагаемая наработка на отказ

Т_о = 1000 ч.

Задача 2. Определить продолжительность испытаний для объ­ектов, обладающих Т₀ = 1000 ч при условии, что вероятность от­каза объекта за время испытания должна быть не меньше 0,9.

Задача 3. Определить число объектов N дляиспытаний, если известно, что σ(t) = 100 ч, распределение Т₀ — нормальное, допус­тимая ошибка — 20 ч, вероятность того, что ошибка определения Т₀ не выйдет за допустимые границы, должна быть не меньше 0,96.

Задача 4. Определить продолжительность испытаний, которые должны подтвердить с доверительной вероятностью 0,9, что Т₀ не ниже 500 ч, если число испытуемых объектов равно 10.

Решение.

1. Для k = 2 и γ = 0,1 значение χ^{2 =} 4,6.

2 .t_p = 0,5 • 500 • 4,6 = 1150 ч.

З.t_u= 1150/10= 115 ч.

Таким образом, если при испытании 10 объектов на протяже­нии 115 ч отказов не будет, то с вероятностью 0,9 можно утвер­ждать, что Е₀ не менее 500 ч.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. По каким признакам классифицируются испытания на надежность?

2. Какие задачи ставятся перед определительными испытаниями на на­дежность?

3. Что такое «план испытаний»?

4. Расскажите о целях контрольных испытаний на надежность.

5. Как вы понимаете испытания, основанные на плане допустимых от­казов, равном нулю?

6. Объясните процедуру проведения испытаний на надежность с исполь­зованием последовательного анализа.

7. В чем состоит необходимость испытаний объектов на надёжность при одновременном воздействии на них эксплуатационных факторов?

8. Расскажите о постановке задачи многофакторных испытаний объ­ектов на надежность.

9. Напишите аналитические выражения для регрессии в векторной и скалярной формах.

10. Как вы понимаете термины «функция отклика» и «параметр опти­мизации»?

11. Что такое «полный факторный эксперимент»?

12. Какие вы знаете критерии оптимальности при планировании много­ факторных испытаний?

 

ОСНОВЫ ИНЖЕНЕРНОЙ МЕТОДИКИ ПЛАНИРОВАНИЯ, ПРОВЕДЕНИЯ И ОБРАБОТКИ РЕЗУЛЬТАТОВ МНОГОФАКТОРНЫХ ИСПЫТАНИЙ

⇐ Предыдущая36373839404142434445Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: