Постановка задачи многофакторных испытаний объектов на надежность

Пусть на объект воздействует комплекс внешних и внутрен­них факторов, который можно представить в виде k -мерного век­тор-столбца:

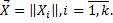
Каждый элемент вектора 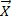отражает влияние какого-либо фактора на объект.

Пространство размерности k, в котором определен вектор 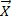, называется факторным пространством или пространством контро­лируемых (независимых) переменных. Это векторное пространст­во обозначим ℜ _k. Совокупность точек пространства ℜ _k, которые могут быть реализованы экспериментатором, называется областью возможных измерений и обозначается 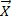. Будем считать, что эле­менты векторного пространства ℜ_к можно умножать только на вещественные действительные величины, т. е. векторное простран­ство ℜ_k — вещественное (действительное) пространство. Опреде­лим в k -мерном векторном вещественном пространстве ℜ_k скаляр­ное произведение (XX)и норму || Х || как

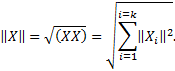
Тогда линейное пространство ℜ_к с фиксированным в нем ска­лярным произведением (XX)и нормой ||Х|| будет евклидовым.

Под воздействием комплекса факторов 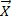в материалах объ­екта протекают физико-химические процессы, вызывающие ста­рение материалов и износ элементов (коррозия и др.). Эти процес­сы могут быть как обратимыми, так и необратимыми. В обоих слу­чаях возможно нарушение состояния работоспособности объекта, т. е. состояния объекта, при котором он способен выполнять за­данные функции с параметрами, установленными требованиями технической документации. Событие, заключающееся в наруше­нии работоспособности, будем называть отказом объекта.

Выходные параметры объекта характеризуются m-мерным век­тором

С учетом того, что факторы внешней сре­ды воздействуют на объект во времени t ∊ T случайным образом, выходные параметры объекта будут представлять собой вектор­ный случайный процесс

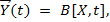(9.15)

где В — оператор воздействий.

Пространство размерности m называется пространством зави­симых переменных. Это пространство, так же как и пространство независимых переменных, будем считать евклидовым.

На основании приведенных рассуждений можно утверждать, что рассматриваемая задача определения показателей надежно­сти объектов сводится к задаче о пересечении непрерывной векторной случайной функцией некоторой заданной (случайной или неслучайной) многомерной допусковой области. В общем случае функция показателя надежности Н(t) связана с вектором 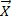дву­мя операторами:

(9.16)

где А — оператор надежности.

Таким образом, задача определения показателей надежности сводится к отысканию некоторым способом двух неизвестных в общем случае операторов А и В.

Остановимся сначала на способе отыскания оператора воздей­ствий В. Рассмотрим наиболее простой случай, когда объект отно­сится к классу объектов с сосредоточенными параметрами и v = 1, т.е. 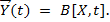При идентификации таких объектов в большин­стве случаев оптимальный оператор ищется по критерию мини­мума средней квадратичной ошибки:

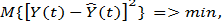(9.17)

где М — оператор математического ожидания; 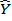— оценка иско­мого параметра объекта.

Известно, что с точки зрения критерия (9.17) оптимальным оператором в классе всех возможных операторов является опера­тор условного математического ожидания, т. е. регрессия выход­ного параметра относительно независимых переменных X и t:

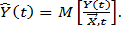(9.18)

Определив по результатам испытаний параметры регрессии, получаем оптимальную (в смысле критерия минимума среднего квадратичного отклонения) оценку оператора воздействий В.

Выбор точек факторного пространства, в которых необходимо проводить испытания, осуществляется методами планирования эксперимента по поиску математической модели или, другими словами, методами планирования эксперимента по выяснению механизма явлений.

Рассматриваемые задачи принадлежат к классу сложных ди­намических задач, где принимаются как строго формализованные, так и интуитивные решения. На каждом этапе исследования вы­бирается в соответствии с определенными критериями оптималь­ное в смысле объема испытаний V расположение точек в фактор­ном пространстве, т. е. операторы А и В отыскиваются при

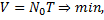(9.19)

где N₀ — число необходимых для испытаний объектов; Т — дли­тельность испытаний.

С простейшими методами планирования многофакторных ис­пытаний для сложных объектов, а также и для ЭА, можно познако­миться в опубликованной литературе (см., например, [11, с. 278]).