Случайных величин по эксплуатационной информации

Известно, что для полной характеристики любой случайной величины необходимо знать ее закон распределения в виде функ­ции распределения (в нашем случае вероятности отказа) или плот­ности вероятности. Определение закона распределения отказов (или восстановлений) по опытным данным, т. е. по выборке, осу­ществляется в три этапа.

1. Выбор вида закона распределения. Подбор для данного ста­тистического ряда теоретической кривой распределения и нахож­дения ее параметров в статистике называют выравниванием (сгла­живанием) статистических рядов. Основой выравнивания являет­ся выбор вида теоретической кривой распределения. При принятии гипотезы о виде теоретического распределения главным является понимание характера причин утраты работоспособности ЭА. Дру­гими словами, вид теоретического распределения, как правило, должен выбираться заранее из соображений, связанных с сущно­стью рассматриваемых явлений. Экспериментальными данными подтверждается хорошее соответствие процессов, приводящих к внезапным отказам, экспоненциальному закону распределения, процессов чистого износа — нормальному закону. Процессы уста­лостного разрушения, а также процессы, представляющие собой совокупность видов разрушения (усталостного, износа, внезапных изменений свойств объекта и др.), могут быть описаны распреде­лением Вейбулла. Универсальность применения распределения Вейбулла в задачах надежности обусловливается широкими воз­можностями вариации его формы. При выборе теоретического закона распределения необходимо помнить, что для выявления статистически значимых различий законов распределения тре­буется большой объем информации, особенно для использования двух и более параметрических законов. Ориентировочно закон рас­пределения можно выбрать по виду аппроксимации статистиче­ского ряда.

2. Проверка согласия опытного распределения с теоретиче­ским осуществляется с помощью критериев согласия Колмогоро­ва, Пирсона, χ², ω² и др.

После выбора теоретического закона распределения приступа­ют к определению оценок неизвестных параметров закона распре­деления и количественных показателей надежности. Оценкой па­раметра называется его значение, найденное по выборке, т. е. по ограниченному числу наблюдений. Если оценкой параметра яв­ляется число, то такие оценки называются точечными. Если же оценкой служит совокупность чисел (интервал на числовой оси), то оценки называются интервальными. Существует несколько методов получения оценок неизвестных параметров 0 закона рас­пределения генеральной совокупности по выборке

Наи­более распространенными являются метод моментов и метод мак­симального правдоподобия.

При использовании метода моментов параметры θ выбирают­ся таким образом, чтобы несколько важнейших числовых харак­теристик (моментов) теоретического распределения были равны соответствующим моментам выборки. Для дискретных случайных величин X моменты

(11.1)

(11.2)

где — соответственно начальные и центральные моменты s -гo порядка; p_i — вероятность того, что случайная величина при­мет i -e значение; a_s, m_s — соответственно статистические (выбо­рочные) начальные и центральные моменты.

Например, если теоретическая кривая f(x) зависит только от двух параметров (нормальное распределение, закон равномерной плотности), то эти параметры выбираются так, чтобы математи­ческое ожидание М[Х] и дисперсия D[X] теоретического распре­деления совпадали с соответствующими моментами выборки a_s и m_s. Характерной особенностью метода моментов является воз­можность его применения без каких-либо предположений о виде закона распределения случайной величины (требуется лишь су­ществование моментов соответствующих порядков).

Метод максимального правдоподобия требует для применения предварительного знания вида закона распределения; значение же параметров θ, входящих в аналитическое выражение этого зако­на, считается неизвестным. Согласно методу максимального прав­доподобия в качестве оценки θ * (x_i)параметра θ выбирается такая функция от наблюдений которая достигает максимума функции

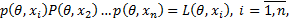(11.3)

называемой функцией правдоподобия. Если при θ = θ*(х _i) функ­ция правдоподобия достигает наибольшего значения, то при этом же θ достигает наибольшего значения и функция lnL(θ, x_i). Для отыскания оценок максимального правдоподобия нужно решить уравнения

(11.4)

В силу ограниченности выборки одному и тому же параметру закона распределения может быть поставлено в соответствие мно­жество его оценок — как точечных, так и интервальных. С целью выбора такой оценки параметра, чтобы ошибки по возможности были минимальными, применяется ряд критериев: оценка должна быть состоятельной, несмещенной, эффективной и достаточной.

В качестве оценки математического ожидания а (генерально­го среднего) обычно используется среднее выборочное

(11.5)

являющееся несмещенной оценкой генерального среднего для любого распределения. Для нормального закона среднее является также состоятельной, эффективной и достаточной оценкой. Для дисперсии σ² в случае неизвестного генерального среднего несме­щенная оценка имеет вид

(11.6)

Оценками начальных моментов α_s и центральных моментов μ_s s -гo порядка генеральной совокупности служат соответствующие выборочные моменты, определяемые по формулам (11.1) и (11.2). Начальные моменты a_s являются состоятельными несмещенными оценками моментов α_s, центральные моменты m_s — состоятельны­ми, но смещенными оценками моментов μ_s.

Если в результате наблюдений получена выборка наработки на отказ то оценка средней наработки на отказ и средне­го квадратического отклонения находится по формулам

(11.7)

Точечные оценки количественных показателей надежности при экспоненциальном законе распределения наработки и време­ни восстановления можно получить из выражений:

 

(11.8)

Истинные значения оцениваемых величин будем далее обозна­чать

Интервальная оценка параметров закона распределения пред­ставляет собой случайный интервал, который с некоторой вероят­ностью накрывает оцениваемый параметр θ. Этот интервал назы­вается доверительным, его границы — доверительными, вероят­ность, с какой доверительный интервал накрывает параметр θ, — доверительной вероятностью. Для заданной вероятности а по вы­борке случайной величины X могут быть найдены зна­чения случайных величин θ_Н и θ_В, при которых:

1) интервал от θ_Н до +∞ накроет параметр θ с вероятностью

2) интервал от -∞ до θ_В накроет параметр θ с вероятностью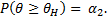

Величины θ_Н и θ_B являются, соответственно, нижней и верх­ней доверительной границей для параметра θ; θ_Н и θ_В образуют до­верительный интервал для параметра θ при двусторонней довери­тельной вероятности а, определяемой по формуле а = α₁ + α₂ при 0,5 < α₁ < 1, 0,5 < α₂ < 1. В общем виде эта зависимость имеет вид 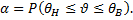При этом, чем больше доверительная вероят­ность а, тем шире границы интервала, и наоборот. Вероятность того, что значение θ выйдет за границы интервала (θ_Н, θ_В), назы­вается уровнем значимости

Значения доверительных вероятностей обычно принимают рав­ными 0,9; 0,95; 0,99. Соответствующие им уровни значимости со­ставляют 0,1; 0,05; 0,01.

3. Интервальная оценка показателей надежности при экспо­ненциальном законе распределения. Оценки показателей надеж­ности могут быть получены по результатам эксплуатации большо­го числа объектов усреднением по множеству или небольшого чис­ла объектов усреднением по времени, т. е. необходимо иметь либо большое число отказов либо время эксплуатации Т, стре­мящееся к бесконечности

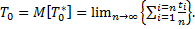(11.9)

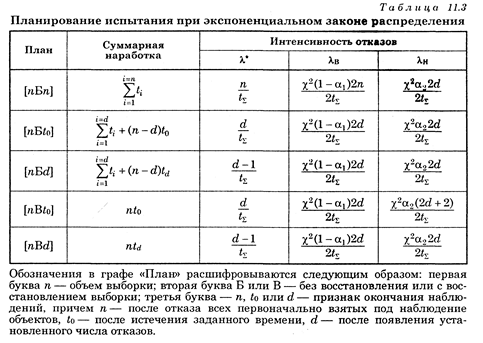
При реальной эксплуатации сложных ЭА Поэто­му точечные и интервальные оценки показателей надежности ЭА зависят от плана испытаний. В табл. 11.3 приведены формулы рас­чета точечной (средней) оценки интенсивности отказов, а также нижней и верхней границ интенсивности отказов λ_H и λ_B для раз­личных планов испытаний.

Для определения границ λ необходимо пользоваться таблицей квантилей χ²-распределения, в которой даются доверительные ве­роятности (1 – α₁)или α₂ и число степеней свободы k, равное 2п, 2d или 2d + 2 в зависимости от выбранного плана. Для двустороннего интервала доверительная вероятность α₁ = α₂ = 0,5(1 + d). Значение а задается в зависимости от требований, предъявляемых к системе.

Используя табл. 11.3, можно рассчитать значения показате­лей надежности при экспоненциальном законе распределения

(11.10)

Например, интервальная оценка показателей надежности при нормальном законе распределения производится в зависимости от того, известны или неизвестны значения среднего идисперсии ге­неральной совокупности.

Пусть известен объем выборки наработки на отказ. При неизвестной дисперсии генеральной совокупности дове­рительные границы для Т₀ определяются следующим образом:

(11.11)

где ε — заранее заданный интервал;

Значения ε находятся из выражения

(11.12)

где s — оценка среднего квадратического отклонения; — квантиль распределения Стьюдента, который находится в табли­цах по заданной доверительной вероятности α и числу степеней свободы n - 1

где φ(t) — плотность вероятности распределения Стьюдента.

 

⇐ Предыдущая40414243444546474849

Поделиться:

Воспользуйтесь поиском по сайту: