 |
Проекция силы на ось и на плоскость
|
|
|
|
Теорема о трех силах
Теорема. Три непараллельные силы, ле-жащие в одной плоскости, могут нахо-диться в равновесии только если линии их действия пересекаются в одной точке.
На рис. показана система трѐхуравнове-шенных сил и, причем линии дей-ствия сил и пересекаются в точке А.
Воспользуемся аксиомами III и IV, т.е. пе-ренесѐм силы и в точку А и найдѐм их равнодействующую. Тогда заданная система трѐх сил, будет эквивалентна системе двух сил и. Эта система (по аксиоме III) может находиться в рановесии только если силы и будут лежать на одной пря-мой. Следовательно, линия действия силы тоже должна проходить через точку А. 
52 вопрос
В прямоугольной системе координат XYZ (рис. 2.1) сила 
задается модулем 
, углами QUOTE α, β, γ 
, образованными силой с осями координат и точкой приложения силы (точка А). Положение точки Аопределяется координатами 
. Углы QUOTE α, β, γ называются направляющими углами. Проекция силы на каждую координатную ось равна произведению модуля силы на косинус направляющего угла:
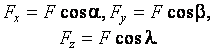(2.1)
Если же заданы проекции силы 
, то модуль силы и косинусы направляющих углов определятся по
следующим формулам:
Геометрический способ сложения сил. Геометрическая сумма (главный вектор) системы сил F1, F2,..., Fn определяется построением силового многоугольника. Для этого пользуются правилом сложения векторов. В произвольной точке О вектор R, соединяющий начало первого вектора F1 с концом последнего Fn изображает геометрическую сумму или главный вектор слагаемых сил:
R = F1 + F2 +... + Fn = SFk. (k = 1, 2,.., n)
. 
Проекцией силы на ось называется алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси:
|
|
|
Fх = |F|Чcosa.
Fх > 0, если 0 <a<p/2; Fх< 0, если p/2 <a<p; Fх = 0, если a = p/2.
Проекция силы на ось и на плоскость
Перейдем к рассмотрению аналитического (численного) метода решения задач статики. Этот метод основывается на понятии о проекции силы на ось. Как и для всякого другого вектора, проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак плюс, если перемещение от ее начала к концу происходит в положительном направлении оси, и знак минус - если в отрицательном. Из определения следует, что проекции данной силы на любые параллельные и одинаково направленные оси равны друг другу. Этим удобно пользоваться при вычислении проекции силы на ось, не лежащую в одной плоскости с силой.
Обозначать проекцию силы F на ось Ох будем символом. Тогда для сил, изображенных на рисунке, получим:
.
Но из чертежа видно, что AВ1=F cosα, ЕD1=Q cosβ=-Q cosα1.
Следовательно,
, 
.
т. е. проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси. При этом проекция будет положительной, если угол между направлением силы и положительным направлением оси - острый, и отрицательной, если этот угол - тупой; если сила перпендикулярна к оси, то ее проекция на ось равна нулю.
Проекцией силы F на плоскость Oxy называется вектор, заключенный между проекциями начала и конца силы F на эту плоскость. Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только своим численным значением, но и направлением в плоскости Oxy. По модулю Fxy=F cosθ, где θ — угол между направлением силы F и ее проекции Fxy. В некоторых случаях для нахождения проекции силы на ось бывает удобнее найти сначала ее проекцию на плоскость, в которой эта ось лежит, а затем найденную проекцию на плоскость спроектировать на данную ось. Например, в случае, изображенном на рисунке, найдем таким способом, что
|
|
|
Способ двойного проецирования.
Суть способа состоит в том, что вначале находят проекцию силы на плоскость, в которой эта ось расположена, а затем – проекцию полученного вектора на ось. Так, для определения проекций силы 
на оси 
(рис. 2.1) вначале находим проекцию силы на плоскость xOy и получаем вектор 
, а затем
; 
.
Проекцию силы на ось z находим по обычному правилу, т.е. 
.
Вопрос
|
|
|
