Лемма о параллельном переносе силы

Докажем лемму: Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Пусть в точке А твердого тела приложена сила F (рис. 4.1). Приложим теперь в точке В тела систему двух сил F' и F²-, эквивалентную нулю, причем выбираем F'=F (следовательно, F"=–F). Тогда сила F~(F, F', F"), так как (F',F")~0. Но, с другой стороны, система сил (F, F', F") эквивалентна силе F' и паре сил (F, F"); следовательно, сила F эквивалентна силе F' и паре сил (F, F"). Момент пары (F, F") равен M=M(F,F")=BAxF, т.е. равен моменту силы F относительно точки В M=M_B(F). Таким образом, лемма о параллельном переносе силы доказана.

 

64 вопрос

Приведение плоской системы сил к данному

Центру. Теорема Пуансо

 

Пусть к твердому телу приложена плоская система сил 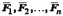(рис.1.16). Возьмем в теле произвольную точку , ко­торую будем называть центром приведения, и приложим к ней по­парно уравновешенные силы и . Заметим, что силы и образуют при этом пару сил, так что можно считать силу 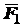перенесенной параллельно самой себе в точку 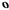- за­мененной силой 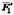с присоединением пары . 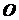Посту­пив так и со всеми оставшимися силами, мы приведем заданную систему сил к совокупности пучка сил , приложенных в точке , и совокупности пар 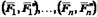. Сходящиеся силы имеют равнодействующую 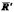, приложенную в точке и равную векторной сумме всех сил системы. Эта сумманазывается главным век­тором системы и обозначается .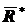

Пары можно заменить одной результирующей парой с моментом 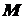, равным алгебраической суммеих моментов. Так как момент пары равен сумме момен­тов входящих в нее сил относительно любой точки плоскости пары, то для каж­дой из складываемых пар

.

Поэтому сумма моментов пар равна сумме моментов самих заданных сил отно­сительно точки 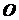, которая называется главным момен­том системы относи­тельно этой точки и обозначается . Та­ким образом, систему сил, произ­вольно расположенных на плоско­сти, можно заменить совокупностью одной силы 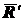, равной их главному вектору 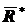, и приложенной в произвольно выбран­ном центре приведения, и одной пары, момент которой 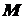равен главному мо­менту заданных сил относительно центра приве­дения. Это утверждение на­зывается теоремой Пуансо о приведении плоской системы сил к данному цен­тру.

Главный вектор и главный момент системы опре­деляются по формулам:

(1.5)

Главный вектор и главный момент плоской системы сил

Рассмотрим плоскую систему сил (F ₁, F ₂,..., F _n),действующих на твердое тело в координатной плоскости Oxy.

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

R = F ₁ + F ₂ +... + F _n = F _i.

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор L _O, равный сумме векторных моментов этих сил относительно точки О:

L _O = M _O(F ₁) + M _O(F ₂) +... + M _O(F _n) = M _O(F _i).

Вектор R не зависит от выбора центра О, а вектор L _O при изменении положения центра О может в общем случае изменяться.

Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом L_O плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра О.

Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.

Пример. К вершинам квадрата со стороной a = 0.5(м) приложены силы: F₁ = 4(Н); F₂ = F₃ = 8(Н); F₄ = 12(Н). Определить главный вектор этой системы сил и ее алгебраический главный момент относительно центра квадрата О.

Решение. Введем координатную систему Oxy, оси которой параллельны сторонам квадрата (в такой системе координат расчеты проводятся наиболее простым образом).

Силы F ₂, F ₃ образуют пару сил с моментом M₂₃ = -F₂·a=-4(Н·м) и их можно не учитывать при вычислении проекций главного вектора R:

R_х = F_1x + F_4x = -F₁ + F₄= -4 + 12 = 8(Н);

R_y = F_1y + F_4y = 0.

Вычисление алгебраического главного момента L_O проведем с использованием плеч сил F ₁ и F ₄, равных половине длины стороны квадрата (a/2):

L_O = F₁·a/2 - F₄·a/2 + M₂₃ = 1 - 4 + 3 = 0.

Таким образом, для заданной системы сил ее главный вектор равен по модулю R = 8(Н) и направлен вдоль оси Ox, а ее алгебраический главный момент L_O = 0.

Замечание. В случае, когда L_O = 0, главный вектор R является равнодействующей силой заданной системы сил.

 

65 вопрос

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: