 |
Точечные и интервальные оценки
|
|
|
|
Результат испытаний может быть дискретной или непрерывной случайной величиной. Так, количество дефектных изделий в выборке - дискретная случайная величина, поскольку это может быть только целое число.
Непрерывная случайная величина может принимать любое значение в некотором конечном или бесконечном интервале (например, разрывная длина бумаги). При испытаниях часто получают выборку значений непрерывной случайной величины с некоторым распределением вероятности получения того или иного значения. Наиболее часто встречается нормальное распределение. Точнее, реальные распределения в большинстве случаев достаточно близки к нормальному.
Основные параметры нормального распределения – математическое ожидание М случайной величины и её генеральное среднее квадратичное отклонение (СКО) σ (или генеральная дисперсия σ2). Математическое ожидание – это центр группировки результатов испытаний, при отсутствии систематических погрешностей соответствует количественной характеристике объекта испытаний. Дисперсия (или СКО) – мера рассеяния результатов испытаний. Найти их значения абсолютно точно невозможно. Однако при объёме выборки n не менее 25…30 обычно считают, что точечные оценки параметров нормального распределения с приемлемой точностью равны параметрам. Кроме того, можно достаточно точно рассчитать генеральную дисперсию при проведении серий испытаний, в которых генеральная дисперсия не меняется (вычисление дисперсии по текущим измерениям), например, при приёмо-сдаточных испытаниях.
Применяется также мера рассеяния, называемая коэффициентом вариации. Генеральный коэффициент вариации
γ = М/σ. (1.1)
|
|
|
Выборочный коэффициент вариации
(1.2)
Точечной оценкой математического ожидания М является среднее значение выборки 
(В Excel функция СРЗНАЧ):
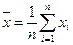
Точечной оценкой генеральной дисперсии является выборочная несмещенная дисперсия (функция ДИСП):
По текущим измерениям дисперсия может быть вычислена по формуле 
Здесь ni – объем испытаний (объём выборки) в каждой серии, si2 – дисперсии в соответствующих сериях, m – количество серий.
Оценка генерального СКО - выборочное СКО (функция СТАНДОТКЛОН):
Точечные оценки малоинформативны, поскольку являются случайными величинами и могут значительно отличаться от оцениваемого параметра. Для повышения информативности используют интервальные оценки (рассчитывают доверительные интервалы).
При достаточно точно известной генеральной дисперсии σ2 доверительный интервал для математического ожидания определяют из соотношения
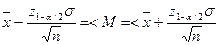(1.3)
или 
Здесь уровень значимости a=1-Р (Р -доверительная вероятность), z1-α/2 – квантиль стандартного нормального распределения (функция НОРМСТОБР), n – объём испытаний (объём выборки).
Если генеральная дисперсия неизвестна, доверительный интервал для математического ожидания определяют из соотношения
Здесь tα,к – коэффициент Стьюдента (СТЬЮДРАСПОБР), k=n-1 – число степеней свободы.
Доверительный интервал для дисперсии определяют из соотношения:
Здесь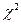 
- критерий распределения хи-квадрат (функция ХИ2ОБР), k=n-1 – число степеней свободы.
Извлекая из всех частей неравенства квадратный корень, можно получить интервальную оценку СКО.
Пример 1.1. Проведены испытания на разрыв образцов дюралюминиевого профиля. Полученные значения предела прочности образцов (МПа) приведены в табл. 1.1.
Таблица 1.1.
Найти точечные и интервальные оценки параметров распределения предела прочности при доверительной вероятности 0,95.
|
|
|
Фрагмент выполнения примера 1.1 показан на рис.1.1.
Открываем новую книгу программы Excel и переименовываем Лист 1 в Задание 1, открыв контекстное меню (правой кнопкой мыши) на яр лыке с названием листа и выбрав команду Переименовать. В ячейку А1 вводим заголовок работы Лаб. работа 1. Точечные и интервальные оценки.
Рис.1.1. Фрагмент расчёта для примера 1.1.
В ячейки В4:В33 вводим значения предела прочности, в ячейки А4:А33 номера соответствующих данных. В ячейке Е3 рассчитываем объём испытаний (объём выборки) функцией СЧЁТ. При этом в диалоговом окне функции СЧЁТ в строке Значение 1 вводим интервал от В4 примерно до В1000, не до В33. Это необходимо для того, чтобы электронная таблица была пересчитываема, т.е. при последующем введении других данных в другом количестве (большем или меньшем) все расчётные значения автоматически пересчитывались бы для этих новых данных. Так следует поступать и при использовании других функций.
В ячейку Е4 вводим значение доверительной вероятности. В ячейке Е5 рассчитываем уровень значимости (но не вводим в виде числа, чтобы при другой доверительной вероятности таблица автоматически пересчитывалась).
В ячейках Е7, Е8 и Е9 соответственно рассчитываем среднее значение предела прочности, его СКО и дисперсию по соответствующим статистическим формулам (поставьте размерности). В ячейках D11:D13 и F11:F13 рассчитываем соответственно нижние и верхние границы доверительных интервалов для математического ожидания, дисперсии и СКО. При этом, учитывая, что объём испытаний достаточно велик, т.е. σ ≈ s, границы доверительного интервала для математического ожидания рассчитываем по формуле (1.3). При получении значений z и χ2 в диалоговых окнах функций НОРМСТОБР и ХИ2ОБР значения вероятностей следует получать расчётом со ссылками на ячейку со значением α, а не вводить в виде чисел, чтобы таблица была пересчитываемой. (Внимание! Адреса ячеек вводить в формулы и строки диалоговых окон следует путём указания мышью на эти ячейки., но не вводом с клавиатуры, который замедляет работу и увеличивает вероятность ошибок).
Примечания:
|
|
|
1. Величину доверительного интервала, в виде возможного при данном уровне значимости отклонения от среднего выборки, можно вычислить также при помощи статистической функции ДОВЕРИТ.
2. Чтобы ввести в ячейке часть текста в виде верхнего или нижнего индекса, следует в строке формул выделить необходимую часть текста, затем задать для неё верхний индекс командой Формат – Ячейки и отметкой в диалоговом окне Верхний индекс.
Задание.
1. Выполнить расчёты в соответствии с примером 1.1. Как изменяются доверительные интервалы (увеличиваются или уменьшаются) при уменьшении доверительной вероятности?
2. Найти точечные и интервальные оценки математического ожидания, дисперсии и СКО некоторой характеристики (табл. 1.2), полученной по результатам испытаний.
3. По результатам испытаний выборок из четырёх партий бумаги получены значения разрывной длины образцов бумаги, представленные в табл. 1.3.
Определить дисперсию по результатам испытаний всех партий (по текущим измерениям), учитывая, что генеральная дисперсия в разных партиях не меняется. Для партии 4 определить доверительный интервал для математического ожидания, используя рассчитанную дисперсию как генеральную, при доверительной вероятности 0,9.
Таблица 1.2.
| Вариант | Р | Значения характеристики | |||||||||
| 0,95 | 15,9 | 18,3 | 16,5 | 17,9 | 16,3 | 18,2 | 16,9 | 17,6 | 16,0 | 16,5 | |
| 0,90 | 7,41 | 7,50 | 7,25 | 7,63 | 7,55 | 7,66 | 7,43 | 7,38 | - | - | |
| 0,99 | - | ||||||||||
| 0,98 | 53,8 | 53,1 | 54,3 | 54,6 | 56,4 | 54,6 | 56,0 | 55,3 | 55,0 | 54,4 | |
| 0,97 | - | ||||||||||
| 0,95 | 5,6 | 5,7 | 5,8 | 5,4 | 5,9 | 5,6 | 5,5 | 5,7 | 5,5 | 5,7 | |
| 0,90 | 0,55 | 0,58 | 0,57 | 0,56 | 0,54 | 0,59 | 0,56 | 0,56 | - | - | |
| 0,99 | 8,5 | 8,7 | 8,3 | 8,7 | 8,7 | 8,9 | 8,4 | 8,9 | 9,0 | 8,6 | |
| 0,98 | 7,33 | 7,31 | 7,35 | 7,28 | 7,45 | 7,25 | 7,42 | - | - | ||
| 0,97 | 7,51 | 6,43 | 6,34 | 7,38 | 6,96 | 7,10 | 6,88 | 7,52 | 6,56 | 6,77 |
Таблица 1.3.
| Партия | Номер образца | |||||||||
| Разрывная длина, м | ||||||||||
| - | - | |||||||||
| - |
|
|
|
Лабораторная работа № 2
|
|
|
