Проверка приемлемости результатов испытаний

При проведении испытаний широко распространено получение двух результатов (двух параллельных определений). При этом приемлемость результатов испытаний может проверяться для условий повторяемости или повторяемости и воспроизводимости одновременно.

Повторяемость (сходимость) - это близость результатов испытаний одного и того же объекта, полученных по одной методике в одной и той же лаборатории одним и тем же оператором на одном и том же оборудовании за короткий промежуток времени.

Предел (норматив) повторяемости r = 2,8s_r, где s _r, - среднеквадратическое отклонение, полученное в условиях повторяемости.

Воспроизводимость- это близость результатов испытаний одного и того же объекта, полученных по единым методикам с применением различных экземпляров оборудования разными операторами в разное время, т.е. в разных лабораториях.

Предел воспроизводимости R = 2,8s_R где s _R, - среднеквадратическое отклонение, полученное в условиях воспроизводимости.

Численные значения r и R указываются в методах испытаний.

При проверке приемлемости результатов испытаний, полученных в условиях повторяемости, поступают так:

Если | x₁ - x₂ | ≤ r,где x₁ и x₂ - два результата испытаний, полученные в условиях повторяемости, то окончательный результат равен среднему арифметическому.

Если | x₁ - x₂ | > r, лаборатория должна получить ещё два результата, если это не является дорогостоящим. Если при этом для четырёх результатов x_max - x_min ≤ CR_0,95(4), то за окончательный результат берут среднее арифметическое этих четырёх результатов. Если для четырёх результатов испытаний x_max - x_min > CR_0,95(4), то за окончательный результат берут медиану этих результатов.

Здесь CR_0,95(4) - критический диапазон для уровня вероятности 95 % и n = 4.

CR_0,95(n) = f(n)∙s_r= f(n)∙r/2,8

Коэффициенты f (n) указаны в табл. 3.1.

Таблица 3.1

n	f (n)	n	f (n)
	2,8		5,2
	3,3		5,2
	3,6		5,2
	3,9		5,3
	4,0		5,3
	4,2		5,3
	4,3		5,3
	4,4		5,3
	4,5		5,4
	4,6		5,4
	4,6		5,4
	4,7		5,4
	4,7		5,4
	4,8		5,5
	4,8		5,5
	4,9		5,5
	4,9		5,6
	5,0		5,6
	5,0		5,8
	5,0		5,9
	5,1		5,9
	5,1		6,0
	5,1		6,1

Если испытания дорогостоящие и по двум результатам |x₁ - x₂|>r, надо получить ещё один результат испытаний. Если при этом по трём результатам x_max - x_min ≤ CR_0,95(3), то за окончательный результат берут среднее арифметическое этих трёх результатов. Если x_max - x_min > CR_0,95(3) и невозможно получить четвёртый результат испытаний, то за окончательный результат принимают медиану трёх результатов.

Пример 3.1. В лаборатории проведены испытания автомобильного бензина марки АИ-93 на соответствие требованиям ГОСТ 2084-77 по показателю «октановое число по исследовательскому методу» по ГОСТ 8226-82, в котором установлено значение r = 0,5. Получены результаты х₁ = 93,4 и х₂ = 93,0. Проверить приемлемость результатов и найти окончательный результат.

Вариант выполнения примера 3.1 показан на рис.3.1.

 

Рис.3.1. Вариант расчёта для примера 3.1

 

Для вывода сообщения в ячейке С8 используем функцию ЕСЛИ. В её диалоговом окне вводим логическое выражение | x₁ - x₂ |£ r (разумеется, вместо ввода символов надо сделать ссылки на соответствующие ячейки), В строку Значение_если_истина вводим сообщение «Результаты приемлемы», в строку Значение_если_ложь – сообщение «Результаты неприемлемы. Получите ещё 2 результата». Поскольку логическое выражение истинно, в ячейке С8 появится сообщение «Результаты приемлемы».

Пример 3.2. Предположим, что в условиях предыдущего примера х₁ = 93,6 и х₂ = 93,0.. Введя эти значения в электронную таблицу, убедимся, что результаты неприемлемы, и надо получить ещё два результата. Пусть получены результаты х₃ = 93,2 и х₄ = 92,8. Скопируем электронную таблицу на новый лист электронной книги и модифицируем её, как показано на рис. 3.2.

 

Рис.3.2. Вариант расчёта для примера 3.2.

 

Здесь рассчитываем среднее значение и медиану (функция МЕДИАНА) четырёх результатов. Окончательный результат выводим с помощью функции ЕСЛИ, используя логическое выражение x_max - x_min ≤ CR_0,95(4). В зависимости от истинности или ложности этого выражения окончательный результат будет равен среднему значению или медиане.

Проверка результатов испытаний, полученных в условиях как повторяемости, так и воспроизводимости, т.е. в двух лабораториях, может быть необходима при возникновении спорных ситуаций между поставщиком и заказчиком. Здесь возможны два случая:

1). Когда каждая лаборатория получила только один результат испытаний. Если при этом | X₁ - X₂ |£ R, за результат принимают среднее арифметическое X₁ и X₂, где X₁ и X₂ – два результата, полученные в условиях воспроизводимости, т.е. в разных лабораториях.

Если | X₁ - X₂ |> R, следует выяснить, чем обусловлено расхождение: низкой повторяемостью метода испытаний и/или различием в испытываемых пробах (образцах). Для этого проверяют повторяемость результатов в обеих лабораториях.

Пример 3.3. В двух лаборатории проведены испытания автомобильного бензина марки АИ-93 на соответствие требованиям ГОСТ 2084-77 по показателю октановое число по исследовательскому методу по ГОСТ 8226-82, в котором установлены значение R = 1,0. В каждой лаборатории получено по одному результату Х₁ = 93,6 и Х₂ = 93,0. Проверить приемлемость результатов и найти окончательный результат.

Создать пересчитываемую электронную таблицу по данным примера можно, модифицировав на новом листе электронной книги таблицу, созданную в примере 3.1.

2). Когда каждая из двух лабораторий получает более одного результата испытаний (параллельных определений), т.е. каждая лаборатория получит свой окончательный результат. При этом необходимо проверить взаимоприемлемость (совместимость) этих двух окончательных результатов. Для этого сравнивают | X₁ - X₂ | с критической разностью CD_0,95, где X₁ и X₂ - окончательные результаты испытаний в двух лабораториях. Если | X₁ - X₂ | ≤ CD_0,95, приемлемы оба результата, и в качестве окончательного можно использоваться их общее среднее значение. Если | X₁ - X₂ | > CD_0,95, то противоречия между результатами двух лабораторий разрешают по определённым процедурам, например, меняя образцы между лабораториями, приглашая арбитражную лабораторию и др.

В зависимости от того, получены ли X₁ и X₂ как средние значения или как медианы параллельных определений, CD_0,95 рассчитывают по формулам:

а). Для двух средних арифметических значений

Здесь n₁ и n₂ – количество результатов испытаний в двух лабораториях.

б). Для среднего арифметического из n₁ и медианы из n₂

Значения c (n) – представлены в табл. 3.2.

Таблица 3.2.

Количество результатов испытаний n	c (n)
	1,000
	1,000
	1,160
	1,092
	1,197
	1,135
	1,214
	1,160
	1,223
	1,176
	1,228
	1,187
	1,232
	1,196
	1,235
	1,202
	1,237
	1,207
	1,239
	1,212

в). Для двух медиан

Пример 3.4. В двух лаборатории проведены испытания автомобильного бензина марки АИ-93 на соответствие требованиям ГОСТ 2084-77 по показателю октановое число по исследовательскому методу по ГОСТ 8226-82, в котором установлены значения r = 0,5 и R = 1,0. Получены результаты соответственно Х₁ = 93,4 и Х₂ = 93,0. Результат Х₁ получен как среднее из двух параллельных определений, результат Х₂ – как медиана из четырёх параллельных определений. Проверить взаимоприемлемость результатов и найти окончательный результат.

Вариант выполнения примера 3.4 показан на рис.3.3.

 

Рис.3.3. Вариант расчёта для примера 3.4

 

Вводим исходные данные. При этом результат, полученный как среднее, кодируем значением 0, а результат, полученный как медиана, кодируем значением 1. Результат, полученный как среднее, приписываем лаборатории с условным номером 1, чтобы в дальнейшем была определённость при расчёте значения CD_0,95.

Далее вводим таблицу значений c(n) и находим значение с(n) для каждой из лабораторий, используя функцию ИНДЕКС. На первом шаге выбираем Массив;номер_строки;номер_столбца. На втором шаге в диалоговом окне функции ИНДЕКС в качестве массива указываем диапазон значений с(n),а также ссылки на номер строки и номер столбца в массиве. Номер строки – это количество параллельных определений для данной лаборатории, номер столбца равен 1, т.к. столбец в массиве значений с(n) один.

Затем рассчитываем значения CD_0,95 для двух средних, для среднего и медианы и для двух медиан. Выбираем из этих значений то, которое соответствует данному случаю. Для этого используем функцию ЕСЛИ, в диалоговом окне которой вводим логическое выражение C10+D10=0, что будет соответствовать случаю, когда результаты в обеих лабораториях получены по средним значениям параллельных определений. Поэтому в строке Значение_если_истина ссылаемся на ячейку со значением CD для этого случая. В строку Значение_если_ложь, снова вводим функцию ЕСЛИ. В открывшемся при этом новом диалоговом окне вводим логическое выражение C10+D10=1, что будет соответствовать случаю, когда результаты в разных лабораториях получены по среднему и по медиане параллельных определений. В строку Значение_если_истина нового диалогового окна ссылаемся на ячейку, содержащую значение CD для этого случая. В строке Значение_если_ложь второго диалогового окна вводим снова функцию ЕСЛИ, и в открывшемся третьем диалоговом окне вводим логическое выражение C10+D10=2, что будет соответствовать случаю, когда результаты в обеих лабораториях получены по медианам параллельных определений. В строке Значение_если_истина ссылаемся на ячейку, содержащую значение значение CD для этого случая. При этом в строку Значение_если_ложь вводить уже ничего не надо.

Затем находим значение | X₁ - X₂ | и окончательный результат. Окончательный результат находим с помощью функции ЕСЛИ, в которой используем логическое выражение | X₁ - X₂ | ≤ CD_0,95. Если оно истинно, выводим среднее значение результатов двух лабораторий, если ложно – сообщение «Результаты взаимонеприемлемы».

Задание.

1. Выполнить расчёты в соответствии с примером 3.1.

2. Выполнить расчёты в соответствии с примером 3.2.

3. Выполнить расчёты в соответствии с примером 3.3.

4. Выполнить расчёты в соответствии с примером 3.4. Используя полученную электронную таблицу, оценить приемлемость результатов, полученных при испытаниях различных видов продукции в двух лабораториях, и в случае их приемлемости – окончательный результат. Результаты занести в табл. 3.3.

Таблица 3.3.

Продукт	Показатель	Лаборатория 1	Лаборатория 2	r	R	Окончательный результат
Х	n	Х	n
Бензин авиационный Б 95/130	Свинец, г/дм3	2,03 С		1,95 М		0,03	0,05
Бензин автомобильный АИ-93	Кислотность, мг/100 см3	0,7 С		0,6 С		0,10	0,25
Бензин автомобильный АИ-95	Октановое число	95,2 С		95,7 С		0,5	1,0
Солод ячменный	Влажность, %	4,3 С		5,1 М		0,2	0,5
Ацетон технический	Массовая доля метанола, %	0,05 М		0,04М		0,0004	0,0009

Примечание: С – результат получен как среднее значение параллельных определений, М - результат получен как медиана параллельных определений

 

ИСКЛЮЧЕНИЕ ГРУБЫХ ОШИБОК

Лабораторная работа № 4

Критерий Н.В. Смирнова

Результаты испытаний выборки могут содержать одно или несколько значений, заметно отличающихся от остальных (выбросов). После анализа причин появления выбросов, если есть основания полагать, что они случайны, оценивают при помощи того или иного критерия, являются ли эти значения грубыми ошибками (промахами). Если такая оценка показывает, что это грубые ошибки, их исключают из результатов испытаний. Надо иметь в виду, что неправомерное отбрасывание выбросов может привести к неверным выводам. Несмотря на использование критериев, оценка выбросов довольно субъективна, поэтому целесообразно проводить такую оценку по нескольким критериям, и только после анализа причин выбросов.

Существует много различных критериев, каждый из которых применим в тех или иных случаях. Иногда полезно использовать оценку по нескольким критериям. Следует отметить, что в литературе иногда встречаются различные наименования для одних и тех же критериев и различные критерии с одними и теми же названиями. Кроме того, встречаются несколько различающиеся табличные значения одного и того же критерия.

Для нормально распределенной случайной величины часто используют критерий Н.В.Смирнова (на подобном алгоритме основан также критерий Граббса).

При известной генеральной дисперсии σ² (например, когда генеральная дисперсия достаточно точно известна по текущим измерениям) используют статистику критерия t_a. Для этого строят вариационный ряд результатов испытаний (т.е. располагают их по возрастанию) и, если одно из крайних значений ряда сомнительно, вычисляют критерий для сомнительного значения х_с по формуле

(4.1)

Расчётное значение сравнивают с табличным t_a, приведённым в табл. 4.1. При tрасч > t_α результат xс считают грубой ошибкой и отбрасывают.

Пример 4.1. Проведены испытания выборки из партии бумаги на определение разрывной длины. При этом получены результаты, м: 3720, 3980, 3820, 3700, 3870, 3810, 3730, 3840, 3870, 3810. Генеральная дисперсия разрывной длины рассчитана ранее по результатам предыдущих испытаний, представленным в табл. 1.3. Оценить, при доверительной вероятности 0,9, имеется ли в полученных результатах грубая ошибка.

Возможный вариант выполнения примера 4.1 показан на рис.4.1.

Вводим в лист EXCEL результаты испытаний и доверительную вероятность, рассчитываем уровень значимости и объём испытаний (функция СЧЁТ). Затем копируем значение дисперсии, рассчитанное

Таблица 4.1.

n	ta
a=0.1	a=0.05	a=0.01
	1,50	1.74	2,22
	1.70	1,94	2.43
	1,84	2,08	2,57
	1,94	2,18	2,68
	2,02	2,27	2,76
	2,09	2,33	2,83
	2,15	2,39	2,88
	2,20	2,44	2,93
	2,24	2,48	2,97
	2,28	2,52	3,01
	2,32	2,56	3,04
	2,35	2,59	3,07
	2,38	2,62	3,10
	2,41	2,64	3,12
	2,43	2,67	3,15
	2,46	2,69	3,17
	2,48	2,71	3,19
	2,50	2,73	3,21
	2,52	2,75	3,22
	2,54	2,77	3,24
	2,56	2,78	3,26
	2,57	2,80	3,27
	2,59	2,82	3,28
	2,70	2,93	3,40
	2,79	3,02	3,48
	2,86	3,08	3,54
	3,08	3,29	3,72
	3,34	3,53	3,95
	3,53	3,70	4,11

в задании 3 лабораторной работы 1. Для этого используем команды Копировать и Специальная вставка. В диалоговом окне последней команды отмечаем указатель Значения, чтобы копировалась не формула, по которой рассчитывали дисперсию, а значение дисперсии. Результаты располагаем в вариационный ряд (по возрастанию), например, кнопкой на панели инструментов с указанием в диалоговом окне Сортировать в пределах указанного выделения. В вариационном ряду выглядит сомнительно последнее значение ряда 3980. Однако, чтобы электронную таблицу можно было использовать при вводе других данных, проверим на выброс также и нижнее значение ряда.

 

Рис.4.1. Вариант расчёта для примера 4.1.

 

Рассчитываем среднее значение ряда, при этом, чтобы таблица была пересчитываемой, в формулу СРЗНАЧ вводим диапазон примерно на 1000 значений. Далее находим t_расч для максимального и минимального значений вариационного ряда по формуле (4.1). При этом используем в расчётных формулах соответственно функции МАКС и МИН, чтобы электронная таблица была пересчитываемой. Пример формулы виден на рис. 4.1.

Для нахождения t_a вводим в электронную таблицу табличные значения t_a в пределах n от 3 до 25. Для более высоких значений n значения t_a можно c приемлемой точностью рассчитать по уравнениям, указанным в табл. 4.2.

Эти уравнения вводим в соответствующие ячейки таблицы значений критерия для строки >25, с указанием в них ссылки на значение n.

Таблица 4.2.

α	ta при n > 25
0,1	0,3053∙ Ln(n) + 1,6513
0,05	0,2849∙ Ln(n) + 1,9517
0,01	0,2648∙ Ln(n) + 2,4839

Затем находим табличное значение t_a. Для этого удобно сначала найти номер строки и столбца таблицы критерия, на пересечении которых находится нужное значение.

Для нахождения номера столбца используем функцию ЕСЛИ. В её диалоговом окне вводим логическое условие α = 0,1 (разумеется, вместо символа α надо сделать ссылку на соответствующую ячейку), а в строке Значение_если_истина вводим соответствующий номер столбца, в данном случае 1. Затем устанавливаем курсор в конец формулы в строке формул, снова вводим функцию ЕСЛИ (нажав треугольник в правом верхнем углу окна программы и выбрав Другие функции…), вводим в строки диалогового окна α = 0,05 и соответствующий номер столбца. Таким же образом вводим α = 0,01 и соответствующий ему номер столбца.

Для нахождения номера строки также в формуле дважды используем функцию ЕСЛИ. Для первой функции ЕСЛИ используем логическое условие n <= 25 и ссылку на значение n. Для второй функции ЕСЛИ используем логическое условие n > 25 и значение 26, т.е. когда n > 25, значение t_a будет находиться в строке 26 таблицы критерия по одной из формул табл. 4.2. В конце формулы для нахождения строки указываем -2, поскольку первая строка таблицы критерия соответствует n = 3, т.е. номер строки на 2 меньше значения n. В конечном счёте получим формулу для номера строки =ЕСЛИ(E6<=25;E6)+ЕСЛИ(E6>25;26)-2. В этой формуле суммируются два значения, полученных по функциям ЕСЛИ, но по одной из функций заведомо будет получен ноль, т.к. в любом случае одно из логических условий будет неверно. Таким образом, получаем номер строки либо по первой, либо по второй функции ЕСЛИ.

По найденным номерам столбца и строки находим t_a с использованием функции ИНДЕКС. На первом шаге выбираем Массив;номер_строки;номер_столбца. На втором шаге в диалоговом окне функции ИНДЕКС в качестве массива указываем диапазон значений t_a, а также ссылки на строку и столбец.

Далее определяем, являются ли крайние значения вариационного ряда грубыми ошибками, используя функцию ЕСЛИ. Например, для максимального значения в диалоговое окно вводим логическое условие tрасч > t_α, для истинности этого условия вводим строку «Гр. Ошибка», для ложности этого условия вводим строку «Не ошибка». Для ячеек, где выводятся эти сообщения, можно задать для наглядности цветной шрифт, например, красный.

В результате реализации электронной таблицы выводятся сообщения, являются ли крайние значения вариационного ряда грубыми ошибками. Однако при этом отбрасывать грубые ошибки следует по одной. Так, если максимальное значение ряда будет равно 5000 (попробуйте подставить это значение вместо 3980), оба крайних значения определятся как грубые ошибки. Но если по здравом рассуждении отбросить 5000 как грубую ошибку, то минимальное значение ряда 3700 уже не определяется как грубая ошибка.

При нормальном распределении исследуемого параметра и объёме испытаний не более 25 используют статистику критерия Н.В. Смирнова u_α (если объём испытаний больше 25, выборочное СКО достаточно близко к генеральному, и можно использовать статистику t_a).

Строят вариационный ряд результатов испытаний, и, если одно из крайних значений ряда сомнительно, вычисляют критерий для сомнительного значения х_с по формуле

Расчётное значение сравнивают с табличным u_a, приведённым в табл. 4.2.

Таблица 4.2.

n	ua
a =0.1	a =0.05	a =0.01
	1,15	1,15	1,15
	1,42	1,46	1,49
	1,60	1,67	1,75
	1,73	1,82	1,94
	1,83	1,94	2,10
	1,91	2,03	2,22
	1,98	2,11	2,32
	2,03	2,18	2,41
	2,09	2,23	2,48
	2,13	2,29	2,55
	2,17	2,33	2,61
	2,21	2,37	2,66
	2,25	2,41	2,70
	2,28	2,44	2,75
	2,31	2,48	2,78
	2,34	2,50	2,82
	2,36	2,53	2,85
	2,38	2,56	2,88
	2,41	2,58	2,91
	2,43	2,60	2,94
	2,45	2,62	2,96
	2,47	2,64	2,99
	2,49	2,66	3,01

При uрасч > u_α результат xс считают грубой ошибкой.

Пример 4.2. По результатам испытаний, приведённым в примере 4.1, оценить для различных доверительных вероятностей, имеется ли грубая ошибка, если генеральная дисперсия разрывной длины заранее неизвестна. Провести оценку также в случае, если последнее значение вариационного ряда будет не 3980, а 4010.

Для выполнения примера достаточно скопировать электронную таблицу, созданную в примере 4.1, ввести табличные значения критерия Смирнова u_a вместо табличных значений t_a, рассчитать выборочное СКО s вместо генерального σ, (подумайте, какой при этом задать диапазон) и изменить диапазон для расчёта х_ср (как изменить?). После этого можно провести оценку выбросов.

Задание.

1. Выполнить расчёты в соответствии с примером 4.1. Определить, содержат ли данные грубую ошибку при доверительных вероятностях 0,95 и 0,99.

2. Скопировать электронную таблицу примера 4.1 на другой лист и оценить, имеется ли грубая ошибка при доверительных вероятностях 0,9, 0,95 и 0,99 в ряду значений некоторого нормально распределённого параметра, полученного по результатам испытаний: 431 442 288 290 295 310 319 587 335 335 343 455 351 355 367 379 379 383 404 426 447 367 375 467 486 387 391 391 407 420. При этом генеральная дисперсия заранее неизвестна. Учитывая, что объём испытаний больше 25, модифицировать электронную таблицу так, чтобы генеральное среднеквадратическое отклонение определялось по данным испытаний, с учётом возможности пересчёта таблицы при вводе других исходных данных.

3. Выполнить расчёты в соответствии с примером 4.2.

 

Лабораторная работа № 5

Критерий Диксона

При нормальном распределении контролируемого параметра для исключения грубых ошибок распространен критерий Диксона. Коэффициент (критерий) Диксона обозначают, как показано в табл. 5.1. При наличии одновременно наименьшего и наибольшего выброса (двусторонних выбросов) считают, что односторонний выброс один.

Таблица 5.1.

Объём выборки n	Число односторонних выбросов в вариационном ряду
один	два и больше
3–7 8–10 11–13 14–30	r10 r11 r21 r22	r20 r20 r21 r22

Рассчитывают коэффициент Диксона, как показано в табл. 5.2.

Таблица 5.2.

Коэффициент Диксона для выброса
наименьшего	наибольшего
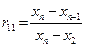
r20=	r20=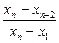

Здесь х₁, х₂, …,х_n – результаты испытаний в вариационном ряду.

Рассчитанный коэффициент Диксона r_расч сравнивают с его табличным значением r_табл, приведённым в табл. 5.3.

Выброс считается случайным и отбрасывается, если r_расч > r_табл

Пример 5.1. При испытаниях древесины сосны получены значения предела прочности при сжатии вдоль волокон в испытанных образцах, МПа: 36,0 65,0 40,0 41,5 42,5 51,0 44,0 46,5 38,0 33,0 48,0. Провести проверку на наличие грубых ошибок по критерию Диксона при доверительной вероятности 0,95, если известно, что распределение показателя соответствует нормальному.

Вариант выполнения примера 5.1 показан на рисунке 5.1.

Вводим в лист EXCEL результаты испытаний и упорядочиваем их в вариационный ряд. В вариационном ряду выглядит сомнительно наибольшее значение ряда 65,0. Поэтому создаём электронную таблицу для одного одностороннего выброса. Чтобы её можно было использовать при вводе других данных, проверим на выброс также и минимальное значение ряда. Вводим доверительную вероятность и номера значений предела прочности (от 1 до 30), рассчитываем объём испытаний (функция СЧЁТ). Для наименьшего и наибольшего значений ряда в соответствии с табл. 5.1 и табл. 5.2 рассчитываем коэффициенты Диксона r₁₀, r₁₁, r₂₁, r₂₂, используя функции НАИМЕНЬШИЙ, НАИБОЛЬШИЙ, МИН, МАКС. Например, коэффициент r₂₂ для наи-

Таблица 5.3.

n	Доверительная вероятность	Обозначение коэффициента Диксона
0.9	0.95	0.99	0.995
	0.886	0.941	0.988	0.994	r10
	0.679	0.765	0.889	0.926
	0.557	0.642	0.780	0.821
	0.482	0.560	0.698	0.740
	0.434	0.507	0.637	0.680
	0.479	0.554	0.683	0.725	r11
	0.441	0.512	0.635	0.677
	0.409	0.477	0.597	0.639
	0.935	0.967	0.992	0.996	r20
	0.782	0.845	0.929	0.950
	0.670	0.736	0.836	0.865
	0.596	0.661	0.778	0.814
	0.545	0.607	0.710	0.746
	0.505	0.565	0.667	0.700
	0.474	0.531	0.632	0.664
	0.517	0.576	0.679	0.713	r21
	0.490	0.546	0.642	0.675
	0.467	0.521	0.615	0.649
	0.492	0.546	0.641	0.674	r22
	0.472	0.525	0.616	0.647
	0.454	0.507	0.595	0.624
	0.438	0.490	0.577	0.605
	0.424	0.475	0.561	0.589
	0.412	0.462	0.547	0.575
	0.401	0.450	0.535	0.562
	0.391	0.440	0.524	0.551
	0.382	0.430	0.514	0.541
	0.374	0.421	0.505	0.532
	0.367	0.413	0.497	0.524
	0.360	0.406	0.489	0.516
	0.354	0.399	0.486	0.508
	0.348	0.393	0.475	0.501
	0.342	0.387	0.469	0.495
	0.337	0.381	0.463	0.489
	0.332	0.376	0.457	0.483

меньшего значения ряда рассчитывается по формуле

=(НАИМЕНЬШИЙ(B4:B33;3)-МИН(B4:C32))/(НАИБОЛЬШИЙ

(B4:B33;3)-МИН(B4:B33)).

Здесь x₃ рассчитывается по функции НАИМЕНЬШИЙ(B4:B33;3), т.е. с позицией 3 от минимума ряда, а x_n-2 по функции (НАИБОЛЬШИЙ(B4:B33;3) т.е. с позицией 3 от максимума ряда.

 

Рис. 5.1. Вариант расчёта для примера 5.1.

 

Далее находим r_расч, выбирая его из рассчитанных коэффициентов в зависимости от объёма испытаний n. По таблице 5.1, если n > 13, то r_расч= r₂₂, если 10 < n < 14, то r_расч= r₂₁, и т.д. Автоматический выбор r_расч для минимального значения ряда можно реализовать так: в строку формул вводим функцию ЕСЛИ, в диалоговом окне которой вводим логическое выражение Е5>13. Если это выражение истинно, то r_расч= r₂₂, поэтому в строке Значение_если_истина ссылаемся на ячейку, содержащую значение коэффициента r₂₂. Если логическое выражение Е5>13 ложно, то Е5<14. Это часть условия для r₂₁. Вторую часть условия для r₂₁, Е5>10, вводим через функцию ЕСЛИ в строке Значение_если_ложь, т.е. в эту строку вводим функцию ЕСЛИ. В открывшемся при этом новом диалоговом окне вводим логическое выражение Е5>10. Таким образом будут заданы оба условия для r₂₁, и поэтому в строку Значение_если_истина нового диалогового окна ссылаемся на ячейку, содержащую значение коэффициента r₂₁. В строке Значение_если_ложь второго диалогового окна вводим снова функцию ЕСЛИ, и в открывшемся третьем диалоговом окне вводим логического выражения для r₂₁, Е5>10. В строке Значение_если_истина ссылаемся на ячейку, содержащую значение коэффициента r₁₁. Далее для коэффициентов r₁₁ и r₁₀ поступаем так же, как при выборе значений коэффициентов r₂₁ и r₂₂. При этом для r₁₀ в строку Значение_если_ложь вводить уже ничего не надо.

Аналогично находим r_расч для максимального значения вариационного ряда. Затем вводим таблицу значений r_табл, за исключением значений коэффициента r₂₀, поскольку он не используется, когда в вариационном ряду имеется один выброс.

Из таблицы значений r_табл находим нужное значение r_табл. Для этого сначала находим нужные номера столбца и строки, подобно тому, как это сделано в примере 4.1 лабораторной работы № 4. В частности, номер строки находится по формуле =E5-2, где Е5 - адрес ячейки с объёмом испытаний, от которого отнимается 2, поскольку таблица начинается с n = 3 = 2+1. По номеру столбца и строки, используя функцию ИНДЕКС, находим нужное значение r_табл. Затем по функции ЕСЛИ, выводим сообщения, являются ли грубыми ошибками минимальное и максимальное значения вариационного ряда.

Задание.

1. Выполнить расчёты в соответствии с примером 5.1.

2. Определить, при каких доверительных вероятностях данные содержат грубые ошибки. Занести результаты в табл. 5.4.

Таблица 5.4.

Довер. вероятность	Критерий Диксона табличный	Критерий Диксона расчётный	Минимум вариационного ряда = 33	Максимум вариационного ряда = 65
Для минимума	Для максимума
0,9
0,95				Не ошибка	Гр. ошибка
0,99
0,995

 

Лабораторная работа № 6

Критерий Ирвина

Если распределение результатов испытаний не является нормальным или неизвестно, для оценки выбросов можно использовать критерий Ирвина. При этом строят вариационный ряд значений и оценивают сомнительные значения на одном или обоих краях ряда. Для этого вычисляют расчётное значение критерия Ирвина:

η_расч=(х_к-х_{к пред})/s,

где х_к – сомнительное значение, х_{к пред} – предыдущее значение в вариационном ряду.

Полученное расчётное значение критерия Ирвина сравнивают с табличным η_табл, значения которого обычно находят из соответствующей таблицы. Однако при автоматизированной обработке данных удобно рассчитывать η_табл с приемлемой точностью по зависимостям, показанным в табл. 6.1, при изменении объёма испытаний n в пределах от 3 до 1000 (при n =2 η_табл= 2,3 для Р= 0,9, η_табл= 2,8для Р= 0,95 и η_табл= 3,6 для Р= 0,99 ).

Если η_расч > η_табл, то рассматриваемое значение отбрасывают и проверяют следующее. Проверку продолжают, пока не получат η_расч < η_табл.

Таблица 6.1.

Доверительная вероятность Р	ηтабл
0,9	2 n -0,5+0,6
0,95

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: