 |
Исходные уравнения для анализа переходных процессов в синхронных машинах
|
|
|
|
Тема: «Уравнения синхронных и асинхронных машин
Для математического моделирования электромеханических переходных процессов в системах электроснабжения»
Невольниченко В.Н.
Одесса 2012
УРАВНЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ СИСТЕМ ЭЛЕКТРОСНАБЖЕНИЕ
Математические модели для расчета переходных процессов в системах электроснабжения
Математическое описание ПП в сложных ЕЕС складывается на основе уравнений для каждого ее элемента. В общем случае основными элементами ЕЕС являются: СМ, трансформаторы, линии электропередач и потребители электрической энергии, основные из которых - АД.
Полная модель ЕЕС должна учитывать как электромагнитные так и электромеханические ПП, потому СМ и АД необходимо моделировать с использованием их "полных" систем дифференциальных уравнений. При этом уравнения АД записываются в неподвижной системе координат a, b, 0, а уравнение СМ - в системе координат, вращающейся со скоростью ротора, d, q, 0. Для преобразования параметров из одной системы координат в другую используются выражения, которые приведены в [1].
Уравнения элементов электрической сети записываются в дифференциальной форме и неподвижной системе координат a, b, 0. Их преобразование позволяет получить аналитические выражения, при использовании которых удается избежать численного дифференцирования при решении таких уравнений.
При рассматривании автономных СЭП, в которых отсутствие условия постоянства частоты приводит к появлению новых переменных, система уравнений для всей ЕЕС дополняется уравнениями первого закона Кирхгофа в дифференциальной форме.
Исходные уравнения для анализа переходных процессов в синхронных машинах
|
|
|
Основными уравнениями для анализа переходных процессов в синхронной машине являются следующие дифференциальные уравнения в неподвижных координатах А, В, С
 |
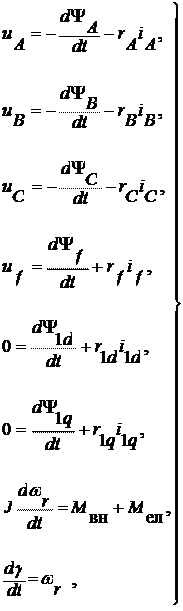(1.1)
где 
- результирующие потокосцеплення соответственно фаз статора, обмотки возбуждения, продольного и поперечного демпферных контуров;
- мгновенные значения токов соответственно фаз статора, обмотки возбуждения, продольного и поперечного демпферных контуров;
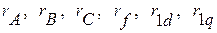- активные сопротивления соответственно фаз статора, обмотки возбуждения, продольного и поперечного демпферных контуров;
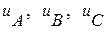- мгновенные значения напряжения фаз статора синхронной машины;
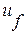- напряжение цепи возбуждения;
J -момент инерции вращающихся масс ротора;
Мел - электромагнитный момент (тормозной для генератора и вращающий для двигателя);
Мвн - внешний момент (вращающий момент турбины для генератора или тормозной момент механизма для двигателя);
w(r - угловая скорость ротора ;
γ - угол между магнитной осью фазы А и поперечной осью q ротора.
Уравнение движения записано при условиях, что положительные знаки всех моментов приняты для случая, когда они действуют в сторону ускорения ротора в положительном направлении.
Потокосцеплення, которые входят в (1.1), представляют собой линейные зависимости от тока данного контура и токов магнитносвязанних с ним других контуров. Коэффициентами пропорциональности при этом будут индуктивность L контура, который рассматривается, и его взаимоиндуктивности М с другими контурами. Введя для L и М индексы соответствующих обмоток, можно записать:
(1.2)
При вращении ротора только индуктивности Lf, L1d, L1q, Mf1d можно считать неизменными, все же другие L и M зависят от положения ротора относительно обмоток статора и, соответственно, являются функциями времени.
Положение ротора в пространстве фиксируется углом 
между магнитной осью фазы А и поперечной осью q ротора, или γ'= π/2 + γ между магнитной осью фазы А и продольной осью d ротора.
|
|
|
Синусоидальность электродвижущей силы (ЕДС) холостого хода, которая наводится в статоре, уже указывает на закон изменения взаимных индуктивностей MAf = MfА между обмоткой возбуждения и каждой фазой статора. Очевидно, что он выражается синусоидальной функцией с периодом 2p, максимум которой наступит при совпадании магнитных осей этих обмоток (
:
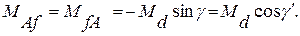(1.3)
Изменение индуктивностей фазных обмоток и взаимных индуктивностей между этими обмотками обусловлено вращением явнополюсного ротора, поскольку при этом непрерывно изменяется магнитное сопротивление потокам, которые определяют данные индуктивности.
Изменение магнитных потоков происходит с периодом p, то есть в 2 раза меньшим, так как при повороте ротора на угол p повторяется предыдущий угол изменения магнитного сопротивления. Например, индуктивность фазы А
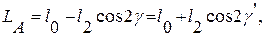(1.4)
где l 0 и l 2 - неизменная составляющая и амплитуда второй гармоники этой индуктивности.
Дальше при записи уравнений Парка - Горева будут введенные индуктивности Ld, Lq, L 0. Тогда
(1.5)
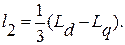(1.6)
Система дифференциальных и алгебраических уравнений (1.1) - (1.2) является нелинейной из-за того, что имеет периодически изменяющиеся коэффициенты самоиндукции и взаимоиндукции и потому не имеет аналитического решения. Принимаются меры для того, чтобы избавиться от этих переменных коэффициентов. Для этого исходные уравнения преобразуют, принимая для статора и ротора единую систему координат:
1) Жестко связанную с ротором (d, q, 0), то есть такую, которая вращается с одинаковой с ним скоростью wr. Для преобразования уравнения фаз статора А, В, С записывают в системе координат d, q, 0, вращающейся со скоростью ротора. Уравнения для контуров ротора при этом не изменяются.
2) Жестко связанную со статором - a, b, 0 (неподвижную). Уравнения для контуров ротора записывают в неподвижной двуосной системе координат. Уравнения фаз статора тоже преобразуются, поскольку их также записывают в системе координат a, b,0. Такая система координат используется для анализа переходных процессов в асинхронных машинах.
|
|
|
3)Систему координат, которая вращается с синхронной скоростью wс. Такая система координат иногда используется для анализа переходных процессов в многомашинных системах электроснабжения.
|
|
|
