 |
Система относительных единиц
|
|
|
|
Уравнения машины (4.1) и (4.2) часто записывают в относительных единицах. Переход к ним:
1) упрощает запись уравнений, освобождая их от некоторых постоянных коэффициентов;
2) облегчает вычисления, так как переменные выражаются удобными числами (долями единиц);
3) позволяют сравнивать между собой различные модификации и типы машин.
Существует несколько систем относительных единиц. Мы воспользуемся т.н. взаимной системой относительных единиц.
В ней в качестве базисных единиц принимаются:
1. Для угловой частоты: wб = wс = 2pf, при этом базисная угловая скорость ротора
,
где р – число пар полюсов машины.
2. Базисный ток – амплитуда номинального фазного тока статора, кА:
.
3. Базисное напряжение – амплитуда номинального фазного напряжения статора, кВ:
.
Остальные базисные величины для статорных переменных определяются следующими соотношениями:
4. Базисное сопротивление статора, Ом:
.
5. Базисная мощность – номинальная мощность машины (статора), МВА
,
где Uном ф и Іном ф – действующие значения номинальных фазных напряжения и тока статора.
6. Базисная индуктивность статора, Генри:
.
7. Базисное потокосцепление статора, Вебер:
.
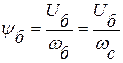8. Базисный момент, нм
.
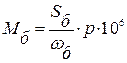9. Иногда время тоже выражают в относительных единицах. Базисное время
.
При указанных базисных единицах и синхронной угловой частоте в сети, то есть когда w = wс = const имеем
,
,
,
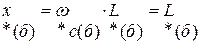то есть индуктивное сопротивление численно равно индуктивности, а потокосцепление численно равно ЭДС или падению напряжения.
Во взаимной системе относительных единиц базисные величины для роторных контуров подчиняются приведенным выше соотношениям, а базисная мощность принимается одинаковой как для статора, так и для каждого из роторных контуров.
|
|
|
Ранее мы получили выражения для синхронной ЭДС по поперечной оси Еq. Это ЭДС холостого хода, но при отсутствии насыщения.
С одной стороны:
с другой:
,
где 
- относительное значение тока возбуждения, приведенного к статору, во взаимной системе относительных единиц.
Отсюда имеем
,
.
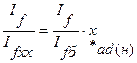10. Базисный ток обмотки возбуждения 
.
11. Базисное напряжение обмотки возбуждения 
.
12. Базисное сопротивление обмотки возбуждения 
,
тогда 
.
Однако, относительное сопротивление обмотки возбуждения удобнее определять по постоянной времени Tf0 обмотки возбуждения при всех разомкнутых контурах, с которыми она имеет магнитную связь:
Для демпферных контуров надо также находить свой базисный ток, который будет отличаться от базисного тока возбуждения, поскольку для них будет другое число витков и другой обмоточный коэффициент. Поэтому для демпферных контуров относительное сопротивление удобно определять по постоянным времени, которые находятся экспериментально или оцениваются по конструктивным размерам машины.
Запишем уравнения (1) и (2) Парка-Горева во взаимной системе относительных единиц, но выражая время и инерционную постоянную Тj в секундах. Покажем ход преобразований первых пяти уравнений системы (1) на примере первого уравнения этой системы. Разделим левую и правую часть этого уравнения на 
с учётом того, что 
или
.
Введём в это уравнение скольжение ротора машины относительно синхронной оси, вращающейся с постоянной угловой частотой wс
.
Отсюда
,
.
Введём это выражение в преобразуемое уравнение. Тогда, если не водить специальных обозначений для переменных в относительных единицах, получим для данного и других пяти уравнений
|
|
|
,
,
,
, (5.1)
,
.
Если синхронный генератор работает параллельно с системой неограниченной мощности, характеризуемой вектором напряжения 
, то
,
,
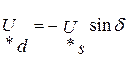здесь напряжение выражено в принятой системе относительных единиц,
d - угол между поперечной осью машины q и вектором напряжения , выраженный в радианах,
Yd и Yq включают в себя потокосцепления внешней сети до узловой точки или шин приёмной системы.
В расчётах удобно, пользуясь для выражения величин взаимной системой относительных единиц, напряжение возбуждения все же приводить в долях возбуждения холостого ходя, поскольку
,
а 
и поэтому его легко определить из векторной диаграммы установившегося режима.
Установим связь между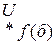 
и 
.
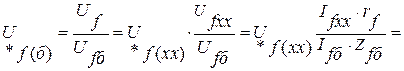
Полученное выражение для 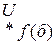подставляется в четвёртое уравнение системы (5):
. (5.2)
Для записи уравнения движения ротора в относительных единицах разделим обе его части на базисный момент
и учтём, что
,
тогда получим
,
и с учётом того, что 
, где S – скольжение, получаем
, (5.3)
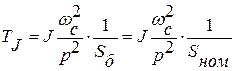, с. (5.4)
Здесь: Т j – механическая постоянная инерции ротора генератора и турбины или двигателя и приводимого во вращение механизма, J ― момент инерции ротора в т.м2, Sном ― в кВА, ωс=314,159 1/с, р ― число пар полюсов.
В системе уравнений (5.1) - (5.4) все величины заданы в относительных единицах и, следовательно, безразмерные, кроме времени и инерционной постоянной T J. Время и инерционная постоянная выражаются в секундах.
Угол d между синхронно вращающейся осью, совпадающей по направлению с вектором напряжения , и осью q ротора при интегрировании скольжения получается в радианах
.
Механическая постоянная инерции ротора может быть рассчитана также через маховый момент GD 2 = 4 J и синхронную частоту вращения n н (об/мин).
С учётом того, что
,
,
получаем
. (5.5)
Учитывая, что в относительных единицах индуктивности и индуктивные сопротивления равны, находим
,
,
, (5.6)
,
,
где xd, xq – синхронные индуктивные сопротивления обмоток статора по продольной и поперечной осям;
xad, xaq – индуктивные сопротивления взаимоиндукции (реакции статора) по продольной и поперечной осям;
xf, x1d, x1q – индуктивные сопротивления обмотки возбуждения, продольной и поперечной демпферных обмоток. Все сопротивления в (8) выражены в относительных единицах при номинальных условиях машины, все величины роторных контуров приведены к статору.
|
|
|
Если учесть, что потокосцепления воздушного зазора равны
,
, (5.7)
то можно записать
,
, (5.8)
,
,
.
По первому закону Кирхгофа имеем
,
,
,
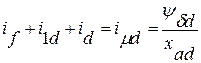получим
,
где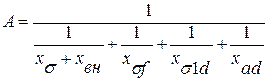 
. (5.9)
Аналогично
, (5.10)
где 
Выражения (11), (12) используются для расчёта 
и 
, а выражения (10) – для вычисления токов id, iq, if, i1d, i1q.
Для СД с массивным ротором или с массивными полюсами учитывается вытеснение тока в роторе и насыщение по путям рассеяния введением зависимостей приведенных активного сопротивления и сопротивления рассеяния эквивалентного демпферных контуров по продольной и поперечной осям от скольжения.
Методика расчёта активных и реактивных сопротивлений, входящих в уравнения Парка-Горева, приведена в методических указаниях к лабораторным работам.
|
|
|
