 |
Уравнения Парка-Горева синхронной машины
|
|
|
|
Уравнение электрического равновесия цепи статора, записанное через изображающие векторы напряжений, токов и потокосцеплений в неподвижной системе координат, имеет вид
где 
;
wс – угловая частота напряжения, которая при работе синхронного генератора параллельно с системой неограниченной мощности равна синхронной.
Это же уравнение в системе координат, вращающейся со скоростью ротора wr, получим, используя выражение для перехода изображающего вектора во вращающейся системы координат к неподвижной, которое, например, для тока имеет вид
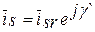
где 
- изображающий вектор тока статора в неподвижной системе координат;
- изображающий вектор тока статора во вращающейся системе координат;
- угол между магнитной осью фазы А и осью d ротора.
Получаем
,
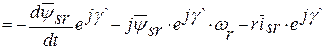т.к. 
.
В результате, в системе d, q, 0, вращающейся со скоростью ротора wr, уравнение равновесия цепи статора, записанное через изображающие векторы, имеет вид
.
Уравнения равновесия напряжений ротора
,
,
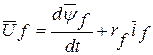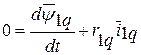
при этом остаются неизменными, так как входящие в него величины с самого начала определялись именно в системе координат ротора.
Выразим изображающие векторы через их составляющие по осям вращающейся комплексной плоскости, помня, что действительная ось комплексной плоскости направлена вдоль оси d, а мнимая ― вдоль отрицательного направления оси q. В результате получаем:
,
,
,
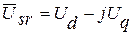Подставив эти выражения в выражение для 
, получим:
.
Приравнивая отдельно действительные и мнимые части, получим
,
,
,
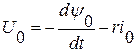, (4.1)
,
.
Эта система уравнений должна быть дополнена ещё уравнением движения или механического равновесия моментов на валу
|
|
|
,
.
Здесь Мвнешн. – вращающийся момент турбины для генератора Мт или момент механизма Ммех для двигателя;
wr – угловая скорость ротора;
- электромагнитный момент;
J – момент инерции вращающихся масс ротора, выраженный в кг×м2
Преобразование переменных статора в системе координат А, В, С в новые переменные, связанные с системой координат d, q, 0 являясь формально математическим приёмом, имеет простое физическое объяснение.
При преобразовании переменных трёхфазная обмотка статора заменяется эквивалентной двухфазной, жёстко связанной с осями d и q ротора (вращается с той же скоростью, что и ротор со скоростью wr ротора).
Дифференциальные уравнения равновесия дополним алгебраическими, связывающими потокосцепления и токи соответствующих контуров.
Принимаем допущения:
1) в продольной и поперечной осях машины, кроме потоков рассеяния существуют потоки в воздушном зазоре, пронизывающие все контуры, расположенные по соответствующим осям машины;
2) все параметры роторных контуров приведены к статору (как – уточним позднее)
Тогда выражения для потокосцеплений статорных и роторных контуров, входящих в систему (2), имеют вид
,
,
, (4.2)
,
,
.
Так как преобразованные обмотки статора d и q неподвижны относительно ротора, то индуктивности и взаимные индуктивности этих обмоток, входящие в выражения (2), постоянны, если не учитывать изменения насыщения магнитной цепи. Таким образом, преобразование переменных (переход от системы координат А, В, С к осям d и q) позволяет избавиться от периодических коэффициентов в дифференциальных уравнениях (1) синхронной машины.
Уравнения (1) и (2) выражают основу теории обобщённой электрической машины.
При постоянной частоте вращения ротора (wr = const) с учётом принятых допущений система уравнений (1) и (2) становится системой линейных дифференциальных уравнений, допускающей аналитическое решение, то есть можно получить аналитическое выражение для изменения тока статора во времени при коротком замыкании.
|
|
|
В системе (1) первые слагаемые первых двух уравнений для обмоток d и q статора представляют ЭДС трансформации, поскольку они вызываются изменением величин соответствующих потокосцеплений, а вторые слагаемые – ЭДС вращения. В установившемся режиме ЭДС трансформации отсутствуют.
В рассмотренной выше модели синхронной машины, соответствующей уравнениям Парка-Горева, ЭДС вращения представлены лишь частично, так как при синхронном вращении обмоток и магнитных потоков никаких ЭДС вращения в этих обмотках нет. Только при перемещении обмоток относительно вращающихся магнитных потоков, что в общем случае также имеет место при переходном процессе, в обмотках наводятся дополнительные ЭДС вращения (точнее ЭДС скольжения ― 
в обмотке d и 
в обмотке q, где wr ¹ wс), поток при работе СМ параллельно с системой неограниченной мощности всегда вращается с синхронной скоростью.
|
|
|
