 |
Уравнение для расчета переходных процессов в асинхронных машинах
|
|
|
|
Асинхронную машину можно представить как совокупность сложных трехмерных электрических и магнитных цепей, которые состоят из участков с разными магнитными проницаемостями. Поэтому точное описание реальной машины с помощью уравнений Максвелла оказывается практически невозможным. При исследованиях и инженерных расчетах пользуются упрощенными представлениями о физических процессах в машине, приблизительно учитывая, а в некоторых случаях и вообще не рассматривая влияние изменения насыщения магнитной цепи, эффекта вытеснения тока, потерь в стали, полигармонического состава токов и других факторов. Уравнения, которые записаны с такими предположениями, являются лишь приближенной математической моделью реальной машины. Однако во многих случаях они описывают явления в машине и ее поведение с достаточной для практических целей точностью, если только с нужной точностью определены основные параметры машины. В зависимости от особенностей явлений, которые анализируются, степень приближения может быть разной. Поэтому допущения, которые принимаются, должны быть четко обсуждены, а их приемлемость обоснована или доказана экспериментально.
Совокупность магнитно связанных электрических цепей, которые представляют собой асинхронную машину, характеризуется тем, что их коэффициенты взаимоиндукции периодически изменяются. При составлении уравнений обычно учитывают только первую гармонику индуктивностей обмоток. Для исключения периодически изменяющихся коэффициентов применяется замена реальных фазных значений токов, напряжений, потокосцеплений проекциями обобщенных векторов на оси координатной системы, наиболее удобной для исследований. При этом уравнения для статорных и роторных цепей записывают в единой системе координат ― для асинхронных машин часто в неподвижной в пространстве системе координат α, β, 0.
|
|
|
Основой математического описания модели асинхронной машины, как и любого электромеханического преобразователя энергии, являются дифференциальные уравнения электрического и механического равновесия системы, а также уравнения превращения электромагнитной энергии в механическую. В наиболее обобщенной форме в системе координат, которая вращается с произвольной скоростью k, эти уравнения имеют вид:
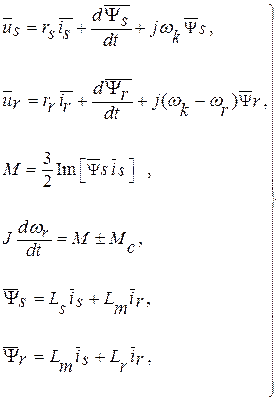
(6.1)
где 
, 
, 
- мгновенные значения обобщенных пространственных векторов токов, потокосцеплений и напряжений;
- активные сопротивления фазы статора (ротора);
- индуктивности сопротивления обмоток статора (ротора);
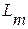- взаимная индуктивность между статорними и роторными обмотками;
- угловая скорость ротора эквивалентной двухполюсной машины;
и 
- момент инерции электромеханической системы и момент сил сопротивления, которые приведены к валу эквивалентной машины.
При выводе (6.1), кроме рассмотренных выше допущений, пренебрегают также вихревыми токами, потерями в стали и влиянием формы пазов. Переменные в (6.1) выраженны в именованных единицах, что создает определенные неудобства при обобщении результатов и исследовании многомашинных систем. Поэтому все переменные уравнений выражаются в относительных единицах:
(6.2)
При исследовании режимов асинхронных двигателей с коротко замкнутым ротором можно исключить из уравнений ток ротора 
. В этом случае система (1.89) преобразуется к виду
(6.3)
Для решения уравнений на ЭВМ векторные величины должны быть представлены в алгебраической форме. Поэтому обобщенные векторы трехфазной системы выражаются через их составляющие по действительной α и мнимой β осям неподвижной системы декартовых координат, что равносильно замене трехфазной обмотки статора эквивалентной двухфазной. Положительное направление магнитной оси α совмещают с положительным направлением магнитной оси фазы А статора, а положительное направление магнитной оси β принимают опережающим положительное направление магнитной оси α на 90º. Кроме того, каждое из уравнений необходимо разрешить относительно производной. В результате этого уравнения асинхронного двигателя представляются в форме, удобной для их решения численными методами, например Эйлера или Рунге ― Кутта.
|
|
|
(6.4)
|
|
|
