 |
Вынужденные колебания в консервативной нелинейной системе при гармоническом силовом воздействии, гармонический баланс
|
|
|
|
При воздействии гармонической силы на линейную систему в ней, как хорошо известно, возникает гармонический вынужденный процесс с частотой вынуждающей силы и с амплитудой, определяемой параметрами системы, частотой и внешней силой. В частности, при совпадении частоты воздействующей силы с частотой свободных колебаний системы (при w 1 = w 0) в ней, при отсутствии потерь (консервативная система), возбуждается бесконечно нарастающий вынужденный колебательный процесс, соответствующий наступлению резонанса. Однако, если по-прежнему рассматривать консервативную, но нелинейную систему, то вследствие возможной неизохронности при возникновении в ней колебаний условие резонанса с изменением амплитуды колебаний может измениться, и в этом случае мыслимо установление конечной амплитуды вынужденного колебания при любой частоте воздействия. К нелинейным системам неприменим метод комплексных амплитуд, поэтому анализ вынужденных колебаний в таких системах часто проводят методом гармонического баланса.
В общем случае консервативная нелинейная система второго порядка, находящаяся под силовым воздействием, описывается функцией
 . .
| (4.3) |
Будем считать, что нелинейность слабая, и в качестве основного приближения рассмотрим решение  .
.
 Рис. 29. Графическое определение амплитуды вынужденных колебаний в нелинейной системе.
Рис. 29. Графическое определение амплитуды вынужденных колебаний в нелинейной системе.
|  Рис. 30. Зависимость амплитуды вынужденных колебаний от частоты воздействия в системе с "жёсткой" нелинейной возвращающей силой.
Рис. 30. Зависимость амплитуды вынужденных колебаний от частоты воздействия в системе с "жёсткой" нелинейной возвращающей силой.
|
Подставим решение в (4.3)
 . .
| (4.4) |
Если нелинейность не слишком велика, положим f (a cos(w 1 t)) = f (a)cos(w 1 t). Так как (4.4) должно удовлетворяться при любых значениях аргументов, то необходимо потребовать, чтобы
|
|
|
 . .
| (4.5) |
Решение этого уравнения удобно получить графически (рис. 29). Строя заданную функцию z = - f (a) и прямую  , мы в точке их пересечения получим искомое решение a, т. е. найдём амплитуду приближенного гармонического решения. Для разных P и w 1, т. е. для различных амплитуд и частот воздействия, можно найти значение a и построить соответствующие кривые a (w 1) для различных P, т. е. построить некоторый аналог резонансным кривым для резонанса в линейных системах.
, мы в точке их пересечения получим искомое решение a, т. е. найдём амплитуду приближенного гармонического решения. Для разных P и w 1, т. е. для различных амплитуд и частот воздействия, можно найти значение a и построить соответствующие кривые a (w 1) для различных P, т. е. построить некоторый аналог резонансным кривым для резонанса в линейных системах.
Для f (а), имеющей характер, показанный на рис. 29, эти кривые a (w 1) имеют вид, изображенный на рис. 30, где показаны три такие кривые, соответствующие трем значениям P (P 1> P 2> P 3). При P = 0 получим кривую, изображенную штриховой линией; она соответствует собственной частоте свободных колебаний w изучаемой системы при различных амплитудах и называется скелетной кривой. Рассматривая характер полученных резонансных кривых, мы замечаем следующее: при частоте воздействия w 1, меньшей частоты свободных колебаний w 0, в системе всегда происходит однозначно определяемое колебательное движение с амплитудой, зависящей от величин P и w 1. Когда впроцессе своего изменения w 1 становится больше w 0, то, начиная со значения w 1 > w 0, в системе, кроме существовавшего ранее движения, оказываются возможными еще два колебательных процесса с различными амплитудами. При этом амплитуда исходного вынужденного процесса с ростом w 1 продолжает расти (область А), амплитуды же двух вновь появившихся решений изменяются так, что одна из них растет с ростом w 1(область С), другая уменьшается (область В). Линия раздела этих областей показана на рис. 30 штрих-пунктирной кривой, и она проходит через точки амплитудных кривых с вертикальными касательными. Таким образом, если для заданной амплитуды P воздействующей силы ее частота w 1 изменяется, начиная с малых значений до любых сколь угодно больших значений и обратно, мы получим однозначное решение, соответствующее одной из ветвей резонансной кривой в области А. Отметим, что колебания в областях А и В для одной и той же амплитуды внешней силы P отличаются друг от друга по фазе на p.
|
|
|
Если же рассматривать поведение амплитуды вынужденного движения, начиная с больших значений w 1, то мы будем двигаться по ветви резонансной кривой в области В в сторону уменьшения w 1 и роста a до той точки, где касательная к резонансной кривой станет вертикальной. Дальнейшее уменьшение w 1 может сопровождаться лишь скачком амплитуды вынужденного колебания а на ветвь кривой в области А (показано стрелкой) и дальнейшим изменением а в соответствии с формой этой части резонансной кривой. Таким образом, мы не обнаружили естественного хода процесса, при котором система оказалась бы на ветви резонансной кривой в области С. Это согласуется с тем, что строгий анализ особенностей всех трёх типов решений показывает неустойчивость движений, соответствующих области С, в отношении любых сколь угодно малых вариаций параметров.
Правда, не следует придавать слишком большого значения сделанным выводам о вынужденных колебаниях при больших а и сильных уклонениях w 1 от w 0, так как в этих условиях действительное движение может значительно отличаться от гармонического и допущения, положенные в основу построения рассмотренной картины резонансных кривых, станут несправедливыми не говоря уже о расхождениях, связанных с заменой реальной системы консервативной.
Рассмотрим теперь ту же задачу приближенным аналитическим способом, методом гармонического баланса.
Для исследуемой системы, находящейся под гармоническим воздействием, используем уравнение (4.3). Задавшись гармоническим решением
 , ,
| (4.6) |
получаем для P = 0
 , ,
| (4.7) |
где f (a cos(wt) + b sin(wt)) - периодическая функция с периодом 2 p / w. Таким образом, её можно разложить в ряд Фурье
 .
.
Оставляем только первую гармонику, тогда
 .
.
Так как выражение должно выполняться для любого момента времени, то коэффициенты при cos(wt) и sin(wt) равны нулю, т. е. w 2 a = a 1, w 2 b = b 1.
Для свободных колебаний оба уравнения совершенно идентичны, так как, ввиду произвольности выбора начала отсчёта времени, значение x может быть с равным успехом выражено через cos(wt) или sin(wt) и их комбинацию. Коэффициенты a 1 и b 1 определяются из соотношений для нахождения коэффициентов ряда Фурье
|
|
|

| (4.8) |
Отсюда частота собственных колебаний
 ,
,
где t = wt.
Для примера рассмотрим колебания в резонансном контуре. Напряжение на конденсаторе меняется по следующему закону u = q (1 + e q 2)/ C 0. Выбирая в качестве обобщённой координаты x заряд на конденсаторе, получим
 .
.
Примем начальные условия в виде b = 0, тогда
 .
.
Выражение для неизохронной частоты приобретает вид
 . .
| (4.9) |
Найденное выражение для частоты свободных колебаний несколько отличается от выражения (2.15), полученного при использовании метода последовательных приближений для контура с нелинейной ёмкостью. Однако с точностью до членов с более высокими степенями 3/4 ea 2 эти два выражения приводятся одно к другому, а различие, существенное при не слишком малых значениях ea 2, связано с тем, что в методе последовательных приближений мы используем не чисто гармоническое решение, а учитываем наличие высших (например, третьей) гармонических составляющих.
Для конденсатора с квадратичной нелинейностью, характерной для варикапа, в уравнении (4.3) следует взять
 .
.
В этом случае получится w = w 0, так как метод гармонического баланса, как и метод ММА, является приближением первого порядка.
Возвращаясь к анализируемой задаче, рассмотрим теперь случай действия внешней силы на систему, т. е. P ¹ 0. Тогда, отыскивая решение с частотой внешней силы в нашем приближении, положим

| (4.10) |
и введём обозначение w 1 t = t. Из (4.3) и (4.10) следует, что
 .
.
Разлагая функцию - f (a cos t + b sin t) в ряд Фурье, и пренебрегая по-прежнему в рамках гармонического баланса высшими гармониками фурье-разложения, получим уравнения
 ; ;  . .
| (4.11) |
Здесь, как и раньше a 1 и b 1 ищем по формулам (4.8). Используя эти соотношения, находим
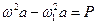  . .
| (4.12) |
Второе из этих уравнений может удовлетворяться только при b = 0, тогда из первого уравнения получаем
 .
.
Здесь w (a) - частота свободных колебаний. Если эта зависимость известна, например, из формулы (4.9), можно найти зависимость a (w 1, P) амплитуды вынужденных колебаний от частоты и амплитуды внешнего воздействия.
|
|
|
Генерация высших гармоник
Явление, когда появляются высшие гармоники при гармоническом воздействии на нелинейную систему, называется генерацией гармоник.
Рассмотрим, например, колебания в нелинейной консервативной системе с конденсатором с сегнетоэлектриком при достаточно большой амплитуде гармонического воздействия, причём собственная частота малых свободных колебаний системы близка к утроенной частоте воздействия. Для конденсатора с сегнетоэлектриком
 .
.
Уравнение (4.3) будет в этом случае иметь вид:
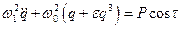 , где , где  . .
| (4.13) |
При большой нелинейности нельзя предполагать, что решение близко к гармоническому. Можно ожидать появления высших гармоник. Мы допустили, что есть третья гармоника, т. е. если w 1 - частота внешнего воздействия, то w 1» w 0/3. В этом случае можно ограничиться только первой и третьей гармониками и искать вынужденные колебания в виде
 ,
,
тогда получается
 .
.
Оставляя в разложении f (q) в ряд Фурье только члены с cos t и cos3 t и приближенно положив - f (q) = a 1cos t + a 3cos3 t, получим систему двух уравнений
 ; ;  . .
| (4.14) |
Для выбранного вида нелинейности имеем

| (4.15) |
Для свободных колебаний системы с нелинейностью (P = 0) из (4.14) получим уравнения
 ; ;  . .
| (4.16) |
Здесь w - основная частота свободных колебаний нелинейной системы, заменившая частоту w 1, которая задавалась внешним воздействием. Из последней системы можно найти соотношение между амплитудами гармоник
 .
.
Нетрудно убедиться, что из системы (4.16) можно получить частоту свободных колебаний:
 .
.
Как мы видим, w отличается от w 0 лишь на величину порядка e.
Иначе обстоит дело при наличии воздействия (P ¹ 0). Тогда частота возбуждаемого колебания будет задаваться внешним воздействием. В рассматриваемом случае частота w 0 близка к 3 w 1. В результате соотношение между амплитудами основного колебания и его третьей гармоники должно быть совсем иным.
Для определения a 1 и a 3 имеем систему (4.14). Заменяя из (4.16) в первом уравнении a 1 на w 2 a 1, получаем
 ,
,
откуда выражение для амплитуды основной гармоники
 .
.
Здесь мы учли, что w» w 0 (с точностью до величины порядка e), а w 0» 3 w 1.
 Рис. 31. Амплитуда третьей гармоники.
Рис. 31. Амплитуда третьей гармоники.
| Для определения a 3 воспользуемся вторым соотношением из (4.14), тогда, подставив его во второе уравнение системы (4.15), получим
 .
Введём относительную расстройку x: .
Введём относительную расстройку x:
 ,
тогда получим уравнение третьей степени относительно a 3: ,
тогда получим уравнение третьей степени относительно a 3:
|
 .
.
Так как e ¹ 0, то на e можно сократить
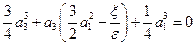 . .
| (4.17) |
Это решение описывает установившийся процесс. Таким образом, нелинейность зависит от отношения x / e. Зависимость амплитуды третьей гармоники от этого отношения представлена на рис. 31.
|
|
|
|
|
|


