Силовой расчет группы Ассура II класса 2 вида.

Определяем по диаграмме нагрузки. Вычерчиваем класс группы Ассура для исследуемого положения механизма в масштабе .

Расчет начинается с определения тангенциальной составляющей R. 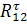из условия равновесия 2-го звена используя уравнение моментов относит точки С.

Определяем реакци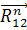и и из условия равновесия всей группы Асура, используя векторное уравнение: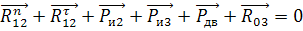

Для решения векторного уравнения построим план сил в масштабе

Определяем отрезки для построения известных сил на на плане

 

Для определения реакции в шарнире С записываем векторные уравнения равновесия каждого из звеньев в группе в отдельности:

Силовой расчет ведущего звена

Ведущее звено образует со стойкой вращательную кинематическую пару и является кривошипом. Все действующие на звено силы можно привести в общем случае к силе и моменту. Со стороны второго звена на него действует реакция R₂₁. Необходимо обеспечить заданный закон движения ведущего звена. С этой целью к ведущему звену прикладывают уравновешивающую силу (момент), которая уравновешивала все действующие внешние силы, действующие на ведущее звено и превращала бы тем самым в статически уравновешенную систему. Следовательно, уравновешивающую силу (момент) можно рассматривать как движущую, приводящую механизм в движение в соответствие с требуемым законом.

Реакция в шарнире ведущего звена зависит от того, что прикладывать к ведущему звену – уравновешивающую силу или момент.

 

Прикладываем уравновешивающую силу к ведущему звену.

 

 

 

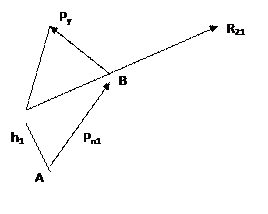
Определяем уравновешивающую силу из условия равновесия ведущего звена, используя уравнение моментов относительно т.А

Определяем реакцию R₀₁ в опоре А из условия равновесия ведущего звена, использую векторное уравнение

Для решения векторного уравнения графическим методом построим план сил в масштабе , определяем отрезки для построения известных сил на плане

Py

 

 

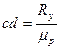
Определяем значение R₀₁ из построенного плана

Теорема Н.Е. Жуковского о жестком рычаге

Она используется для определения уравновешивающей силы (момента) на ведущем звене при заданной нагрузке.

Жёстким рычагом называется материализованный план скоростей, принимаемый за абсолютно твёрдое тело с неподвижной точкой в полюсе.

Теорема:

Сумма моментов всех сил, действующих на механизм, включая инерционные силы и уравновешивающую, перенесённых параллельно самим себе в одноимённые точки плана скоростей повёрнутого на 90 градусов относительно полюса этого плана равна нулю.

Доказательство:

Пусть к звеньям механизма приложены внешние силы, инерционные и уравновешивающая. Из кинематического анализа можно определить скорости приложения этих сил и углы между направлениями сил и скоростей.

Из принципа возможных перемещений известно, что для равновесия системы необходимо, чтобы сумма элементарных работ всех действующих сил на возможном перемещении была бы равна нулю.

- элементарная работа

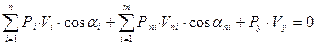
Приложим силу к концу вектора скорости повёрнутого на 90 градусов на плане скоростей

,

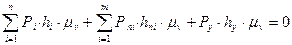
Таким образом, доказано, что если повернуть на 90 градусов план скоростей, приложив в соответствующих точках внешние, инерционные и уравновешивающую силы, то этот план скоростей можно рассматривать как жёсткий рычаг, находящийся в равновесии под действием этих сил.

Задачи сопромата. Основные понятия и определения. Гипотезы и допущения

 

Сопротивление материала – это наука, дающая основы для расчётов на прочность, жёсткость и устойчивость.

Прочность – это способность выдерживать внешнюю нагрузку, не разрушаясь.

Жёсткость – это способность сопротивляться изменению первоначальной формы и размера.

Устойчивость – это способность сохранять первоначальную форму равновесия.

 

Основная задача сопромата – это создание работоспособной, прочной, долговечной и в тоже время экономичной конструкции.

Основные понятия и определения:

Сопромат внешних активных сил принято называть нагрузкой. Нагрузки классифицируется:

1) По способу приложения:

1.1 объёмные

1.2 поверхностные

1.2.1 распределённые

а) по площади

б) по линии

1.2.2 сосредоточенные

а) сила

б) момент

2) По характеру взаимодействия

2.1 статические - изменяется от 0 до конечно значения

2.2 динамические – мгновенно приложенный удар повторно-переменный.

Все эти виды нагрузок вызывают деформацию. Основные виды деформации сложные, однако их можно представить состоящими из небольшого числа основных:

1. Растяжение (сжатие)

2. Сдвиг (срез)

3. Кручение

4. Изгиб

Элементы конструкции, которые воспринимают деформацию имеют как правило сложную форму, но их можно представить в виде простых составных элементов, для которых выполняются расчёты сопромата.

Брус – это элемент конструкции, у которого длина намного больше поперечных размеров. Бывают прямолинейные и криволинейные. Линия, проходящая через центр масс поперечного сечения бруса, называется осевой. Груз с прямой осью называют стержнем. Основные характеристик бруса: длина и размер поперечного сечения.

Оболочка – элемент конструкции, ограниченный параллельными поверхностями, расположенными на близком расстоянии. Плоские оболочки называю плитами и пластинами.

Массивное тело – элемент конструкции, у которого высота, длин и ширина одного порядка.

Основные гипотезы и допущения:

1. Гипотеза о сплошном строении материала. Материал полностью заполняет объём тела и пустоты в нём отсутствуют.

2.

3. Гипотеза об однородности материала. Частицы материала обладают одинаковыми свойствами, которые не зависят от размеров тела.

4. Гипотеза об изотропности материала. Свойство материала в любых направлениях одинаково (древесина – анизотропный)

5. Гипотеза плоских сечений. Поперечное сечение остаётся плоским и нормальным к оси до и после приложения нагрузки.

Допущения: 1) деформация на столько меньше размеров тел, что не оказывает влияния на расположение тел 2) допущение о линейной зависимости между деформацией и нагрузкой.

Считается, что деформация прямо пропорциональна нагрузкам их вызывающим.

 

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: