 |
Тема 3. Показатели вариации
|
|
|
|
ПРАКТИКУМ
ПО ТЕОРИИ СТАТИСТИКИ
Курск 2005
Курский государственный университет
В.И.Гуров, Г.Н.Яценко
Практикум по теории статистики
Рекомендован
учебно-методическим советом факультета экономики и менеджмента
Курского государственного университета
в качестве учебного пособия для студентов экономических специальностей
Курск 2005
ББК 60.6Я 73
Гуров В.И., Яценко Г.Н. Практикум по теории статистики. – Курск: Курск. гос. ун-т, 2005. – 136 с.
В «Практикуме по теории статистики» содержатся решения типовых задач и задачи для самостоятельного решения по важнейшим темам: «Сводка и группировка статистических данных», «Средние величины», «Показатели вариации», «Выборочное наблюдение», «Ряды динамики», «Индексы», «Корреляционный анализ». Их решение поможет в усвоении учебного материала.
Издание предназначено для студентов экономических факультетов, позволит усвоить курс теории статистики.
Рецензент: А.С. Паранян – д-р экон. наук. профессор, зав. кафедрой анализа и
аудита Курской государственной сельскохозяйственной академии
имени проф. И.И.Иванова
© Гуров В.И., Яценко Г.Н., 2005
© Курский госуниверситет, 2005
Содержание
Введение. 5
Тема 1. Сводка и группировка статистических данных. 6
Тема 2. Средние величины. 16
Тема 3. Показатели вариации. 27
Тема 4. Выборочное наблюдение. 44
Тема 5. Ряды динамики. 53
Тема 6. Индексы.. 83
Тема 7. Статистические методы изучения взаимосвязей социально-экономических явлений. 97
7.1. Виды и формы связей. Понятие о статистической связи. 97
7.2. Основные статистические методы изучения взаимосвязей. 99
|
|
|
7.3. Корреляционно-регрессионный метод анализа. Уравнение регрессии как форма аналитического выражения статистической связи. 104
7.4. Однофакторные (парные) модели регрессии. 106
7.5. Показатели тесноты связи альтернативных признаков. 118
Приложение 1. 129
Приложение 2. 130
Приложение 3. 131
Приложение 4. 131
Приложение5. 132
Приложение 6. 133
Приложение 7. 134
Приложение 8. 135
Введение
В современных условиях предъявляются повышенные требования к уровню подготовки экономистов любой специальности.
Работа экономиста постоянно связана с использованием и анализом статистических данных, которые необходимы для оценки состояния социально-экономических процессов любой сферы деятельности на всех уровнях хозяйствования и управления.
Чтобы всесторонне анализировать происходящие в стране процессы, необходимо овладеть статистической методологией и, прежде всего, основами теории статистики – науки, разрабатывающей понятия и категории статистики, методы отбора, обработки, обобщения и анализа массовых общественных явлений, структурных различий, методы изучения динамики и анализа закономерностей развития, моделирования и прогнозирования конкретных социально-экономических процессов.
Знание статистики значительно повышает профессиональный уровень экономиста, его компетентность и, следовательно, качество аналитической работы.
Усвоение курса общей теории статистики невозможно без самостоятельного решения задач по расчету статистических показателей, составлению таблиц, графиков и т.д. Практикум по теории статистики поможет студентам в практических самостоятельных занятиях и при выполнении письменных контрольных заданий, курсовых работ.
«Практикум» состоит из семи тем, соответствующих темам курса теории статистики. В каждой теме приводится разбор одной или нескольких типовых задач, а также предлагаются задачи для самостоятельного решения. Приведенные в задачах данные – условные.
|
|
|
Тема 1. Сводка и группировка статистических данных
Практические занятия по теме предусматривают решение следующих типов задач:
1. Построение рядов распределения по количественному признаку.
2. Построение группировки.
3. Проведение вторичной группировки.
Решение типовых задач
№1. Для двадцати рабочих зарегистрированы следующие индивидуальные значения (варианты) изучаемого признака – тарифные разряды:
| Табельный номер рабочего | ||||||||||||||||||||
| Тарифный разряд рабочего (X) | 
|
Построить ряд распределения рабочих по тарифному разряду.
Решение: Тарифный разряд – дискретный признак. Располагая значения признака первичного ряда в возрастающем порядке, получаем ранжированный ряд:
| Табельный номер рабочего | ||||||||||||||||||||
| Тарифный разряд рабочего (X) |
Рассматривая этот ранжированный ряд, видим, что некоторые значения признака повторяются. Цифры, показывающие количество повторений отдельных вариант, называются численностями (частотами) и обозначаются буквой f. Сумма частот (
) равна объему изучаемой совокупности (n).
Таблица 1.1
Ряд распределения рабочих по тарифному разряду
| Тарифный разряд (Х) | Число рабочих с данным тарифным разрядом | ||
| В абсолютном выражении (f) | В долях к итогу ( )
| В процентах к итогу
( )
| |
| А | |||
| 0,25 |
Продолжение таблицы 1.1
| А | |||
| 0,35 0,25 0,15 | |||
| Итого: | 1,0 |
Оформляя результаты подсчета численностей (частот) в таблицу 1.1, получаем дискретный вариационный ряд, характеризующий распределение изучаемого признака.
|
|
|
Основными элементами вариационного ряда являются варианты (х) и соответствующие им частоты (f).
Частоты ряда, выраженные в относительных числах (долях) и рассчитанные путем деления каждой частоты на их общую сумму, называются частостями и обозначаются W. Их можно определять и в процентах.
№2. Имеются данные о стаже работы на предприятии по 15 рабочим одной бригады. Первичный ряд величины стажа работы на данном предприятии отдельных рабочих выглядит следующим образом (в годах):
2,2; 1,4; 8,4; 2,4; 4,3; 11,4; 3,2; 4,8; 7,1; 6,2; 5,3; 5,8; 4,4; 5,6; 3,8.
Построить ряд распределения рабочих по стажу работы.
Решение: Стаж работы – непрерывно варьирующий признак. Определяем величину интервала группировочного признака:
,
где - Xmin и Xmax наименьшее и наибольшее значения признака в совокупности.
Количество групп (интервалов) в ряду при достаточном числе наблюдений (n>200-300) рекомендуется брать от 10 до 20; при предполагаемом нормальном распределении часто берут количество групп равным 12. По способу Стерджесса размер интервала устанавливается в зависимости от величины размаха вариации и численности единиц в изучаемой совокупности (n) по формуле:
.
В нашем примере количество групп примерно равно 5 (точнее 4,907)
.
Существуют следующие правила записи величины интервала группировки. Если величина интервала (i) имеет:
- один знак до запятой, например 0,77; 2,571; 3,82, то число округляется до десятых 0,8; 2,6; 3,8;
- две значащие цифры до запятой, например, 16, 891, то величина интервала округляется до целого числа (до 16);
- трехзначное, четырехзначное и так далее число, то эту величину следует округлять до ближайшего числа кратного 100 или 50. Например, 657 следует округлять до 700, 420 – до 450 и т.д.
Нижнюю границу первого интервала принимают равной минимальному значению признака, верхняя граница первого интервала соответствует значению (
).
Для последующих групп границы определяются аналогично, т.е. последовательно прибавляется величина интервала.
Следовательно, в нашем примере интервалы рабочих по стажу работы будут следующими:
|
|
|
1,4 – 3,4; 3,4 – 5,4; 5,4 – 7,4; 7,4 – 9,4; 9,4 – 11,4.
Подсчитаем теперь число рабочих в каждой группе. Единицы с величиной признака, равной нижней границе интервала, в группу включаются, а равные верхней границе - не включаются, за исключением последнего интервала. Результаты представим в таблице 1.2, которую дополним частостями и накопленными частотами.
Накопленные частоты (F) показывают, сколько единиц совокупности имеют значение признака не больше данного значения. Определяются последовательным прибавлением к частоте в первом интервале последующих частот ряда.
Таблица 1.2
Ряд распределения рабочих по стажу работы
| Группы рабочих по стажу, г. | Число рабочих, чел., f | Число рабочих, в % к итогу, W% | Накопленные частоты, F |
| 1.4 – 3,4 3,4 – 5,4 5,4 – 7,4 7,4 – 9,4 9,4 – 11,4 | 26,7 33,4 26,7 6,6 6.6 | ||
| Итого | 100,0 |
№3. В отчетном периоде работа 30-ти предприятий отрасли характеризуется данными, представленными в табл.1.3.
Таблица 1.3
| № п/п | Основные производственные фонды, млн. руб. | Фактический выпуск продукции, млн. руб. | № п/п | Основные производственные фонды, млн. руб. | Фактический выпуск продукции, млн. руб. |
| A | A | ||||
| 1,2 2,4 3,5 4,9 3,8 6,5 1,6 2,0 4,7 | 3,7 2,9 5,6 5,4 2,8 9,8 1,8 2,5 4,5 | 3,3 3,1 7,1 3,1 3,5 3,1 5,6 2,9 2,9 | 1,3 3,4 9,0 2,5 4,6 3,6 8,2 3,9 3,9 |
Продолжение таблицы 1.3
| A | A | ||||
| 1,7 3,2 7,2 2,0 2,5 3,9 5,3 | 2,3 3,2 8,6 1,5 3,2 4,3 5,4 | 3,5 4,8 1,6 1,8 4,2 | 4,5 6,1 1,9 2,2 5,6 | ||
| 106,9 | 129,2 |
С целью выявления зависимости между стоимостью основных производственных фондов и выпуском продукции проделайте следующую работу:
1) произведите аналитическую группировку предприятий по размеру основных производственных фондов, образовав четыре группы с равными интервалами. По каждой группе предприятий подсчитайте: 1) число предприятий; 2) стоимость основных производственных фондов – всего и в среднем на одно предприятие; 3) стоимость выпуска продукции – всего и в среднем на одно предприятие. Результаты оформите в таблице. Сделайте краткие выводы;
2) произведите комбинационную группировку по двум признакам: по стоимости основных производственных фондов и выпуску продукции. Результаты оформите в виде комбинационной и корреляционной таблиц. Сделайте краткие выводы.
Решение: 1. Группировки, которые применяются для исследования взаимосвязи между явлениями, называются аналитическими. Чтобы исследовать взаимосвязь между признаками с помощью метода аналитических группировок, необходимо произвести группировку единиц совокупности по факторному признаку и по каждой группе исчислить среднее значение результативного признака, вариация которого от группы к группе под влиянием группировочного признака будет указывать на наличие или отсутствие взаимосвязи.
|
|
|
Для этого необходимо, прежде всего, определить, какой признак является факторным и какой результативным. Из экономической теории известно, что факторным признаком является среднегодовая стоимость основных фондов, а зависящим результативным признаком будет служить объем выпуска продукции. Следовательно, группировочным признаком будет служить среднегодовая стоимость основных производственных фондов. Для образования групп предприятий по стоимости основных производственных фондов определим величину интервала группировки по формуле:
млн. руб.
Определим группы: 1,2 – 2,7; 2,7 – 4,2; 4,2 – 5,7; 5,7 – 7,2.
Для подсчета числа предприятий в каждой из образованных групп, определения объемов варьирующих признаков в пределах созданных групп построим рабочую таблицу 1.4.
Таблица 1.4
Распределение предприятий по среднегодовой стоимости основных фондов
| Группы п/п | Группы предприятий по стоимости основных производственных фондов, млн. руб. | Номер и число предприятий | Основные производственные фонды, млн. руб. | Выпуск продукции, млн. руб. |
| A | Б | |||
| I | 1,2- 2,7 | 1,2 2,4 1,6 2,0 1,7 2,0 2,5 1,6 1,8 | 3,7 2,9 1,8 2,5 2,3 1,5 3,2 1,9 2,2 | |
| Итого | 16,8 | 22,0 | ||
| II | 2,7 – 4,2 | 2,8 3,2 3,9 3,3 3,1 3,1 3,5 3,1 2,9 2,9 3,5 | 2,8 3,2 4,3 1,3 3,4 2,5 4,6 3,6 3,9 3,9 4,5 | |
| Итого | 35,3 | 38,0 | ||
| III | 4,2 – 5,7 | 4,5 4,9 4,7 5,3 5,6 4,8 4,2 | 5,6 5,4 4,5 6,4 8,2 6,1 5,6 | |
| Итого | 34,0 | 41,8 | ||
| IV | 5,7 – 7,2 | 6,5 7,2 7,1 | 9,8 8,6 9,0 | |
| Итого | 20,8 | 27,4 | ||
| Всего | 106,9 | 129,2 |
Полученные в рабочей таблице показатели по группам занесем в соответствующие строки и графы сводной групповой таблицы 1.5.
Таблица 1.5
Зависимость выпуска продукции от среднегодовой стоимости основных производственных фондов
| Группы п/п | Группы предприятий по стоимости основных производственных фондов, млн. руб. | Число предпри-ятий | Стоимость основных производственных фондов, млн. руб. | Выпуск продукции, млн. руб. | ||
| Всего | В среднем на одно предприятие | Всего | В среднем на одно предприятие | |||
| А | Б | |||||
| I II III IV | 1,2 – 2,7 2,7 – 4,2 4,2 – 5,7 5,7 – 7,2 | 16,8 35,3 34,0 20,8 | 1,86 3,21 4,85 6,93 | 22,0 38,9 41,8 27,4 | 2,44 3,45 5,97 9,13 | |
| Итого | 106,9 | 3,56 | 129,2 | 4,31 |
Данные группировки показывают, что наиболее крупные предприятия имеют лучшие производственные показатели. Сравнение основных производственных фондов по стоимости и среднему выпуску продукции на одно предприятие (гр.3 и 5 табл. 1.5) по группам показывает, что с ростом стоимости основных производственных фондов увеличивается выпуск продукции в среднем на одно предприятие. Следовательно, между данными признаками существует прямая корреляционная зависимость.
II. Чтобы произвести группировку предприятий по двум признакам, необходимо каждую из образованных групп по размеру стоимости основных производственных фондов разбить на подгруппы по выпуску продукции и дать их характеристику. Представим полученные показатели в комбинационной таблице 1.6.
Таблица 1.6
Группировка предприятий по стоимости основных производственных
фондов и выпуску продукции
| Группы п/п | Группы предприятий | Число пред-приятий | Основные производственные фонды, млн. руб. | Выпуск продукции, млн. руб. | ||||
| По стоимости основных производственных фондов, млн. руб. | По выпуску продукции, млн. руб. | |||||||
| Всего | В среднем на одно предприятие | Всего | В среднем на одно предприятие | |||||
| A | Б | В | ||||||
| I | 1.2 – 2,7 | 1,3 – 3,0 3,0 – 5,0 Свыше 5,0 | - | 13,1 3,7 - | 1,87 1,85 - | 15,1 6,9 - | 2,15 3,45 - | |
| Итого | 16,8 | 1,86 | 22,0 | 2,44 | ||||
| II | 2,7 – 4,2 | 1,3 – 3,0 3,0 – 5,0 Свыше 5,0 | - | 9,2 26,1 - | 3,06 3,26 - | 6,6 31,4 - | 2.2 3,92 - | |
| Итого | 35,3 | 3,20 | 38,0 | 3,45 |
Продолжение таблицы 1.6
| A | Б | В | |||||
| III | 4,2 – 5,7 | 1,3 – 3,0 3,0 – 5,0 Свыше 5,0 | - | - 4,7 29,3 | - 4,7 4,9 | - 4,5 37,3 | - 4,5 6,21 |
| Итого | 34,0 | 4,85 | 41,8 | 5,97 | |||
| IV | 5.7 – 7,2 | 1,3 – 3,0 3,0 – 5,0 Свыше 5,0 | - - | - - 20,8 | - - 6,93 | - - 27,4 | - - 9,13 |
| Итого по подгруппам | 1,3 – 3,0 3,0 – 5,0 Свыше 5,0 | 22,3 34,5 50.1 | 2,23 3,13 5,57 | 21,7 42,8 64,7 | 2,17 3,89 7,18 | ||
| Всего | 106,9 | 3,56 | 129,2 | 6,31 |
Данные комбинационной таблицы показывают, что выпуск продукции находится в прямой зависимости от стоимости основных производственных фондов. Эту зависимость можно выявить также с помощью корреляционной таблицы 1.7.
Корреляционная таблица – это специальная комбинационная таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результативному. Концентрация частот около диагоналей матрицы данных свидетельствует о наличии и направлении корреляционной связи между признаками.
Таблица 1.7
Распределение предприятий по стоимости основных
производственных фондов и выпуску продукции
| Стоимость основных производственных фондов, млн. руб. | Выпуск продукции, млн. руб. | |||||
| 1,3- -3,0 | 3,0- -4,7 | 4,7- -6,4 | 6,4- -8,1 | 8,1- -9,8 | Итого | |
| А | ||||||
| 1,2 – 2,7 2,7 – 4,2 4,2 – 5,7 5,7 – 7,2 | - - | - | - - - | - - - | - - | |
| Итого |
Как видно из таблицы 1.7, распределение числа предприятий произошло вдоль диагонали, проведенной из левого верхнего угла в правый нижний угол таблицы, т.е. увеличение признака «стоимость основных производственных фондов» сопровождается увеличением признака «выпуск продукции». Характер концентрации частот по этой диагонали корреляционной таблицы свидетельствует о наличии прямой тесной корреляционной связи между изучаемыми признаками.
№ 4. Имеются данные о группировке предприятий по стоимости основных производственных фондов по двум отраслям промышленности, представленные в таблице 1.8
Для сравнения структуры предприятий по стоимости основных производственных фондов произведите перегруппировку предприятий первой отрасли, взяв за основу распределение предприятий второй отрасли. Сведите полученные данные в таблицу и сделайте выводы.
Таблица 1.8
| I отрасль | II отрасль | ||
| Группы предприятий по стоимости основных производственных фондов, млн. руб. | Уд. вес предприятий, % | Группы предприятий по стоимости основных производственных фондов, млн. руб. | Уд. вес предприятий, % |
| До 10 10 – 12 12 – 15 15 – 20 20 - 30 | До 10 10 – 15 15 – 25 25 – 30 Свыше 30 | ||
| Итого: | Итого |
Решение: В первой отрасли надо произвести вторичную группировку, образовав такое же число групп и с теми же интервалами, что и во второй отрасли, для чего произведем следующие расчеты и построим таблицу 1.9.
Таблица 1.9
Вторичная группировка предприятий двух отраслей по среднегодовой стоимости основных средств
| Группы предприятий по стоимости основных производственных фондов, млн. руб. | Удельный вес предприятий, % | |
| I отрасль | II отрасль | |
| До 10 10 – 15 15 – 25 25 – 30 Свыше 30 | 10+20 = 30 30 + 11* = 41 | |
= 11.
В результате перегруппировки получены сопоставимые данные по двум отраслям, которые позволяют сделать вывод о том, что во II отрасли больше предприятий, технически оснащенных (с большим объемом среднегодовой стоимости), чем в I отрасли. Удельный вес предприятий со среднегодовой стоимостью основных фондов, большей 25 млн. руб., во II отрасли 35%, а в I отрасли 19%.
Задачи
№1.1 Имеются следующие данные о месячной заработной плате рабочих бригады (тыс. руб.):
3,5; 4,0; 4,5; 5,0; 6,0; 1,5; 3,0; 3,5; 4,0; 3,0; 4,5; 4,0; 3,0; 6,5; 5,5; 7,5; 6,5; 7,0.
Постройте ряд распределения рабочих по размеру заработной платы, образовав четыре группы с равными интервалами. Постройте график ряда распределения.
№1.2 Имеются данные о дневной выручке денег от продажи товаров в торговых киосках города, тыс. руб.:
44; 46; 48; 55; 54; 58; 60; 50; 49; 55; 51.
Постройте ряд распределения торговых киосков по объему дневной выручки, образовав четыре группы с равными интервалами. Изобразите ряд графически с помощью гистограммы и полигона частот.
№1.3 Имеются данные о выработке продукции рабочими бригады за смену, шт.:
7, 8, 8, 9, 10, 12, 3, 6, 7, 8, 6, 9, 8, 6, 13, 11, 9, 11, 15, 13, 14.
Постройте ряд распределения рабочих по выработке продукции с равными интервалами. Изобразите ряд графически. Сделайте выводы.
№1.4 Имеются следующие данные о стаже рабочих бригады:
2; 4; 5; 5; 6; 7; 7; 8; 8; 10; 11; 4; 3; 3; 4; 4; 5; 9; 3;6.
1. Постройте ряд распределения рабочих по стажу работы с равными интервалами, образовав три группы рабочих.
2. Определите средний стаж рабочих бригады по данным ряда распределения и по первичным данным. Какая средняя точнее?
3. Представьте ряд распределения графически.
№1.5 Имеются следующие данные о количестве произведенной продукции рабочими цеха за смену (в штуках):
10; 14; 22; 12; 15; 11; 16; 14; 19; 23; 13; 18; 17; 16; 19; 19; 15; 25; 21; 22; 16.
1. Построить ряд распределения рабочих по количеству произведенной продукции, образовав три группы с равными интервалами.
2. По данным ряда распределения определите среднюю выработку продукции (количество произведенной продукции) на одного рабочего.
№1.6 За отчетный год имеются следующие данные по предприятиям отрасли промышленности:
| № п/п | Производство продукции, тыс.т. | Общая сумма затрат на производство продукции, тыс. руб. | № п/п | Производство продукции, тыс.т. | Общая сумма затрат на производство продукции, тыс. руб. |
| A | A | ||||
| 11,2 9,6 1,7 2,1 5,1 4,6 3,1 6,1 7,4 5,5 2,0 4,2 | 9,8 11,5 12,0 3,6 2,6 5,9 7,8 9,5 4,8 9,0 7,9 7,0 3,7 |
Для выявления связи между размером выпуска продукции и себестоимостью единицы продукции произведите группировку предприятий по объему производства продукции, образовав пять групп предприятий с равными интервалами.
По каждой группе и в целом по всем предприятиям подсчитайте:
1) число предприятий;
2) объем выпущенной продукции – всего и в среднем на одно предприятие;
3) сумму затрат – всего и в среднем на единицу продукции.
Результаты представьте в таблице. Укажите подлежащее, сказуемое и вид таблицы. Дайте анализ показателей таблицы, сделайте выводы.
№1.7 Имеются следующие данные о распределении предприятий по стоимости произведенной продукции:
| Группы предприятий по стоимости произведенной продукции, млн. руб. | Число предприятий |
| 1 – 3 3 – 5 5 – 10 10 – 30 30 - 50 |
Произведите вторичную группировку предприятий по стоимости произведенной продукции, образовав следующие группы: 1 – 5; 5 - 10; 10 – 20; 20 – 30; 30-40; свыше 40.
№ 1.8 Разработайте и постройте макет статистической таблицы, в которой была бы отражена зависимость потребления населением отдельных товаров от формирующих его факторов.
№1.9 Постройте макет таблицы, укажите подлежащее, сказуемое и вид таблицы: 1) для изучения распределения предприятий по размеру выпуска продукции; 2) для характеристики распределения работающих по размеру заработной платы; 3) для характеристики распределения предприятий по проценту выполнения плана; 4) для характеристики распределения населения по возрасту.
№ 1.10 Для изучения распределения предприятий по мощности постройте макет таблицы, в подлежащем которой должны быть группы предприятий по размеру основных фондов, а в сказуемом – число предприятий и их удельный вес в процентах к итогу, размер основных фондов, выпуск продукции – всего и на один рубль основных фондов, размер прибыли. Укажите вид таблицы.
№ 1.11 Для изучения степени механизации труда спроектируйте макет таблицы, в подлежащем которой должны быть группы предприятий по проценту механизации труда, а в сказуемом – число предприятий и их удельный вес в процентах к итогу; число рабочих, размер валовой продукции – всего и в среднем на одного рабочего. Укажите вид таблицы.
№ 1.12 Имеются следующие данные о стаже работы и средней месячной заработной плате рабочих – сдельщиков:
| № рабочего | Стаж, лет | Месячная зарплата, руб. | № рабочего | Стаж, лет | Месячная зарплата, руб. |
| 1,0 6,5 9,2 4,5 6,0 2,5 2,7 16,0 14,0 11,0 | 12,0 10,5 9,0 5,0 10,2 5,0 5,4 7,5 8,0 8.5 |
Для выявления зависимости между стажем работы и месячной заработной платой сгруппируйте рабочих-сдельщиков по стажу, образовав, пять групп рабочих с равными интервалами.
По каждой группе и в целом по совокупности рабочих подсчитайте: 1) число рабочих; 2) средний стаж работы; 3) среднемесячную заработную плату.
Результаты представьте в таблице. Дайте анализ показателей таблицы и сделайте краткие выводы.
Тема 2. Средние величины
Практические занятия предусматривают решение следующих типов задач:
1) исчисление средней арифметической простой по индивидуальным данным;
2) исчисление средней арифметической взвешенной в дискретном ряде распределения;
3) исчисление средней арифметической взвешенной в интервальном ряде распределения с закрытыми и открытыми интервалами;
4) расчет средней арифметической из групповых средних;
5) расчет средней гармонической;
6) расчет моды;
7) расчет медианы.
Решение типовых задач
№1. Имеются следующие данные о производстве рабочими продукции А за смену:
| Номер рабочего | ||||||||||
| Выпущено изделий за смену, шт. |
Определить среднюю выработку продукции рабочими данной группы.
Решение:
В данном случае расчет следует производить по формуле простой средней арифметической:
.
Простая средняя арифметическая применяется, когда данные первичны, т.е. данные не сгруппированы, представлены индивидуально в виде их перечня в любом порядке или ранжированного ряда.
№2 Имеются данные о заработной плате работников:
| Месячная заработная плата (х), тыс. руб. | Число рабочих, f | Xf |
| 5,5 6,5 8,0 9,5 11,0 | ||
| Итого: |
Определить среднюю заработную плату работников.
Решение: Основой расчета является экономическое содержание показателя:
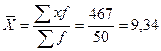тыс. руб.
Частотами (весами) могут быть относительные величины, взятые в процентах или коэффициентах. Метод расчета средней и конечный результат от этого не изменяется.
Представим данные о численности рабочих в условии приведенной выше типовой задачи в относительных величинах:
| Месячная заработная плата (х), тыс. руб. | Число рабочих в % к итогу
| Доля рабочих в коэффициентах
|
|
| 5,5 6,5 8,0 9,5 11,0 | 0,04 0.08 0,16 0,40 0,32 | 2,20 5.20 12,80 38,00 35,20 | |
| Итого: | 100,0 | 1,00 | 93,40 |
Средняя заработная плата рабочего, взвешенная по процентным соотношениям, будет равна средней, полученной при решении типовой задачи 2:
;
тыс. руб.
Если весами являются частоты, выраженные в коэффициентах, то вычисления упрощаются; так как сумма коэффициентов всегда равна единице, то расчет средней сводится к определению суммы произведений вариант на частоты (в данном случае коэффициенты):
.
тыс. руб.
№3 Имеются следующие данные:
| Группы рабочих по количеству произведенной продукции за смену, шт. | Число рабочих, f | Середина интервала, х | xf |
| 6 – 10 10 – 14 14 – 18 18 – 22 22 - 26 | |||
| Итого: | 100,0 |
Определите среднюю выработку продукции одним рабочим за смену.
Решение: исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной:
.
Чтобы применить эту формулу необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так, для первой группы дискретная величина Х
.
Дальнейший расчет производится обычным методом определения средней арифметической взвешенной:
шт.
Итак, все рабочие произвели 1500 шт. изделий за смену, а каждый в среднем произвел 15 шт.
В данном ряду варианты осредняемого признака представлены в виде закрытых интервалов. Преобразуем рассмотренный ряд в ряд с открытыми интервалами.
| Группы рабочих по количеству произведенной продукции за смену, шт. | Число рабочих, f |
| до 10 10 – 14 14 – 18 18 – 22 свыше 20 | |
| Итого: |
В таких рядах условно величина интервала первой группы принимается равной величине интервала последующей, а величина интервала последней группы – величине интервала предыдущей. Дальнейший расчет аналогичен изложенному выше.
№4. Выработка продукции за смену на предприятии характеризуется следующими данными:
| Бригада, № | Дневная выработка продукции, шт.(x) | Число рабочих, чел. (f) |
| I II III |
Определить среднедневную выработку продукции рабочих цеха.
Решение: Основой расчета является экономическое содержание показателя:
Расчет производим по средней арифметической взвешенной:
В этой задаче варианты (дневная выработка продукции) являются не индивидуальными, а средними по бригаде величинами. Весами выступает число рабочих в бригаде.
- объем произведенной продукции на предприятии.
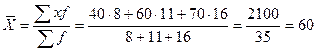шт.
№5 Определить средний процент выполнения плана прибыли акционерным обществом (АО)
| Предприятия АО | Плановая прибыль за 1 год, млн. руб. (f) | Выполнение плана прибыли, %. (х) |
| Итого: |
Требуется определить средний процент выполнения плана прибыли АО.
Решение: Основой расчета является экономическое содержание показателя:
В этой задаче варианты (процент выполнения плана прибыли) являются не индивидуальными, а средними по предприятию. Веса представлены плановой прибылью. При вычислении среднего процента выполнения плана прибыли следует использовать формулу средней взвешенной арифметической величины:
,
где - фактическая прибыль, получаемая путем умножения вариант (процент выполнения плана прибыли) на веса (плановая прибыль).
или 93,68%.
Произведя вычисления, варианты (х) лучше брать в коэффициентах. Это позволяет получить фактический объем прибыли в абсолютных значениях (млн. руб.) как в целом, так и по каждому предприятию АО, что дает возможность сравнивать фактическую прибыль с плановой, находить абсолютные приросты прибыли, производить сравнения.
Наряду со средней арифметической в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, она может быть простой и взвешенной.
№ 6. Издержки производства и себестоимость единицы продукции А по трем акционерным обществам (АО) х
|
|
|
