 |
Однофакторные (парные) модели регрессии
|
|
|
|
Парная регрессия характеризует связь между двумя признаками: результативным и факторным.
Процесс построения модели парной регрессии включает следующие основные этапы:
1) выбор формы связи;
2) определение параметров уравнения связи и проверка адекватности регрессионной модели;
3) измерение тесноты связи и проверка значимости (надежности) показателей тесноты связи.
Выбор формы связи имеет решающее значение в корреляционно-регрессионном анализе. Все дальнейшие самые тщательные расчеты могут быть обесценены, если форма связи избрана неверно.
При выборе формы уравнения регрессии качественный анализ играет важную роль для раскрытия механизма формирования корреляционной связи. Пусть, например, измеряется связь между сроком сева и урожайностью. Чрезмерно ранний и чрезмерно поздний сев ведут к снижению урожайности, максимум которой достигается при севе в оптимальные сроки. Таким образом, с ростом факторного признака (срок сева) урожайность растет, а затем снижается. Зависимость такого рода может быть выражена, например, уравнением параболы.
При всей важности теоретического анализа следует, однако, учитывать, что социально-экономические явления очень сложны. Как правило, мы не имеем о них исчерпывающей информации, а внутренняя логика их связей мало изучена. Факторы, влияющие на то или иное явление, взаимно переплетаются и взаимодействуют друг с другом. Поэтому очень часто не удается сделать теоретически обоснованный вывод уравнения регрессии, т.е. формы связи, внутренне присущей изучаемому явлению. В ряде случаев на основе теоретического анализа могут быть высказаны лишь более или менее обоснованные предположения о том, что следует ожидать линейную или какую-либо нелинейную (криволинейную) связь, имеет ли ожидаемая криволинейная функция экстремальные значения и т.п. Так, в рассмотренном примере можно утверждать, что линия регрессии – некоторая кривая, имеющая оптимум, но это отнюдь не обязательно парабола. Более того, если явление мало изучено, иногда могут быть выдвинуты и различные гипотезы о механизме и форме взаимосвязи.
|
|
|
Для проверки этих предположений и гипотез может быть использован графический метод – построение графика групповых средних, полученных в процессе аналитической группировки. Ломаная линия, изображающая изменение групповых средних результативного признака (
 ) в зависимости от изменения группировочного фактора, называется эмпирической линией регрессии (эмпирической регрессией).
) в зависимости от изменения группировочного фактора, называется эмпирической линией регрессии (эмпирической регрессией).
Наглядное представление о форме линии регрессии может дать график эмпирической линии регрессии (рис. 7.2).
На график корреляционное поле (рис. 7.1.) наносятся результаты аналитической группировки (табл. 7.4) Абсциссами этих точек являются средние значения факторного признака ( ), а ординатами – средние значения результативного признака (
), а ординатами – средние значения результативного признака ( ).
).
Если эмпирическая линия по своему виду приближается к прямой линии, это свидетельствует о наличии прямолинейной корреляционной связи между признаками. Если же эмпирическая линия связи будет приближаться к кривой (параболе, гиперболе, показательной кривой), то это дает основание считать, что в данном случае имеется
 |
криволинейная корреляционная связь, чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг эмпирической линии регрессии.
В нашем примере можно предположить, что имеется прямая, прямолинейная сильная корреляционная зависимость между объемом собственных средств и привлеченными средствами.
Форма эмпирической линии регрессии дает возможность проверить, соответствует ли фактическое соотношение признаков тому или иному теоретически предполагаемому их соотношению. При этом нужно, однако, иметь, в виду, что при относительно небольшом числе единиц совокупности (числе наблюдения) форма эмпирической линии регрессии может изменяться при изменении число групп и их границ. Поэтому при небольшом числе наблюдений нельзя слишком полагаться на форму эмпирической линии регрессии, графический метод в таких случаях может оказаться недостаточно надежным.
|
|
|
Существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи – гиперболическая.
Если факторный признак увеличивается в арифметической прогрессии, а результативный – значительно быстрее, то используется параболическая или степенная регрессия.
Если относительно формы связи могут быть выдвинуты разные теоретические гипотезы, а по виду эмпирической регрессии трудно судить о том, какой из этих гипотез наиболее соответствуют фактические данные, то в этих случаях строятся и решаются уравнения регрессии с различными формами связи, а затем с помощью специальных статистико-математических критериев оценивается их адекватность и выбирается та форма связи, которая обеспечивает наилучшую аппроксимацию (приближение) и достаточную статистическую достоверность и надежность.
Определение параметров уравнения связи и их значимости.
Аналитическая связь между факторным и результативным признаками описываются уравнениями:
прямой -  ;
;
гиперболы -  ;
;
параболы -  и т.д.
и т.д.
Выбрав тем или иным путем форму связи и построив уравнение регрессии в общем виде, необходимо далее найти числовые значения его параметров.
Оценка параметров уравнения осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.
Сущность метода наименьших квадратов заключается в нахождении параметров модели (а0, ,а1), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
|
|
|
 .
.
Для прямолинейной зависимости:
 .
.
Рассматривая f в качестве функции а0, и а1 и проводя математические преобразования (дифференцирование), получаем:
 ;
;
 .
.
Откуда система нормальных уравнений для нахождения параметров линейной полной регрессии имеет следующий вид:
 .
.
Решение этой системы в общем виде дает следующие значения параметров:


Иногда их удобно исчислить по следующим формулам, дающим тот же результат:
 где
где 


или
 ;
;  .
.
Определив значения а0, и а1 и подставив их в уравнение  , находим значения
, находим значения  , зависящие только от заданного значения х.
, зависящие только от заданного значения х.
Корреляционное уравнение по форме похоже на уравнение функциональной зависимости, но по существу отличается тем, что оно справедливо лишь для совокупности, а не для отдельных явлений и зависит от объема совокупности (чем она больше, тем параметры уравнения типичнее).
В уравнении прямой параметр 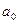 экономического смысла не имеет. Параметр
экономического смысла не имеет. Параметр  является коэффициентом регрессии и показывает изменение результативного признака при изменении факторного признака на единицу.
является коэффициентом регрессии и показывает изменение результативного признака при изменении факторного признака на единицу.
Широкое применение линейных уравнений объясняется в значительной мере тем, что зачастую значения признака х в изучаемой совокупности варьируют в весьма узких пределах. Если кривизна линии регрессии невелика, то в этих пределах отрезок кривой может быть достаточно точно описан уравнением прямой.
Кроме того, многие нелинейные функции (степенная, показательная, гипербола, парабола второго порядка) путем логарифмирования или замены переменных преобразуют в линейную форму.
Решения типовых задач
№1. Имеются выборочные данные по 15 коммерческим банкам региона:
| № п/п | х | у | № п/п | х | у | № п/п | х | у |
Построить однофакторную регрессионную линейную модель.
Решение: Предположим, что между объемом собственных средств и привлеченных средств существует линейная корреляционная связь, которую можно выразить уравнением прямой вида  .
.
|
|
|
Для определения параметров 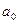 и
и  методом наименьших квадратов воспользуемся формулами
методом наименьших квадратов воспользуемся формулами  ,
,  .
.
Таблица 7.7
Расчетные значения, необходимые для исчисления 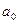 ,
,  ,
,  ,
, 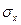 ,
, 
| Исходные данные | Расчетные значения | ||||
| № банка | Объем собственных средств, млн. руб. | Объем привлеченных средств, млн. руб. | 
| 
| 
|
| -32,6 -27,6 -19,6 -9,6 -6,6 -5,6 -4,6 1,4 4,4 9,4 9,4 12,4 17,4 24,4 27,4 | -127 -93 -77 -73 -55 -29 | 1062,76 761,76 384,16 92,16 43,56 31,36 21,16 1,96 19,36 88,36 88,36 153,76 302,76 595,96 750,76 | |||

| 
| 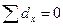
| 
| 
|
Продолжение таблицы 7.7
| Расчетные значения | |||||

| 
| 
| 
| 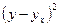
| 
|
| 4140,2 2566,8 1509,2 700,8 363,0 162,4 179,4 18,2 52,8 573,4 479,4 508,4 1531,2 2220,4 3726,4 | -32 -27 -5 -19 -7 -12 -13 | 0,23 0,29 0,07 0,30 0,22 0,03 0,14 0,03 0,04 0,09 0,05 0,05 0,05 0,05 0,06 | |||
| 18732,0 | 1,70 |

 .
.
Пользуясь расчетными значениями (см. Табл. 7.7.), подсчитаем параметры для данного уравнения регрессии:
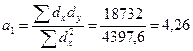 ,
,
 .
.
Следовательно, регрессионная модель объема привлеченных средств по собственным средствам банков для данного примера может быть записана в виде следующего уравнения регрессии:
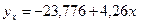 .
.
Это уравнение характеризует зависимость среднего объема привлеченных средств банков от собственных средств. Расчетные значения  , найденные по данному уравнению, приведены в таблице 7.7, гр. 9.
, найденные по данному уравнению, приведены в таблице 7.7, гр. 9.
Если параметры регрессионного уравнения подсчитаны верно, то должно соблюдаться равенство сумм теоретических и эмпирических значений объема привлеченных средств,  , а сумма разностей между эмпирическими и теоретическими значениями объема привлеченных средств должна быть равна 0
, а сумма разностей между эмпирическими и теоретическими значениями объема привлеченных средств должна быть равна 0  (гр.10. табл. 7.7).
(гр.10. табл. 7.7).
В нашем уравнении регрессии параметр  показывает, что с увеличением объема собственных средств одного банка на 1 млн. руб. объем привлеченных средств возрастает в среднем на 4,26 млн. руб.
показывает, что с увеличением объема собственных средств одного банка на 1 млн. руб. объем привлеченных средств возрастает в среднем на 4,26 млн. руб.
Если исследуемые признаки имеют разные единицы измерения, для оценки влияния факторного признака на результативный применяется коэффициент эластичности.
Коэффициент эластичности рассчитывается для каждой точки по формуле:
 ,
,
где  - первая производная уравнения регрессии.
- первая производная уравнения регрессии.
Он показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1%.
Средний коэффициент эластичности определяется для уравнения прямой по формуле:
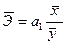 .
.
Если зависимость величин результативного признака у от значений факторного признака х имеет форму гиперболической зависимости, то есть характеризуется корреляционным уравнением  , то для определения параметров
, то для определения параметров 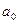 и
и  методом наименьших квадратов находим две частные производные от функции
методом наименьших квадратов находим две частные производные от функции  , по
, по 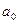 и
и  , приравниваем их к нулю, получаем систему нормальных уравнений:
, приравниваем их к нулю, получаем систему нормальных уравнений:
|
|
|
 .
.
Производим замену переменных  , получаем следующую систему нормальных уравнений:
, получаем следующую систему нормальных уравнений:
 .
.
Параметры уравнения гиперболы можно вычислить по формулам:


Гиперболическая форма корреляционной связи используется при изучении зависимости уровня себестоимости единицы продукции от объема выпуска продукции.
Если зависимость величин результативного признака у от значений факторного признака х характеризуется корреляционным уравнением параболы второй степени 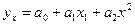 , то это параболическая зависимость.
, то это параболическая зависимость.
И парабола, и прямая являются частным случаем полинома n-ой степени вида 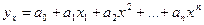 .
.
Систему уравнений для определения параметров  можно найти, приравнивая нулю частные производные от
можно найти, приравнивая нулю частные производные от  по
по  . Решив систему, определяем параметры корреляционного уравнения.
. Решив систему, определяем параметры корреляционного уравнения.
|
|
|


