Главная | Обратная связь | Поможем написать вашу работу!

Тема 4. Выборочное наблюдение

Практические занятия по данной теме предусматривают решение следующих типов задач:

1. Определение ошибки выборочной средней и доли при случайном, механическом, типическом и серийном отборах.

2. Определение необходимой численности выборки при изучении средней и доли для случайного, механического, типического и серийного отборов.

Решение типовых задач

№1. Для изучения расхода сырья на единицу продукции проведена двухпроцентная случайная выборка, в результате которой получены следующие обобщенные данные:

Расход сырья на единицу, г.	Обследовано изделий, шт. (f)
18 – 20 20 – 22 22 – 24 24 – 26 26 и выше

Определить:

1) средний расход сырья на одно изделие;

2) дисперсию и среднее квадратическое отклонений;

3) коэффициент вариации;

4) с вероятностью 0,954: предельную ошибку выборочной средней и возможные пределы расхода сырья для всей партии изделий;

5) возможные пределы удельного веса изделий с расходом сырья от 20 до 24 г.

Решение:

Все необходимые расчеты представим в таблице 4.1.

Таблица 4.1.

Расход сырья на ед.г.	Число изделий, шт.,	Середина интервала, (Х)
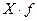
А
18-20 20 – 22 22 – 24 24 – 26 Свыше 26			-3,6 -1,6 0,4 2,4 4,4	12,96 2,56 0,16 5,76 19,36	64,8 71,68 8,32 69,12 58,08
Итого					272,0

Средний расход сырья на одно изделие в выборке равен:

г.

Вычислим дисперсию и среднее квадратическое отклонение.

Среднее квадратическое отклонение равно корню квадратному из дисперсии

Коэффициент вариации:

Предельная ошибка выборочной средней:

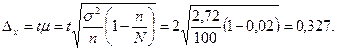
Следовательно, границы генеральной средней будут находиться в пределах

или

С вероятностью 0,954 можно утверждать, что расход сырья на единицу продукции всей партии может изменяться от 22,273 до 22,927 г.

Ошибка выборочной доли определяется по формуле:

Сначала определим выборочную долю (частость):

или 80 %

Выборка показала, что расход сырья от 20 до 24 граммов на единицу продукции приходится на 80% изделий. Определим предельную ошибку доли:

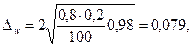или 7.9 %

С учетом ошибки генеральная доля ожидается в границах:

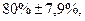или

Следовательно, с вероятностью 0,954 можно утверждать, что во всей партии продукции удельный вес изделий с расходом сырья от 20 до 24 граммов ожидается в пределах не менее 72,1 % и не более 87,9 %.

На практике применяют не только случайный отбор или механический, но и другие виды. Особое значение придается типической выборке, т.е. такой, когда генеральная совокупность разбивается на группы по изучаемому признаку, а затем из каждой группы производится отбор единиц, как правило пропорционально объему единиц в группах. Типическая выборка обеспечивает наибольшую репрезентативность.

Для типической выборки предельная ошибка репрезентативности определяется по формуле ,

где - средняя дисперсия из групповых дисперсий.

№2. По материалам выборочного обследования 625 семей области получены следующие данные:

Таблица 4.2

Семья	Обследовано семей,	Доля расходов на платные услуги, %	Доля расходов на платные услуги, в коэффициентах	Дисперсия доли,

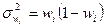
Городских поселений Сельской местности		37,0 24,0	0,37 0,24	0,2331 0,1824
	n=625	-	-	-

Выборка 2%-ная проведена по методу типического пропорционального отбора. В группах применялся механических отбор семей.

С вероятностью 0,954 определить пределы доли расходов на платные услуги жителями области.

Решение:

Доля расходов на платные услуги жителями области находится в пределах:

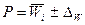Следовательно, для решения необходимо предварительно определить среднюю долю расходов по 2 группам населения, а затем ее ошибку.

Средняя доля равна:

или 34,4 %.

Для расчета ошибки выборки типического отбора надо вычислить среднюю из групповых дисперсий. В графе 5 таблицы 4.2 показан расчет групповых дисперсий доли. Вычислим среднюю из них:

Теперь вычислим предельную ошибку типической выборки:

, 3,7%;

или

Таким образом, можно с вероятностью 0,954 утверждать, что доля расходов населения области на платные услуги ожидается в пределах не менее 30,7 % и не более 38,1 %.

Аналогично вычисляется ошибка типической выборки для выборочной средней (для варьирующего признака).

№3. В механическом цехе завода в десяти бригадах работает 100 рабочих. В целях изучения квалификации рабочих была произведена 20% - ная серийная бесповторная выборка, в которую вошли 2 бригады. Получено следующее распределение обследованных рабочих по разрядам:

Рабочие	Разряды рабочих в бригаде 1	Разряды рабочих в бригаде 2	Рабочие	Разряды рабочих в бригаде 1	Разряды рабочих в бригаде 2

Необходимо определить с вероятностью 0,997 пределы, в которых находится средний разряд рабочих механического цеха.

Решение.

Определим выборочные средние по бригадам и общую среднюю:

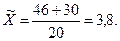
Определим межсерийную дисперсию:

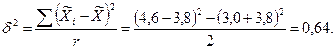
Рассчитаем среднюю ошибку выборки:

где R-число серий в генеральной совокупности;

r-число отобранных серий.

Вычислим предельную ошибку выборки с вероятностью 0,997

С вероятностью 0,997 можно утверждать, что средний разряд рабочих механического цеха находится в пределах , .

№4. 200 ящиков деталей упакованы по 40 штук в каждом. Для проверки качества деталей был проведен сплошной контроль деталей в 20 ящиках (выборка бесповторная). В результате контроля установлено, что доля бракованных деталей составляет 15 %. Межсерийная дисперсия равна 49. С вероятностью 0,997 определить пределы, в которых находится доля бракованной продукции в партии ящиков.

Решение:

Определим среднюю ошибку выборки для доли:

Предельная ошибка выборки для доли с вероятностью 0,997 равна:

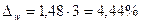
С вероятностью 0,997 можно утверждать, что доля бракованных деталей в партии может изменяться от 10,56 до 19,44 %.

Задачи

4.1 В результате случайного выборочного обследования 100 торговых киосков города получены следующие сводные данные о дневной выручке частного бизнеса:

Выручка от продажи товара, тыс. руб.	Число торговых киосков
До 100 100 – 120 120 – 140 140 – 160 160 – 180 180 – 200 200 и выше

Определить:

1) среднедневную выручку от продаж товаров;

2) среднее квадратическое отклонение и коэффициент вариации;

3) с вероятностью 0,954 ожидаемую выручку от продажи товаров частных торговых киосков города.

№4.2 Для изучения качества продукции из партии деталей в 1000 штук отобрано в механическом порядке 100 деталей. Средний диаметр обследованных деталей оказался равным 300 мм., а среднее квадратическое отклонение – 10 мм. Определите с вероятностью 0,997 пределы, в которых ожидается средний диаметр деталей во всей партии.

№ 4.3 На электроламповом заводе в порядке случайной выборки проверено 1600 ламп, из которых 48 оказались бракованными. Средняя продолжительность горения ламп равнялась 900 часам при среднеквадратическом отклонении, равном 50 часам.

С вероятностью 0,954 определите:

1) пределы, в которых находится процент бракованных ламп;

2) пределы, в которых находится средняя продолжительность горения ламп.

№4.4 В цехе 1000 человек. С целью определения затрат времени рабочими на изготовление одной детали необходимо провести выборочное обследование рабочих методом механического отбора. Предварительным обследованием установлено, что среднее квадратическое отклонение затрат рабочего времени на изготовление одной детали составило 5 мин.

Определите, какое число рабочих необходимо отобрать, чтобы с вероятностью 0,954 ошибка выборки не превышала 1 минуты.

№4.5 В городе 40 000 семей методом случайного бесповторного отбора было обследовано 3000 семей. В результате обследования было установлено, что 1000 семей являются владельцами акций.

С вероятностью 0,997 определите пределы, в которых будет находитЬся доля семей, имеющих акции в городе.

№4.6 В целях изучения норм расходования сырья на единицу продукции проведена 2–процентная механическая выборка партии изделий, в результате чего получены следующие данные:

Все изделия, г.	Число изделий, шт.
До 200 200 – 205 205 – 210 210 – 215 свыше 215
Итого

По данным обследования определите:

1) средний вес изделия: дисперсию и среднее квадратическое отклонение; коэффициент вариации;

2) с вероятностью 0,954 возможные пределы: а) среднего веса изделия во всей партии изделий; б) удельного веса изделий с расходом сырья на единицу продукции от 205 до 210 г.

№ 4.7 Из партии 4000 деталей отобрано 1000 деталей. Среди отобранных деталей 2% оказались бракованными. С какой вероятностью можно утверждать, что вся партия содержит не более 2,5 % брака.

№4.8 Из партии готовой продукции методом случайного отбора отобрано 250 изделий, из которых 5 оказались бракованными.

Определите с вероятностью 0,954 возможные пределы процента брака во всей партии.

№4.9 Средний вес изделия в выборочной совокупности, состоящей из 100 единиц, оказался 5 кг. при среднем квадратическом отклонении 0,5 кг. С какой вероятностью можно утверждать, что вес изделия во всей партии не превысит 5,1 кг.

№4.10 Сколько деталей нужно отобрать из 1000 штук для определения одного из ее параметров, чтобы с вероятностью 0,954 можно было бы утверждать, что ошибка выборки не превысит 1,0 мм. Среднее квадратическое отклонение признака-6 мм.

№4.11 Сколько деталей надо отобрать из 10000 штук для определения ее веса, чтобы с вероятностью 0,96 можно было утверждать, что ошибка выборки не превысит 0,5 г. По пробным испытаниям дисперсия веса детали установлена - 4.

№ 4.12 Для изучения трудовой деятельности лиц пенсионного возраста в районе проведена 2%-ная типичная выборка с механическим отбором в каждой группе. В результате обследования получены следующие сводные данные:

Социальные группы	Обследовано пенсионеров, чел.	Доля работающих пенсионеров (%)
Рабочие Служащие

С вероятностью 0,954 определите границы (пределы), в которых находится доля работающих пенсионеров в районе.

№4.13 Для изучения производительности труда рабочих проведено 10-ти процентное выборочное обследование по методу типического пропорционального отбора, в результате которого получены следующие данные:

Группы рабочих по разряду	Число отобранных рабочих	Среднее время обработки одного изделия	Среднее квадратическое отклонение, мин.
II IV

Определите с вероятностью 0,954, в каких пределах находится среднее время обработки одного изделия рабочими завода данных разрядов.

№ 4.14 Для установления среднего срока службы деталей из совокупности, включающей 1000 штук кассет с деталями, методом механического отбора проверено 10 штук кассет. Результаты проверки показали, что средний срок службы деталей в отобранных кассетах составил (месяцев): 7; 8,2; 8,6; 7,8; 5,8; 8,8; 7,2; 6,1; 6,0. Средний срок службы деталей в выборке – 7,6 месяца.

С вероятностью 0,997 определите пределы, в которых находится средний срок службы деталей во всей совокупности.

№4.15 Из механического цеха завода на склад готовой продукции поступило 500 ящиков деталей по 50 штук в каждом. Для установления доли бракованных деталей методом механического отбора было проверено 10 ящиков. Результаты проверки показали, что доля бракованных деталей составляет 10 %. Дисперсия серийной выборки равна 25.

С вероятностью 0,954 определите долю бракованных деталей по всей партии деталей, поступивших на склад готовой продукции.

№4.16 В механическом цехе завода А имеется 10 бригад по 20 рабочих в каждой бригаде. Для установления квалификации рабочих цеха проектируется серийная выборка.

Какое количество бригад необходимо отобрать, чтобы с вероятностью 0,954 ошибка выборки не превышала 1,0, если на основе предыдущих обследований известно, что дисперсия серийной выборки равна 0,9?

№ 4.17 Для изучения стажа работников акционерного общества проведена 1%ая механическая выборка, результаты которой предоставлены ниже:

Стаж, лет	Выборочная численность работников, человек
До 3 3 – 5 5 – 7 7 – 9 Свыше 9

Определите с вероятностью 0,954:

1) предельную ошибку выборочной средней;

2) возможные пределы, в которых находится средний стаж работников АО.

№4.18 Для установления среднего размера кредита было проведено выборочное обследование (выборка типическая, 5%-ная, с пропорциональным отбором внутри типических групп).

В результате выборки получены следующие данные:

Типы банков	Число банков	Средний размер кредита, млн. руб.	Среднее квадратическое отклонение, млн. руб.
I I I

С вероятностью 0,954 определите средний размер кредита в генеральной совокупности.

№ 4.19 Для определения среднего размера вклада в сбербанке было проведено выборочное исследование (выборка 10%-ная механическая). В результате выборки установлено, что средний размер вклада составил 3 тыс. руб. при среднем квадратическом отклонении 2 тыс. руб.

С вероятностью 0,954 определите границы, в которых будет находится средний размер вклада в сбербанке.

№4.20 В сберегательных банках города методом случайной повторной выборки было отобрано 1400 счетов вкладчиков. Средний размер остатков вклада по этим счетам составил 3,8 тыс. руб. при коэффициенте вариации 32 %.

Какова вероятность того, что ошибка репрезентативности при определении среднего размера остатков вклада не превысит 0,05 тыс. руб.?

№4.21 Сколько фирм необходимо проверить налоговой инспекции района, чтобы ошибка доли фирм, несвоевременно уплачивающих налоги, не превысила 5 %? По данным предыдущей проверки доля таких фирм составила 32 %. Доверительную вероятность принять равной: а) 0,954; б) 0,997.

№4.22 Для определения среднего размера кредита в коммерческом банке проведена 2-процентная пропорциональная типическая выборка счетов с механически отбором в группах заемщиков. В результате обследования получены следующие данные:

Заемщики	Число счетов	Средний размер кредита, тыс. руб.	Среднее квадратическое отклонение, тыс. руб.
Юридические лица Физические лица

Определите с вероятностью 0,997 возможные границы среднего размера кредита банка.

№4.23 Для характеристики уровня жизни населения района, проведена 5%-ная пропорциональная типическая выборка с механическим отбором семей. В результате которой получены следующие показатели:

Население	Обследовано, человек	Удельный вес населения с доходами ниже прожиточного минимума, %
Городских поселений Сельской местности

С вероятностью 0,954 определите границы, в которых находится доля населения с доходами ниже прожиточного минимума по району.

Тема 5. Ряды динамики

Практические занятия по данной теме предусматривают решение следующих типов задач:

1. Приведение рядов динамики к сопоставимому виду.

2. Определение среднего уровня ряда динамики.

3. Определение показателей изменения уровней ряда динамики.

4. Определение в рядах динамики общей тенденции развития.

5. Определение в рядах внутригодовой динамики индексов сезонности.

Решение типовых задач

№1. Имеются следующие данные о валовом сборе овощей в районе, тыс. ц.

Годы
В старых границах В новых границах	832,0 -			-	-	-

Приведите ряды динамики к сопоставимому виду (сомкните ряд). Укажите вид полученного ряда динамики. Изобразите его графически.

Решение:

Для приведения ряда динамики к сопоставимому виду определим для 2001 года коэффициент соотношения уровней двух рядов:

1260: 900= 1,4.

Умножая на этот коэффициент уровни динамики в старых границах, получаем их сопоставимыми с уровнями в новых границах.

В 1999 г…………………………….

В 2000 г……………………………..

Теперь представим полученные данные о валовом сборе овощей в виде ряда динамики:


1164,8	1209,6

Получим полный интервальный ряд динамики, который графически можно изобразить в виде столбиковой (рис 5.1.) или линейной диаграммы (статистическая кривая, рис. 5.2).

Рис.5.1 Валовой сбор овощей в 1999 – 2004 годах, тыс. ц.

Столбиковая диаграмма для графического изображения уровней ряда динамики удобна тем, что расстояние столбиков (прямоугольников) друг от друга не зависит от величины интервалов времени.

Рис. 5.2. Динамика валового сбора овощей в 1999 – 2004 годах (тыс. ц.)

Чаще всего для наглядного изображения динамики применяют линейные графики, особенно когда речь идет о наглядном изображении данных, характеризующих итоги какого-либо процесса за определенные периоды времени. Преимущество линейных графиков состоит в том, что динамика изображается в виде сплошной линии, характеризующей непрерывность процесса. Следует иметь в виду, что для графического изображения каких-либо явлений, данные которых охватывают различные периоды времени, интервалы между периодами времени (длина отрезков) при нанесении шкалы на оси абсцисс должны быть пропорциональны величинам продолжительности периодов.

При построении графиков большое значение имеет выбор соотношения между размерами оси абсцисс (горизонтальной оси) и ординат (вертикальной оси). При этом следует руководствоваться так называемым правилом «золотого сечения». По этому правилу чертеж должен быть расположен в прямоугольнике, в котором длина вертикальной оси (высота графика) должна относиться к длине всей горизонтальной оси (т.е. к ширине графика) приблизительно как 5:8.

Например, если общая длина горизонтальной оси равна 16 см., то общая длина вертикальной оси должна составить см.

Принято считать, что наиболее оптимальным для зрительного восприятия является график, выполненный на поле прямоугольной формы с соотношением сторон от 1:1.3 до 1:1,5. Иногда используется и поле графика с равными сторонами, т.е. имеющее форму квадрата.

При анализе рядов динамики широко применяется графический метод. Это объясняется тем, что табличное представление ряда динамики и описательные характеристики чаще всего не позволяют понять характер процесса, а по графику можно сделать определенные выводы, которые потом могут быть проверены с помощью расчетов. Графический анализ обычно задает направление дальнейшего анализа ряда динамики. В EXCEL для анализа рядов динамики (временных рядов) можно использовать средство Мастер диаграмм.

№2. Имеются данные о различной реализации хлебобулочных изделий в торговой сети города по кварталам, т:

I	II	II	IV

Приведите уровни ряда к сопоставимому виду.

Решение:

Для приведения этого ряда динамики к сопоставимому виду определим размер среднедневной реализации с учетом числа дней торговли по кварталам, т:

I	II	II	IV
4680:90=52	3640:91=40	2760:92=30	4048:92=44

Получен ряд динамики сопоставимых уровней различной реализации хлебобулочных изделий в торговой сети города по кварталам (среднедневная реализация), т:

I	II	II	IV

№3. Динамика продукции (в сопоставимых ценах) характеризуется следующими данными по АО (тыс. руб.):

Определить среднегодовое производство продукции за период 2000-2004 годы.

Решение:

Для интервального ряда динамики средний уровень исчисляется по формуле простой средней арифметической:

тыс. руб. т.е. в течение периода с 2000 по 2004 годы АО в среднем ежегодно производило продукции на 11015 тыс. руб.

№4. Имеются данные об остатках сырья и материалов на складе предприятия (тыс. руб.):

На 1.1	На 1.2	На 1.3	На 1.4
200,0	227,5	232,5	230,0

Требуется определить среднемесячный остаток сырья и материалов на складе предприятий за 1-й квартал.

Решение:

Для полного моментного ряда динамики средний уровень исчисляется по формуле простой средней хронологической:

тыс. руб.

№5. Имеются данные о товарных запасах розничного торгового предприятия (тыс. руб.):

На 1.1. 2004 г.	На 1.5. 2004 г.	На 1.8. 2004 г.	На 1.1. 2005 г.
61,1	57,5	51,3	74,7

Требуется исчислить среднегодовой товарный запас розничного торгового предприятия за 2004 год.

Решение:

Имеем неполный моментный ряд. Средний уровень такого ряда исчисляют по формуле средней хронологической взвешенной.

, где

- средние уровни интервала между датами;

t – величина интервала времени (число месяцев или дней между моментами времени).

Чтобы воспользоваться этой формулой, нужно превратить моментный ряд в интервальный:

	у	Длина периода, месяцев	Средний уровень товарных запасов в интервалах между датами ()
1,1 1,5 1,8 1,11	61,1 57,5 51,3 74,7	-	-

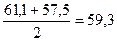
Средний уровень товарных запасов за год составит:

тыс. руб.

№6. За январь месяц произошли следующие изменения в списочном составе работников предприятия, чел.:

Состояло по списку на 1.1 Выбыло с 5.1 Зачислено с 12.1 Зачислено с 26.1

Необходимо определить среднюю дневную списочную численность работников предприятия за январь.

Решение:

Запишем данные в виде ряда:

	Число работников, чел. (у)
1.1 5.1 12.1 26.1

Это неполный моментный ряд динамики. Для определения среднего уровня такого ряда динамики используют среднюю арифметическую взвешенную:

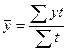, где

у – уровни, сохраняющиеся без изменения в течение промежутков времени t;

t – продолжительность каждого календарного периода с постоянной численность работающих.

Для расчета средней численности работников определим продолжительность t каждого календарного периода с постоянной численностью работающих и общее число человеко-дней.

	Длина периода, месяцев, t	Число человекo-дней, yt
1.1 5.1 12.1 26.1

Среднедневная списочная численность работников в январе:

чел.

№7. Имеются данные о выпуске продукции «А» по месяцам отчетного года.

Месяц	Январь	Февраль	Март	Апрель	Май	Июнь
Выпуск продукции, тыс. шт.	40,2	38,8	37,1	34,4	34,4	31,0

Необходимо рассчитать аналитические показатели ряда динамики.

Решение:

Простейшими показателями, которые используются при измерении скорости изменения уровней ряда динамики, являются абсолютный прирост (), темп роста (), темп прироста (), а также абсолютное значение одного процента прироста (А), пункты роста.

В зависимости от задачи исследования абсолютные приросты, темы проста и темпы прироста в моментных и интервальных рядах с равностоящими уровнями (полных) могут быть исчислены с переменной базой сравнения (в этом случае их называют цепными) и с постоянной базой сравнения (в этом случае их называют базисными).

Абсолютный прирост () характеризует абсолютную скорость роста, показывает, на сколько единиц увеличился (или уменьшился) уровень данного периода или момента времени по сравнению с предыдущим (или базисным) уровнем.

Абсолютный прирост может быть положительным, отрицательным и равным нулю.

Цепной абсолютный прирост-это разность между последующим уровнем ряда и предыдущим уровнем.

. Подсчитываем в гр. 2 табл. 5.1.

Базисный абсолютный прирост – это разность между последующим уровнем и базисным.

. Подсчитываем в гр. 3 табл.5.1.

Знак «-» свидетельствует о снижении выпуска продукции. Из полученных значений видно, что по месяцам периода происходило систематическое возрастание абсолютного снижения выпуска продукции, причем базисные и цепные показатели абсолютной убыли показывают, что в снижении выпуска продукции имело место замедление в мае месяце.

Между цепными и базисными абсолютными приростами существует взаимосвязь.

Каждый базисный абсолютный прирост равен сумме цепных абсолютных приростов и каждый цепной абсолютный прирост равен разности соответствующих базисных абсолютных приростов.

Интенсивность изменения уровней оценивается отношением уровней. Относительными показателями динамики, характеризующими интенсивность изменения уровней являются темпы роста и прироста. Выражаются темпы роста в коэффициентах или процентах.

Цепной темп роста исчисляют отношением последующего уровня у предыдущему:

(расчет см. гр.4. табл.5.1).

Базисный – отношением каждого последующего уровня к базисному уровню

(расчет см. гр.5. табл.5.1).

Темпы роста – только положительные числа.

Темпы роста (Т) (снижения) показывают, во сколько раз уровень данного периода или момента времени больше предыдущего или базисного уровня (если Т>1) или какую часть предыдущего или базисного уровня составляет уровень данного периода или момента времени (если Т<1).

Между цепными и базисными темпами роста имеется взаимосвязь:

- каждый базисный темп роста равен произведению соответствующий цепных темпов роста;

- каждый цепной темп роста равен отношению последующего базисного к предыдущему.

Темп прироста (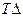) (сокращения) показывает, на сколько процентов уровень данного периода или момента времени больше (или меньше) предыдущего или базисного уровня.

Цепной темп прироста () определяется двумя способами:

1) отношением цепного абсолютного прироста к предыдущему уровню

2) или (расчет см. гр.6. табл.5.1.)

Базисный темп прироста () определяется двумя способами:

1) отношением базисного абсолютного прироста к базисному уровню:

2) (расчет см. гр. 7 табл.5.1.)

Темп прироста может быть положительным, отрицательным и равным нулю.

Между взаимосвязи не существует, их нельзя суммировать и перемножать.

Пункты роста (П_р) (их иногда называют темпами наращивания) определяются двумя способами:

1) делением цепных абсолютных приростов на базисный уровень

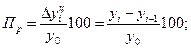
2) разностью между базисными темпами роста:

(расчет см. гр.8. табл.5.1.)

В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно суммировать, в результате получая базисный темп прироста соответствующего периода. Например, сумма пунктов роста равна – 22,9 (), соответствует темпу прироста выпуска продукции в июне по сравнению с январем.

Таблица 5.1

Годы	Выпуск продукции, тыс. шт.	Абсолютные приросты, тыс. шт.	Темпы роста (снижения), в коэффициентах	Темпы прироста (сокращения)	Пункты роста, % 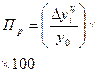или	Абсолютное значение 1% прироста, тыс. руб. или

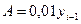
А
Январь	40,2	-	-	-	1,000	-	-	-	-
Февраль	38,8	37,1 - 40,2 = - 1,4	37,1 - 40,2 = - 1,4	38,8/40,2= =0,965	38,8/40,2= =0,965	96,5-100=3,5	96,5-100=3,5	96,5-100=3,5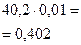
Март	37,1	37,1-38,8 = - 1,7	37,1-40,2=-3,1	37,1/38,8= =0956	37,1/40,2= =0,923	95,6-100=-7,7	95,6-100=-7,7	92,3-96,5=-4,2	0,388
Апрель	34,4	-2,7	- 5,8	0,927	0,856	-7,3	-14,4	85,6-92,3=-6,7	0,371
Май	34,4		- 5,8	1,000	0,856		-14,4		0,344
Июнь	31,0	-3,4	-9,2	0,901	0,771	-9,9	-22,9	-8,5	0,344
			-	=0,771	-	-