Показатели тесноты связи альтернативных признаков

 

Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из 2-х групп (т.е. имеет альтернативный характер), применяются коэффициенты ассоциации и контингенции. При исследовании связи исходные данные располагают в комбинационной четырех клеточной таблице (таблице четырех полей), например, табл. 7.8:

Таблица 7.8

Таблица для вычисления коэффициентов ассоциации и контингенции

Группы по признаку Б   Группы по признаку А
	a	b	a + b
	c	d	c + d
	a + c	b + d	a + b + c + d

 

Если обозначим данные в каждой из четырех клеток латинскими буквами a,b,c,d, то получим следующие формулы расчета коэффициентов:

коэффициент ассоциации ():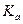

 

коэффициент контингенции ():

 

.

 

Коэффициент контингенции всегда меньше коэффициента ассоциации, связь считается подтвержденной, если , а .

№2. Исследовалась связь между выполнением норм выработки рабочими предприятия и их технически обучением. Результаты обследования характеризуются следующими данными:

Таблица 7.9

Зависимость выполнения норм выработки рабочими от их технического обучения

 

Группы рабочих по выполнению норм   Группы рабочих по техническому обучению	Число рабочих
Выполнивших и перевыполнивших норму	Не выполнивших норму	Всего
Прошедшие техническое обучение
Не прошедшие техническое обучение
Всего

 

 

Так как , а , можно говорить о наличии существенной связи между выполнением норм рабочими и их техническим обучением.

 

№3. Имеются следующие данные:

Таблица 7.10

 

Номер предприятия
Электровооруженность труда на 1 работающего, кВт. ч.
Выпуск готовой продукции на 1 работающего, тыс. руб.

 

Рассчитайте параметры линейного уравнения зависимости выпуска готовой продукции на 1 работающего от энерговооруженности труда. Покажите эмпирические и теоретические линии регрессии на графике. Определите степень тесноты связи между этими признаками.

Решение:

Зависимость между электровооруженностью труда и продукцией на одного работающего – линейная и выражается уравнением прямой:

 

,

где - выпуск готовой продукции на одного работающего;

х – электровооруженность труда на одного работающего;

- параметры уравнения регрессии.

Параметры уравнения прямой 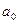, определяются путем решения системы нормальных уравнений, полученных по методу наименьших квадратов:

,

.

 

Для определения параметров уравнения регрессии строим расчетную таблицу 7.11:

Таблица 7.11

№ предприятия	Электровооруженность труда на 1 работающего, кВт.ч., х	Выпуск готовой продукции на 1 работающего, тыс. руб., у	ху	х2	у2
						3,61 6,00 4,41 7,59 3,61 6,80	-0,61 -0,41 -1,59 0,39 1,20	0,372 0,618 2,528 0,152 1,440

Продолжение таблицы 7.11

 

						5,20 9,19 8,39 5,20	0,80 -0,19 0,6 -0,2	0,640 0,036 0,384 0,040
Итого							-	5,760
В среднем					-	-	-	-

 

Подставим в систему нормальных уравнений фактические данные из таблицы:

 

 

I способ.

Решаем систему нормальных уравнений в следующей последовательности:

Домножим каждый член первого уравнения на 5

 

 

,

 

вычтем из второго уравнения первое и получим

 

, откуда .

 

Подставим значение в первое уравнение

 

,

получим 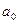=2,02.

Уравнение корреляционной связи примет вид

 

.

II способ.

Параметры уравнения регрессии можно определять по формулам:

 

,

 

.

 

III способ.

 

, где ; ; .

 

Для определения параметров этим способом строим расчетную таблицу 7.12:

 

Таблица 7.12

 

№ предприятия	х	у
			-3 -2 -3 -1 -1		-3 -2 -1
Итого

 

;

.

 

Корреляционное уравнение .

После определения параметров уравнения регрессии рассчитываем теоретическую линию регрессии путем подстановки значений х в уравнение корреляционной связи:

;

 

, и т.д.

 

Если параметры уравнения связи определены правильно, то .

Окончательная проверка правильности расчета параметров уравнения связи производится подстановкой 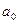и в систему нормальных уравнений.

Используя уравнение связи можно определить теоретическое значение для любой промежуточной точки (теоретическое значение выпуска готовой продукции на 1 работающего для любого промежуточного значения электровооруженности труда).

Коэффициент регрессии уточняет связь между х и у. Он показывает, на сколько единиц увеличивается результативный признак при увеличении факторного признака на единицу. В нашем примере =0,796. Значит, при увеличении электровооруженности труда на 1 работающего на 1 кВт. ч. выпуск продукции увеличится на 0,796 тыс. руб.

Построим эмпирическую и теоретическую линии регрессии на графике:

 

 

Рис. 7.3 Зависимость выпуска готовой продукции на 1 работающего от электровооруженности труда

эмпирическая линия регрессии

теоретическая линия регрессии

 

 

При линейной зависимости между признаками для определения тесноты корреляционной связи применяются коэффициент корреляции (r) и индекс корреляции (R)

Наиболее удобной формулой для расчета коэффициента корреляции является следующая:

1) ,

 

r изменяется от – 1 до +1 и показывает тесноту и направление корреляционной связи. В нашем примере r=0,925, что показывает весьма тесную прямую связь между электровооруженностью труда рабочих и их производительностью труда.

Коэффициент корреляции можно рассчитывать и по другим формулам:

 

2) ,

 

где

 

 

3) .

 

4) если определена форма корреляционной связи и вычислен коэффициент регрессии , линейный коэффициент можно определить, используя формулу:

 

.

5) Индекс корреляции удобно рассчитать по формуле:

,

- остаточная дисперсия характеризующая вариацию результативного признака от всех прочих, кроме х, факторов, определяется

 

;

 

- общая дисперсия, отображающая совокупное влияние всех факторов:

 

;

 

.

 

По абсолютной величине линейный коэффициент корреляции r и индекс корреляции R при прямолинейной связи совпадают.

 

№ 4. По результатам решения типовой задачи №3 дать оценку типичности параметров уравнения и значимости показателей тесноты связи.

 

Решение:

1. Применительно к совокупностям, у которых n<30, для проверки типичности параметров уравнения регрессии используется t–критерий Стьюдента. При этом вычисляются фактические значения t–критерия по формулам:

для параметра :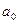

;

для параметра :

.

Полученные фактические значения , сравниваются с критическим , которые получают по таблице Стьюдента с учетом принятого уровня значимости и числа степеней свободы (см. приложение 6).

Полученные в анализе корреляционной связи параметры уравнения регрессии признаются типичными, если t фактическое больше t критического:

 

.

 

Подсчитаем фактические значения t–критерия Стьюдента. Для определения среднего квадратического отклонения результативного признака у от выравненных значений воспользуемся формулой:

.

 

Среднее квадратическое отклонение факторного признака х от общей средней 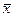определим по формуле:

 

 

Фактические значения t – критерия равны:

 

,

 

 

С учетом принятого в экономико-статистических исследованиях уровня значимости =0,05 и числа степеней свободы табличное критическое значение =2,307 (см. приложение 6).

Сравним фактические и табличное значения t – критерия:

 

.

 

Это позволяет признать вычисленные по уравнению параметры типичными.

2. Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности.

Для оценки значимости коэффициента корреляции r применяется t–критерий Стьюдента. При этом определяется фактическое значение критерия :

 

.

 

Фактическое значение сравниваются с критическими , которое берется из таблицы значений t–критерия Стьюдента с учетом заданного уровня значимости и числа степеней свободы к.

Если > то величина коэффициента корреляции признается существенной. В нашем примере r=0,925, фактическое значение критерия

 

 

При критическом значении =2,307 получается. > . Поэтому вычисленный коэффициент корреляции признается существенным.

Из значения 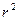=0,856 следует, что 85,6 % общей вариации производительности труда объясняется изменением электровооруженности труда. Поэтому корреляционное уравнение может быть использовано для практических целей.

Для оценки значимости индекса корреляции 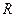применяется 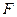критерий Фишера.

Фактическое значение критерия определяется по формуле

 

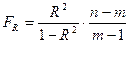
Величина сравнивается с критическим , которое определяется по таблице 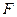критерия с учетом принятого уровня значимости и числа степеней свободы и . Если > , то величина индекса корреляции признается существенной. Подсчитаем :

 

 

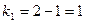При уровне значимости =0,05 и степенях свободы и табличное значение =5,32 (См. приложение 7). Следовательно, =47,6 > =5,32. Поэтому показатель тесноты связи 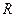= 0,925 принимается существенным.

 

Задачи

№7.1 Исследуйте зависимость роста производительность труда от роста фондовооруженности (прирост в %)

 

Производительность труда
Фондовооруженность

 

Представьте на графике эмпирическую и теоретическую зависимости и сделайте выводы.

 

№7.2 Имеются следующие данные об уровне энерговооруженности труда и себестоимости продукции:

 

Энерговооруженность труда, кВт
Себестоимость 1 ед. продукции тыс. руб.

 

1. Рассчитайте параметры линейного уравнения зависимости себестоимости продукции от энерговооруженности труда.

2. Покажите эмпирические и теоретические линии регрессии на графике.

3. Определите степень тесноты связи между признаками с помощью индекса корреляции.

4. Дайте оценку типичности параметров уравнения и значимости индекса корреляции.

 

 

№7.3 Имеются следующие данные по предприятиям за отчетный год:

 

Среднегодовая стоимость основных промышленно-производственных фондов, млн. руб.
Фактический выпуск продукции, млн. руб.

 

Рассчитайте параметры линейного уравнения связи и дайте оценку их типичности. Сделайте выводы.

 

 

№ 7.4 Имеются следующие данные о стаже и выработке рабочих бригады:

 

Номер рабочего	Стаж, лет	Выработка (шт.)	ух

 

Для измерения тесноты корреляционной связи между стажем и выработкой рабочих рассчитайте индекс корреляции. Дайте оценку его значимости с помощью критерия Фишера. Сделайте выводы.

 

 

№ 7.5 Имеются следующие данные по группе предприятий:

 

 

№ предприятия п/п	Основные производственные фонды, млн. руб.	Объем продукции, млн. руб.

 

По исходным данным определите линейное уравнение корреляционной связи между размером основных фондов и выпуском продукции. Дайте оценку типичности параметров с помощью критерия Стьюдента.

Сделайте выводы.

 

№7.6 Имеются следующие данные:

 

Стаж рабочего в годах	Выработка изделий за смену, шт

 

Для установления характера связи между стажем работы и производительностью труда вычислите линейное уравнение связи. Поясните смысл коэффициента регрессии. Для характеристики тесноты связи вычислите линейный коэффициент корреляции. Дайте оценку типичности параметров уравнения и значимости линейного коэффициента корреляции.

 

Приложение 1

 

 

Приложение 2

 

 

Приложение 3

 

Формулы для расчета предельной ошибки при различных видах выборки

 

Вид выборки	Повторный отбор	Бесповторный отбор
для средней	для доли	для средней	для доли
Собственно случайная
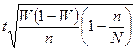
Механическая	Используются формулы собственно- случайной выборки
Типическая
Серийная

- предельная ошибка выборки; .

 

 

Приложение 4

 

Формулы для расчета численности выборки при различных видах выборки

 

Вид выборки	Повторный отбор	Бесповторный отбор
для средней	для доли	для средней	для доли
Собственно случайная
Механическая	Применяются формулы собственно- случайной выборки
Типическая
Серийная

 

 

Приложение5

Таблица значений интеграла вероятностей

 

 

t
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0

 

Все числа увеличены в 10 тысяч раз.

 

Приложение 6

 

Таблица значения t Стьюдента для =0,05 и 0,01

 

Число степеней свободы	=0,05	=0,01	Число степеней свободы	=0,05	=0,01
	12,69 4,302 3,183 2,777 2,571 2,447 2,364 2,307 2,263 2,227 2,200 2,179 2,161 2,145 2,131 2,119 2,110 2,100 2,093 2,086	63,655 9,924 5,841 4,604 4,032 3,707 3,500 3,356 3,250 3,169 3,138 3,055 3,012 2,977 2,946 2,921 2,898 2,877 2,860 2,846		2,078 2,074 2,069 2,064 2,059 2,054 2,052 2,049 2,045 2,042 2,037 2,032 2,027 2,025 2,020 2,017 2,015 2,012 2,010 2,007 2,005 2,000	2,832 2,818 2,807 2,796 2,787 2,778 2,771 2,764 2,757 2,750 2,739 2,728 2,718 2,711 2,704 2,696 2,691 2,685 2,681 2,678 2,668 2,661

 

Приложение 7

Критические значения F- критерия

 

Уровень значимости =0,05
	161,4 18,51 10,13 7,71 6,61 5,99 5,59 5,32 5,12 4,96 4,82 4,75 4,60 4,49 4,41 4,35 4,17 4,08 4,00 3,92 3,84	199,5 19,00 9,45 6,94 5,79 5,14 4,74 4,46 4,26 4,10 3,98 3,88 3,74 3,63 3,55 3,49 3,32 3,23 3,15 3,07 2,99	215,7 19,16 9,28 6,59 5,41 4,76 4,35 4,07 3,86 3,71 3,59 3,49 3,34 3,24 3,16 3,10 2,92 2,84 2,76 2,68 2,60	224,6 19,25 9,12 6,39 5,19 4,53 4,12 3,84 3,63 3,48 3,63 3,26 3,11 3,01 2,93 2,87 2,69 2,61 2,52 2,45 2,37	230,2 19,30 9,01 6,26 5,05 4,39 3,97 3,69 3,48 3,33 3,20 3,11 2,96 2,85 2,77 2,71 2,53 2,45 2,37 2,29 2,21	234,0 19,33 8,94 6,16 4,95 4,28 3,87 3,58 3,37 3,22 3,09 3,00 2,85 2,74 2,66 2,60 2,42 2,34 2,25 2,17 2,09	238,9 19,37 8,84 6,04 4,82 4,15 3,73 3,44 3,23 3,07 2,95 2,85 2,70 2,59 2,51 2,45 2,27 2,18 2,10 2,02 1,94	242,0 19,39 8,78 5,96 4,74 4,06 3,63 3,34 3,13 2,97 2,86 2,76 2,60 2,49 2,41 2,35 2,16 2,12 2,04 1,90 1,83	248,0 19,44 8,66 5,80 4,56 3,87 3,44 3,15 2,93 2,77 2,65 2,54 2,39 2,28 2,19 2,12 1,93 1,84 1,75 1,65 1,57
Уровень значимости =0,01
	98,49 34,12 21,20 16,26 13,74 12,25 11,26 10,56 10,04 9,65 9,33 8,86 8,58 8,28 8,10 7,56 7,31 7,08 6,85 6,64	99,00 30,81 18,00 13,27 10,92 9,55 8,65 8,02 7,56 7,20 6,93 6,51 6,23 6,01 5,85 5,39 5,18 4,98 4,79 4,60	99,17 29,46 16,69 12.06 9,78 8,45 7,59 6,99 6,55 6,22 5,95 5,56 5,29 5,09 4,94 4,51 4,31 4,13 3,95 3,78	99,25 28,71 15,98 11,39 9,15 7,85 7,01 6,92 5,99 5,64 5,41 5,03 4,77 4,58 4,43 4,02 3,83 3,65 3,48 3,32	99,30 28,24 15,52 10,97 8,75 7,46 6,63 6,02 5,64 5,32 5,06 4,69 4,44 4,25 4,10 3,70 3,51 3,34 3,17 3,02	99,33 27,91 15,21 10,67 8,47 7,19 6,37 5,80 5,39 5,07 4,82 4,46 4,20 4,01 3,87 3,47 3,29 3,12 2,96 2,80	99,36 27,49 14,80 10,27 8,10 6,84 6,03 5,47 5,06 4,74 4,50 4,14 3,89 3,71 3,56 3,17 2,99 2,82 2,66 2,51	99,40 27,23 14,54 10,05 7,87 6,62 5,82 5,26 4,85 5,54 4,30 3,94 3,69 3,51 3,37 2,98 2,80 2,63 2,47 2,32	99,45 26,69 14,02 10,55 7,39 6,15 5,36 4,80 4,41 4,10 3,86 3,51 3,25 3,07 2.94 2,55 2,37 2,20 2,03 1,87

Приложение 8

Статистические таблицы

Таблица – это форма наиболее рационального изложения цифрового материала.

Таблица имеет подлежащее и сказуемое.

Подлежащее таблицы - это объект изучения.

Сказуемое – это система показателей, которыми характеризуется объект изучения.

 

 

⇐ Предыдущая12345678

Поделиться:

Воспользуйтесь поиском по сайту: