 |
Основные статистические методы изучения взаимосвязей
|
|
|
|
После того как с помощью теоретического анализа выяснена сущность явлений и возможность связи между ними, установлены факторный и результативный признаки, необходимо определить направление и характер связи, выявить форму воздействия одних факторов на другие и дать ей количественную оценку. Для выявления наличия связи, характера и направления в статистике используются методы: сравнения параллельных рядов, аналитической группировки, графический. Для выявления формы воздействия одних факторов на другие используют регрессионный анализ, а количественную оценку силы воздействия дают с помощью корреляционного анализа.
Метод сравнения параллельных рядов основан на сопоставлении двух или нескольких рядов показателей. Сущность этого метода состоит в том, что сначала показатели характеризующие факторный признак, располагаются в порядке возрастания или убывания (ранжируются), а затем параллельно им располагаются соответствующие показатели результативного признака. Сравнение построенных таким образом рядов дает возможность не только подтвердить само наличие связи, но и выявить ее направление и характер.
Например, возьмем данные по 15 коммерческим банкам региона о размере собственных средств ((х), млн. руб.) и о размере привлеченных средств ((у), млн. руб.). Данные эти сведены в табл. 7.2, где банки расположены в порядке возрастания размера собственных средств:
Таблица 7.2
Размер собственных (х) и привлеченных (у) средств по 15 банкам региона
| № п/п | х | у | № п/п | х | у | № п/п | х | у |
Рассматривая данные таблицы, видим, что с возрастанием признака х, размера собственных средств, растет (правда, не всегда) признак у – размер привлеченных средств. Следовательно, между х и у имеется прямая статистическая (статистическая) зависимость.
|
|
|
Возрастание объема привлеченных средств с частыми отклонениями говорит о влиянии на этот показатель других факторов помимо объема собственных средств.
Графический метод рекомендуется применять для предварительного анализа и оценок. Так, выявленную с помощью сравнения параллельных рядов связь между объемом собственных (х) и привлеченных средств (у) банков можно наглядно увидеть, если построить график, отложив на оси абсцисс значение признака х, а на оси ординат – значение признака у. Нанеся на график точки, соответствующие значениям х и у, получим корреляционное поле (рис. 7.1), где по характеру расположения точек можно судить о направлении и силе связи.
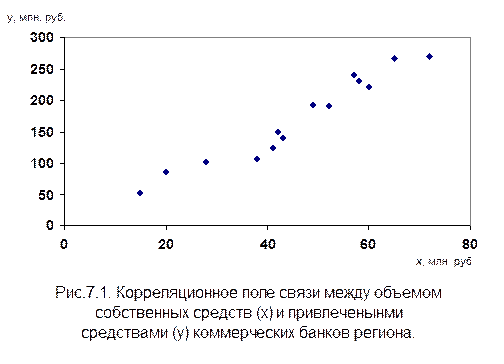 |
Если точки беспорядочно разбросаны по всему полю, это говорит о том, что зависимости между двумя признаками нет, если они будут концентрироваться вокруг оси, идущей от нижнего левого угла в верхний правый, то имеется прямая зависимость между варьирующими признаками; если точки будут концентрироваться вокруг оси, идущей от верхнего левого угла в нижний правый, то имеется обратная зависимость.
В нашем примере корреляционное поле ясно показывает, что имеется тенденция к росту из левого нижнего угла в правый верхний. Значит, имеется прямая корреляционная зависимость между объемом собственных средств и привлеченными средствами коммерческих банков региона.
Стохастическая связь будет проявляться отчетливее, если применить для выявления ее наличия и направления метод аналитической группировки. Он состоит в том, что совокупность единиц разбивается на группы по величине факторного признака и по каждой группе исчисляется средняя величина результативного признака. Вариация средней величины результативного признака от группы к группе под влиянием изменения факторного признака будет указывать на наличие, характер и направление связи.
|
|
|
В нашем примере произведем аналитическую группировку коммерческих банков региона по объему собственных средств и по каждой группе исчислим средний объем привлеченных средств. Образуем четыре группы с равными интервалами. Размер интервала определим по формуле:
 млн. руб.
млн. руб.
Все расчеты проделаем в рабочей таблице 7.3:
Таблица 7.3
Распределение банков по объему собственных средств
| № п/п | Группы банков по объему собственных средств, млн. руб. | № банка и число банков | Объем собственных средств, млн. руб., х | Объем привлеченных средств, млн. руб., у |
| А | Б | |||
| I | 15-30 | |||
| Итого: | ||||
| II | 30-45 | |||
| Итого | ||||
| III | 45-60 | |||
| Итого | ||||
| IV | 60-75 | |||
| Итого | ||||
| Всего |
Затем групповые показатели рабочей таблицы и исчисленные на их основе средние показатели заносим в построенную итоговую аналитическую таблицу (табл.7.4), и увидим, изменяются эти средние в прямом соответствии с изменением объема собственных средств или нет.
Таблица 7.4
Зависимость объем привлеченных средств (у)
от объема собственных средств (х)
| Группы банков по объему собственных средств (х), млн. руб. | Число банков f | Объем собственных средств, млн. руб. | Объем привлеченных средств, млн. руб. | ||
| всего | В среднем на банк 
| всего | В среднем на банк 
| ||
| А | |||||
| 15-30 30-45 45-60 60-75 | |||||
| Итого: | 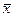 = 47,7 = 47,7
| 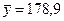
|
Данные табл. 7.4 показывают, что с ростом значений факторного признака (объем собственных средств) растет (закономерным образом изменяется) среднее значение результативного признака у (средний объем привлеченных средств банк), следовательно, между х и у имеется прямая корреляционная зависимость.
Прежде чем применять корреляционно-регрессионный анализ для определения формы связи, исчисления ее количественной характеристики и измерения степени тесноты связи, нужно предварительно отобрать факторы, оказывающие существенное влияние на результативный признак. Помочь в этом может метод аналитической группировки и расчет на его основе эмпирического корреляционного отношения.
|
|
|
Эмпирическое корреляционное отношение (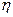 ) равно корню квадратному из эмпирического коэффициента детерминации (
) равно корню квадратному из эмпирического коэффициента детерминации (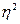 ):
):
 .
.
Коэффициент детерминации (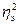 ) показывает, какая часть общей вариации (дисперсии) результативного признака у объясняется вариацией группировочного фактора х, определяется отношением межгрупповой дисперсии к общей диспресии результативного признака:
) показывает, какая часть общей вариации (дисперсии) результативного признака у объясняется вариацией группировочного фактора х, определяется отношением межгрупповой дисперсии к общей диспресии результативного признака:
 .
.
Межгрупповая дисперсия результативного признака (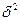 ), характеризующая его вариацию за счет группировочного признака х, исчисляется по формуле:
), характеризующая его вариацию за счет группировочного признака х, исчисляется по формуле:
 ,
,
где  - групповые средние результативного признака у;
- групповые средние результативного признака у;
 - общая средняя результативного признака;
- общая средняя результативного признака;
f – число единиц в группах.
Общая дисперсия (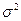 ), характеризующая его вариацию за счет всех факторов, исчисляется по формулам:
), характеризующая его вариацию за счет всех факторов, исчисляется по формулам:
1)  ; 2)
; 2)  .
.
Таблица 7.5
Расчет межгрупповой дисперсии результативного признака (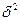 )
)
Объем привлеченных средств, млн. руб. в среднем на банк, 
| Число банков, f | 
|

| ||

| ||
| 4651,24 | ||
| 31755,24 | ||
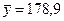
| 75314,95 |
 .
.
Таблица 7.6
Расчет общей дисперсии объема привлеченных средств (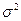 )
)
| № банка | у | 
| 
| № банка | у | 
| 
|
| -126,9 -92,9 -76,9 -72,9 -54,9 -28,9 -38,9 13,1 | 16103,61 8630,41 5913,61 5314,41 3014,01 835,21 1513,21 171,61 | 11,1 61,1 51,1 41,1 88,1 91,1 136,1 | 123,21 3733,21 2611,21 1689,21 7761,61 8299,21 18523,21 | ||||
| Итого | 84236,95 |
Подсчитаем общую дисперсию результативного признака:
 .
.
Следовательно, коэффициент детерминации 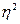 , показывающий роль группировочного признака в образовании общей вариации, составит:
, показывающий роль группировочного признака в образовании общей вариации, составит:
 .
.
Это означает, что вариация привлеченных средств у 15 банков на 89,4% обусловлена объемом собственных средств банков и на 10,6 %- другими факторами.
Эмпирическое корреляционное отношение (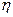 ) равно:
) равно:
 , что означает сильную степень тесноты связи.
, что означает сильную степень тесноты связи.
Убедившись в этом, можно перейти к корреляционно-регрессионному анализу и прежде всего к поискам функции теоретической линии связи, параметры которой при достаточно высокой степени тесноты связи могут быть использованы в управлении.
|
|
|
|
|
|


