 |
Дополнительная. Конспект лекций по дисциплине «Эконометрика»
|
|
|
|
Дополнительная
1. Катышев, П. К. Сборник задач к начальному курсу эконометрики / П. К. Катышев, А. А. Пересецкий. – М.: Дело, 2009. -408 с.
2. Кобелев Н. Б. Практика применения экономико-математических методов и моделей: учеб. практ. пособие – М.: ЗАО «Финстатинформ», 2007. -157 с.
3. Новак, Э. Введение в методы эконометрики / сборник задач – М.: Финансы и статистика, 2008. – 248 с.
4. Сигел, Э. Практическая бизнес-статистика. – М.: Издательсткий дом «Вильямс», 2009. -1056 с.
5. Шикин, Е. В. Математические методы и модели в управлении. / Е. В. Шикин, А. Г. Чхартишвили. – М.: Дело, 2007. -438 с.
Конспект лекций по дисциплине «Эконометрика»
1. ПРЕДМЕТ ЭКОНОМЕТРИКИ
Эконометрика – быстроразвивающаяся отрасль науки, цель которой состоит в том, чтобы придать количественные меры эконометрическим отношениям.
Термин «эконометрика» был впервые введен в Австро-Венгрии в 1910 г. Считалось, что если к данным бухгалтерского учета применить методы алгебры и геометрии, то будет получено новое, более глубокое представление о результатах хозяйственной деятельности. Это употребление термина, как и сама концепция, не прижилось, но название «эконометрика» оказалось весьма удачным для определения нового направления в экономической науке, которое выделилось в 1930 г.
Слово «эконометрика» представляет собой комбинацию двух слов: «экономика» и «метрика» (от греч. «метрон»). Таким образом, сам термин подчеркивает специфику, содержание эконометрики как науки: количественное выражение тех связей и соотношений, которые раскрыты и обоснованы экономической теорией.
Зарождение эконометрики является следствием междисциплинарного подхода к изучению эконометрики. Эта наука возникла в результате взаимодействия и объединения в особый «сплав» трех компонентов: экономической теории, статистических и математических методов. Впоследствии к ним присоединилось развитие вычислительной техники как условие развития эконометрики.
|
|
|
2. ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ
В ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЯХ
В эконометрике широко используются методы статистики. Ставя цель дать количественное описание взаимосвязей между экономическими переменными, эконометрика прежде всего связана с методами регрессии и корреляции.
В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.
Простая регрессия представляет собой регрессию между двумя переменными – y и x, т. е. модель вида
 ,
,
где y – зависимая переменная (результативный признак);
x – независимая, или объясняющая, переменная (признак-фактор).
Множественная регрессия соответственно представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида
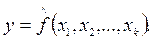
Любое эконометрическое исследование начинается со спецификации модели, т. е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. Иными словами, исследование начинается с теории, устанавливающей связь между явлениями.
Прежде всего, из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Предположим, что выдвигается гипотеза о том, что величина спроса  на товар А находится в обратной зависимости о цены
на товар А находится в обратной зависимости о цены  , т. е.
, т. е.  . В уравнении регрессии корреляционная связь признаков представляется в виде функциональной связи, выраженной математической функцией. Обратная зависимость результата от фактора не обязательно характеризуется линейной функцией
. В уравнении регрессии корреляционная связь признаков представляется в виде функциональной связи, выраженной математической функцией. Обратная зависимость результата от фактора не обязательно характеризуется линейной функцией
|
|
|

Возможны и другие соотношения, например:

 ;
; 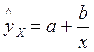 ;
; 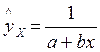
От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака  подходят к фактическим данным
подходят к фактическим данным  .
.
Линейная регрессия находит широкое применение в эконометрике в виде четкой экономической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида



Уравнение вида  позволяет по заданным значениям фактора
позволяет по заданным значениям фактора  иметь теоретические значения результативного признака, подставляя в него значения фактора
иметь теоретические значения результативного признака, подставляя в него значения фактора  . На графике теоретические значения представляют линию регрессии (рис. 1).
. На графике теоретические значения представляют линию регрессии (рис. 1).
Построение линейной регрессии сводиться к оценке ее параметров – 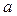 и
и  . Оценка параметров линейной регрессии может быть найдено разными методами. Можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию (см. рис. 1). Далее по графику можно определить значения параметров. Параметр
. Оценка параметров линейной регрессии может быть найдено разными методами. Можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию (см. рис. 1). Далее по графику можно определить значения параметров. Параметр 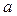 определим как точку пересечения линии регрессии с осью
определим как точку пересечения линии регрессии с осью  , а параметр
, а параметр  оценим, исходя из угла наклона линии регрессии, как
оценим, исходя из угла наклона линии регрессии, как  , где
, где  - приращение результата
- приращение результата  , а
, а 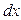 -приращение фактора
-приращение фактора  , т. е.
, т. е.

Рис. 1. Графическая оценка параметров линейной регрессии
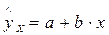
Преобразуя формулу, получим следующую систему нормальных уравнений для оценки параметров 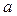 и
и  :
:

Решая систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров 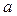 и
и  . Информация, необходимая для расчета оценок параметров
. Информация, необходимая для расчета оценок параметров 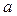 и
и  , представлена в табл. 1.
, представлена в табл. 1.
Таблица 1
Расчетная таблица
| № предприятия | Выпуск продукции, тыс. ед. (  ) )
| Затраты на производство, млн. руб. (  ) )
| 
| 
| 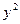
| 
|
| 31, 1 67, 9 141, 6 104, 7 178, 4 104, 7 141, 6 | ||||||
| Итого | 770, 0 |
Система нормальных уравнений будет иметь вид

Решая ее, получим:


Запишем уравнение регрессии:

Различают два класса нелинейных регрессий:
|
|
|
- регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
- регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:
- полиномы разных степеней - 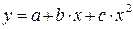 ,
, 
- равносторонняя гипербола -  .
.
К нелинейным регрессиям по оцениваемым параметрам относятся функции:
- степенная -  ;
;
- показательная -  ;
;
- экспоненциальная -  .
.
Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, ибо эти функции линейны по параметрам. Так, в параболе второй степени
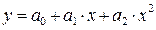
Применение уже использованного метода для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:

Таблица 2
Зависимость доходов предприятия от размера затрат на рекламу
Размер затрат на рекламу, тыс. руб, 
| Доход, млн, руб, 
| 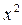
| 
| 
| 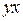
| 
| 
|
| 6, 2 8, 5 10, 4 11, 9 13, 0 | |||||||

| 50, 0 |
По данным табл. система нормальных уравнений составит:

Решая ее методом определителей, получим:  ,
,  ,
,  ,
,  . Откуда параметры искомого уравнения составят:
. Откуда параметры искомого уравнения составят: 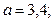

 , а уравнение параболы второй степени примет вид
, а уравнение параболы второй степени примет вид
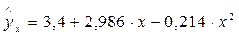
Поставляя в это уравнение последовательно значения  , найдем теоретические значения
, найдем теоретические значения 
Среди класса нелинейных функций, параметры которых оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу: 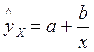 .
.
Она может быть использована не только для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота, т. е. на микроуровне, но и макроуровне. Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы  и процентом прироста заработной платы
и процентом прироста заработной платы  :
:
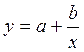
Английский экономист А. В. Филипс, анализируя данные более чем за 100-летний период, в конце 50-х гг. XX в. установил обратную зависимость процента прироста заработной платы от уровня безработицы.
|
|
|
Для равносторонней гиперболы вида 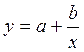 заменив
заменив  на
на 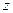 , получим линейное уравнение регрессии
, получим линейное уравнение регрессии 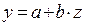 , оценка параметров которого может быть дана МНК. Система нормальных уравнений составит:
, оценка параметров которого может быть дана МНК. Система нормальных уравнений составит:
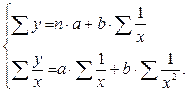
3. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Вместе с тем исследователь никогда не может быть уверен в справедливости данного предположения. Для того чтобы иметь правильное представление о влиянии дохода на потребление, необходимо изучить их корреляцию при неизменном уровне других факторов. Прямой путь решения такой задачи состоит в отборе единиц совокупности с одинаковыми значениями всех других факторов, кроме дохода. Он приводит к планированию эксперимента – методу, который используется в химических, физических, биологических исследованиях. Поведение отдельных экономических переменных контролировать нельзя, т. е. не удается обеспечить равенство всех прочих условий для оценки влияния одного исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя их в модель, т. е. построить уравнение множественной регрессии
 .
.
Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функций издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. Множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель множественная регрессия – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
Построение уравнения множественной регрессии начинается с отбора факторов и выбора вида уравнения регрессии.
Включение в уравнение множественной регрессии того или иного набора факторов связано с природой взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
1. Они должны быть количественно измеримы. Если необходимо включать в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место нахождения недвижимости: районы могут быть проранжированы).
|
|
|
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Пусть у=а+б1х1+б2х2, тогда

Таблица
Расчет параметров множественной регрессии
| №п/п | Х1 | Х2 | у | Х1у | Х1х2 | Х21 | Х13 | Х12х2 | Х12у |
| итого |
4. СИСТЕМА ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
При использовании отдельных уравнений регрессии в большинстве случаев предполагается, что аргументы (факторы) можно изменять независимо друг от друга. Однако это предположение является очень грубым: практически изменение одной переменной, как правило, не может происходить при абсолютной неизменности других. Ее изменение повлечет за собой изменение во всей системе взаимосвязанных признаков. Отдельно взятое уравнение множественной регрессии не может характеризовать истинные влияния отдельных признаков на результат. Именно поэтому в последние десятилетия в экономических, биометрических и социологических исследованиях важное место заняла проблема описания структуры связей между переменными системой называемых структурными уравнениями. Так, если изучается модель спроса как соотношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима модель предложения товаров, в которой рассматривается взаимосвязь между количеством и ценой предлагаемых благ.
При оценке эффективности производства нельзя руководствоваться только моделью рентабельности. Она должна быть дополнена моделью производительности труда, а также моделью себестоимости единицы продукции.
Модель национальной экономики включает в себя систему уравнений: функции потребления, инвестиций заработной платы, а также тождество доходов и т. д. Это связано с тем, что макроэкономические показатели, являясь обобщающими показателями состояния экономики, чаще всего взаимозависимы. Так, расходы на конечное потребление в экономике зависят от валового национального дохода. Вместе с тем величина валового национального дохода рассматривается как функция инвестиций.
Система уравнений в эконометрических исследованиях может быть построена по-разному.
Возможна система независимых уравнений, когда каждая зависимая переменная (  ) рассматривается как функция одного и того же набора факторов (
) рассматривается как функция одного и того же набора факторов ( 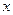 ):
): 

Набор факторов 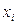 в каждом уравнении может варьировать. Так, модель вида
в каждом уравнении может варьировать. Так, модель вида


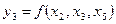

также является системой независимых уравнений с тем лишь отличием, что в ней набор факторов видоизменяется в уравнениях, входящих в систему.
Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется метод наименьших квадратов. По существу, каждое уравнение этой системы является уравнением регрессии.
Однако если зависимая переменная  одного уравнения выступает в виде фактора
одного уравнения выступает в виде фактора  в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:
в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:
Примером такой системы может служить модель производительности труда и фондоотдачи вида:

где 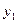 - производительность труда;
- производительность труда;
 - фондоотдача;
- фондоотдача;
 - фондовооруженность труда;
- фондовооруженность труда;
 - энерговооруженность труда;
- энерговооруженность труда;
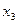 - квалификация рабочих.
- квалификация рабочих.
Как и в предыдущей системе, каждое уравнение может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).
Наибольшее распространение в экономических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входит в левую часть, а в других уравнениях – в правую часть системы:

Система взаимозависимых уравнений получила название система совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные (  ) одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим.
) одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим.
5. ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ ПО ВРЕМЕННЫМ РЯДАМ
Изучение причинно-следственных зависимостей переменных, представленных в форме временных рядов, является одной из самых сложных задач эконометрического моделирования. Применение в этих целях традиционных методов корреляционно-регрессивного анализа может привести к ряду серьезных проблем, возникающих как на этапе построения, так и на этапе анализа эконометрических моделей. В первую очередь эти проблемы связаны со спецификой временных рядов как источника данных в эконометрическом моделировании. Каждый уровень временного ряда содержит три основные компоненты: тенденцию, циклические или сезонные колебания и случайную компоненту.
Предварительный этап такого анализа заключается в выявлении структуры изучаемых временных рядов. Если на этом этапе было выявлено, что временные ряды содержат сезонные или циклические колебания, то перед проведением дальнейшего исследования взаимосвязи необходимо устранить сезонную или циклическую компоненту из уровней каждого ряда, поскольку ее наличие приведет к завышению истинных показателей силы и тесноты связи изучаемых временных рядов в случае, если оба ряда содержит циклические колебания одинаковой периодичности, либо к занижению этих показателей в случае, если сезонные или циклические колебания содержат только один из рядов или периодичность колебаний в рассматриваемых временных рядах различна.
Для того чтобы получить коэффициенты корреляции, характеризующие причинно-следственную связь между изучаемыми рядами, следует избавиться от так называемой ложной корреляции, вызванной наличием тенденции в каждом ряде. Обычно это осуществляется с помощью одного из методов исключения тенденции.
Предположим, что по двум временным рядам 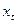 и
и  строится уравнение парной линейной регрессии вида
строится уравнение парной линейной регрессии вида
 = а + b•
= а + b• 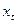
Наличие тенденции в каждом из этих временных рядов означает, что на зависимую  и независимую
и независимую 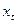 переменные модели оказывает воздействие фактор времени, который непосредственно в модели не учтен.
переменные модели оказывает воздействие фактор времени, который непосредственно в модели не учтен.
6. ДИНАМИЧЕСКИЕ ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ
В эконометрике к числу динамических относятся не все модели, построенные по временным рядам данных. Термин «динамический» характеризует каждый момент времени  в отдельности, а не весь период, для которого строится модель. Эконометрическая модель является динамической, если в данный момент времени
в отдельности, а не весь период, для которого строится модель. Эконометрическая модель является динамической, если в данный момент времени  она учитывает значения входящих в нее переменных, относящиеся как к текущему, так и к предыдущим моментам времени, т. е. если эта модель отражает динамику исследуемых переменных в каждый момент времени.
она учитывает значения входящих в нее переменных, относящиеся как к текущему, так и к предыдущим моментам времени, т. е. если эта модель отражает динамику исследуемых переменных в каждый момент времени.
Можно выделить два основных типа динамических эконометрических моделей. К моделям первого типа относятся модели авторегрессии и модели с распределенным лагом, в которых значения переменной за прошлые периоды времени непосредственно включены в модель. Модели второго типа учитывают динамическую информацию в неявном виде. В эти модели включены переменные, характеризующие ожидаемый или желаемый уровень результата, или одного из факторов в момент времени  . Этот уровень считается неизвестным и определяется экономическими единицами с учетом информации, которой они располагают в момент (
. Этот уровень считается неизвестным и определяется экономическими единицами с учетом информации, которой они располагают в момент (  - 1).
- 1).
В зависимости от способа определения ожидаемых значений показателей различают модели неполной корректировки, адаптивных ожиданий и рациональных ожиданий. Оценка параметров этих моделей сводится к оценке параметров моделей авторегрессии.
При исследовании экономических процессов необходимо моделировать ситуации, когда значение результативного признака в текущий момент времени  формируется под воздействием ряда факторов, действовавших в прошлые моменты времени
формируется под воздействием ряда факторов, действовавших в прошлые моменты времени  Например, на выручку от реализации или прибыль компании текущего периода могут оказывать влияние расходы на рекламу или проведение маркетинговых исследований, сделанные компанией в предшествующие моменты времени. Величину l, характеризующую запаздывание воздействия фактора на результат, называют в эконометрике лагом, а временные ряды самих факторных переменных, сдвинутые на один или более моментов времени, - лаговыми переменными.
Например, на выручку от реализации или прибыль компании текущего периода могут оказывать влияние расходы на рекламу или проведение маркетинговых исследований, сделанные компанией в предшествующие моменты времени. Величину l, характеризующую запаздывание воздействия фактора на результат, называют в эконометрике лагом, а временные ряды самих факторных переменных, сдвинутые на один или более моментов времени, - лаговыми переменными.
Эконометрическое моделирование охарактеризованных процессов осуществляется с применением моделей, содержащих не только текущие, но и лаговые значения факторных переменных. Эти модели называются моделями с распределенным лагом. Модель вида

является примером модели с распределенным лагом.
Наряду с лаговыми значениями независимых, или факторных, переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые моменты или периоды времени. Например, потребление в момент времени  формируется под воздействием дохода текущего и предыдущего периодов, а также объема потребления прошлых периодов, например потребления в период (
формируется под воздействием дохода текущего и предыдущего периодов, а также объема потребления прошлых периодов, например потребления в период (  - 1). Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии. Модель вида
- 1). Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии. Модель вида
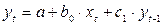
относится к моделям авторегрессии.
Рассмотрим модель с распределенным лагом в ее общем виде в предложении, что максимальная величина лага конечна:
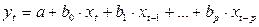
Если в некоторый момент времени  происходит изменение независимой переменной х, то это изменение будет влиять на значения переменной у в течение следующих моментов времени.
происходит изменение независимой переменной х, то это изменение будет влиять на значения переменной у в течение следующих моментов времени.
Коэффициент регрессии 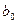 при переменной
при переменной  характеризует среднее абсолютное изменение
характеризует среднее абсолютное изменение  при изменении
при изменении  на 1 ед. своего измерения в некоторый фиксированный момент времени
на 1 ед. своего измерения в некоторый фиксированный момент времени  учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.
учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.
В момент  совокупное воздействие факторной переменной
совокупное воздействие факторной переменной  на результат
на результат  составит
составит 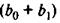 усл. ед., в момент (
усл. ед., в момент (  +2) это воздействие можно охарактеризовать суммой
+2) это воздействие можно охарактеризовать суммой  и т. д. Полученные таким образом суммы называют промежуточными мультипликаторами.
и т. д. Полученные таким образом суммы называют промежуточными мультипликаторами.
С учетом конечной величины лага можно сказать, что изменение переменной  в момент
в момент  на 1 усл. ед. приведет к общему изменению результата через l моментов времени на
на 1 усл. ед. приведет к общему изменению результата через l моментов времени на  абсолютных единиц.
абсолютных единиц.
Введем следующее обозначение:

Величину  называют долгосрочным мультипликатором. Он показывает абсолютное изменение в долгосрочном периоде
называют долгосрочным мультипликатором. Он показывает абсолютное изменение в долгосрочном периоде 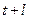 результата у под влиянием изменения на 1 ед. фактора х.
результата у под влиянием изменения на 1 ед. фактора х.
Пример. Интерпретация параметров модели с распределенным лагом.
По результатам изучения зависимости объемов продаж компании в среднем за месяц от расходов на рекламу была получена следующая модель с распределенным лагом (млн. руб. ):

В этой модели краткосрочный мультипликатор равен 4, 5. Это означает, что увеличение расходов на рекламу на 1 млн. руб. ведет в среднем к росту объема продаж компании на 4, 5 млн. руб. в том же периоде. Под влиянием увеличения расходов на рекламу объем продаж компании возрастет в момент времени  на 1 млн. руб.,
на 1 млн. руб.,  - на 4, 5+ 3, 0 = 7, 5 млн. руб.,
- на 4, 5+ 3, 0 = 7, 5 млн. руб.,  - на 7, 5 + 1, 5 = 9, 0 млн. руб. Наконец, долгосрочный мультипликатор для данной модели составит:
- на 7, 5 + 1, 5 = 9, 0 млн. руб. Наконец, долгосрочный мультипликатор для данной модели составит:  = 4, 5 + 3, 0 + 1, 5 + 0, 5 = 9, 5.
= 4, 5 + 3, 0 + 1, 5 + 0, 5 = 9, 5.
В долгосрочной перспективе (например, через 3 месяца) увеличение расходов на рекламу на 1 млн. руб. в настоящий момент времени приведет к общему росту объема продаж на 9, 5 млн. руб.
Применение обычного МНК к таким моделям в большинстве случаев затруднительно по следующим причинам.
Во-первых, текущие и лаговые значения независимой переменной, как правило, тесно связаны друг с другом. Тем самым оценка параметров модели проводится в условиях высокой мультиколлинеарности факторов.
Во-вторых, при большой величине лага снижается число наблюдений, по которому строится модель, и увеличивается число ее факторных признаков. Это ведет к потере числа степеней свободы в модели.
В-третьих, в моделях с распределенным лагом часто возникает проблема автокорреляции остатков. Вышеуказанные обстоятельства приводят к значительной неопределенности относительно оценок параметров модели, снижению их точности и получению неэффективных оценок. Чистое влияние факторов на результат в таких условиях выявить невозможно. Поэтому на Практике параметры моделей с распределенным лагом проводят в предположении определенных ограничений на коэффициенты регрессии и в условиях выбранной структуры лага.
7. КОЭФФИЦИЕНТ КОРРЕЛИЦИИ
Понятие " зависимости" случайных величин, которым пользуются в теории вероятностей, несколько отличается от обычного понятия " зависимости" величин, которым пользуются в математике. Так, математик под " зависимостью" подразумевает только один тип зависимости - полную, жесткую, так называемую функциональную зависимость. Две величины Х и Y называются функционально зависимыми, если, зная значение одного из них, можно точно определить значение другой.
В теории вероятностей встречаются несколько с иным типом зависимости - вероятностной зависимостью. Если величина Y связана с величиной Х вероятностной зависимостью, то, зная значение Х, нельзя точно указать значение Y, а можно указать её закон распределения, зависящий от того, какое значение приняла величина Х.
Вероятностная зависимость может быть более или менее тесной; по мере увеличения тесноты вероятностной зависимости она все более приближается к функциональной. Т. о., функциональную зависимость можно рассматривать как крайний, предельный случай наиболее тесной вероятностной зависимости. Другой крайний случай - полная независимость случайных величин. Между этими двумя крайними случаями лежат все градации вероятностной зависимости - от самой сильной до самой слабой.
Вероятностная зависимость между случайными величинами часто встречается на практике. Если случайные величины Х и Y находятся в вероятностной зависимости, то это не означает, что с изменением величины Х величина Y изменяется вполне определенным образом; это лишь означает, что с изменением величины Х величина Y имеет тенденцию также изменяться (возрастать или убывать при возрастании Х). Эта тенденция соблюдается лишь в общих чертах, а в каждом отдельном случае возможны отступления от неё.
Рассмотрим случайную величину Х, имеющую возможные значения Х1, Х2, ... , Хn с вероятностями р1, р2, ... , рn. нам требуется охарактеризовать каким-то числом положение значений случайной величины на оси абсцисс с учетом того, что эти значения имеют различные значения. Для этой цели обычно пользуются так называемым " средним взвешенным" из значений Хi, причем каждое значение Хi при осреднении должно учитываться с " весом", пропорциональным вероятности этого значения. Таким образом, если обозначить " среднее взвешенное" через М[X] или mx, получим

или, учитывая, что 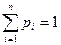 , то
, то
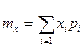
 .
.
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.
Для непрерывной величины Х математическое ожидание, естественно, выражается не суммой, а интегралом:
 ,
,
где  - плотность распределения величины Х.
- плотность распределения величины Х.
Коэффициент корреляции характеризует не всякую зависимость, а только так называемую линейную зависимость. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или же убывать) по линейному закону. Т. о., коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами.
Для определения коэффициента корреляции имеется несколько методов. Однако мы приведем пример с использованием коэффициента корреляции смешанных моментов Пирсона, где

| x | Y | x' | y' | x'y' | x'2 | y'2 | ||||
| 69, 8 | 17, 1 | 1, 9 | 1, 65 | 3, 135 | 3, 61 | 2, 7225 | ||||
| 69, 5 | 16, 9 | 1, 6 | 1, 45 | 2, 32 | 2, 56 | 2, 1025 | ||||
| 68, 8 | 16, 2 | 0, 9 | 0, 75 | 0, 675 | 0, 81 | 0, 5625 | ||||
| 67, 5 | 14, 8 | -0, 4 | -0, 65 | 0, 26 | 0, 16 | 0, 4225 | ||||
| 66, 4 | 14, 1 | -1, 5 | -1, 35 | 2, 025 | 2, 25 | 1, 8225 | ||||
| 65, 5 | 13, 6 | -2, 4 | -1, 85 | 5, 76 | 5, 76 | 3, 4225 | ||||
| ∑ =679 | ∑ =154, 5 | ∑ =12, 855 | ∑ =15, 15 | ∑ =11
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|

