 |
Задания на практические занятия по дисциплине Эконометрика
|
|
|
|
Задания на практические занятия по дисциплине Эконометрика
Согласно нормативу (2 часа практических занятий = 1 задача) за время проведения практических занятий со студентами необходимо решить 10 задач.
При рассмотрении однотипных задач решение прилагается только к одной из них.
Задача 1.
Провести корреляционно регрессионный анализ в зависимости выплаты труда от производительности труда для этого:
1. Построить поле корреляции и выбрать модель уравнения.
2. рассчитать парам. уравнения построить уравнение Тренда
3. Рассчитать выровненное значение результативного признака
4. Рассчитать среднюю ошибку аппроксимации, сделать выводы.
5. Определить тесноту связи между изученными признаками.
6. Рассчитать коэффициент детерминации и эластичности.
| № | y | х | yx | y | x | yx | y-y | A |
| 23, 6 | 556, 96 | 24, 96 | -1, 36 | 5, 77 | ||||
| 31, 6 | 2496, 4 | 998, 56 | 28, 02 | 3, 58 | 11, 33 | |||
| 35, 2 | 3203, 2 | 32, 1 | 3, 1 | 8, 81 | ||||
| 27, 1 | 2547, 4 | 734, 41 | 33, 12 | -6, 02 | 22, 21 | |||
| 23, 6 | 1699, 2 | 556, 96 | 25, 64 | -2, 04 | 4, 45 | |||
| 25, 7 | 2081, 7 | 660, 49 | 28, 7 | -3 | 11, 67 | |||
| 38, 2 | 3667, 2 | 1459, 2 | 33, 8 | 4, 4 | 11, 52 | |||
| 17, 8 | 316, 84 | 16, 46 | 1, 34 | 7, 53 | ||||
| итог | 222, 8 | 18148, 1 | 6522, 5 | 222, 8 | 83, 29 | |||
| ср. зн | 27, 85 | 78, 5 | 2268, 51 | 815, 31 | 6405, 5 |
|
|
|
|
| 6, 3 | 15, 59 |
|
|
|
|
|
|
|
| 39, 69 | 243, 25 |
|
|
|
|
|
|
2. Рассчитаем параметры уравнения a и b и построим уравнение Тренда
yx = a + b * x
yx – yx
b = ------------
x
2268. 51 – 27. 85 * 78. 5
b = ----------------------------- = 0. 34
(15. 59)
= 815. 31 – (27. 85) = 39. 69
= 39. 69 = 6. 3
= 6405. 5 – (78. 5) = 243. 25
= 243. 25 = 15. 59
a = 27. 85 – 0. 34 * 78. 25 = 1. 16
Уравнение Тренда
yx = a + b * x = 1. 16 + 0. 34 * x
Вывод: С увеличением оплаты труда на 1 рубль, уровень производительности труда увеличивается в среднем на 0, 34%
|
|
|
3. Рассчитаем выраженные значения результативного признака.
Для этого в уравнение Тренда подставим соответствующие значения факторного признака х.
Yx1 = 1. 16 + 0. 34 * 70 = 24. 96
Yx2 = 1. 16 + 0. 34 * 79 = 28. 02
Yx3 = 1. 16 + 0. 34 * 91 = 32. 1
Yx4 = 1. 16 + 0. 34 * 94 = 33. 12
Yx5 = 1. 16 + 0. 34 * 72 = 25. 64
Yx6 = 1. 16 + 0. 34 * 81 = 28. 7
Yx7 = 1. 16 + 0. 34 * 96 = 33. 8
Yx8 = 1. 16 + 0. 34 * 45 = 16. 46
рассчитаем среднюю ошибку аппроксимации
y - yx
A = --------------- * 100 и подставим в таблицу
Y
найдем величину средней ошибки аппроксимации (А)
27, 1
A = ---------- = 3, 39%
4. Рассчитаем коэффициент корреляции.
15, 59
= 0, 34 * ----------- = 0, 84
6, 3
Вывод: Связь сильная, с ростом заработной платы рабочего производительность труда увеличивается.
5. Определить коэффициент детерминации.
= (0, 84) * 100% = 70, 56
Вывод: Вариация производительности труда на 70, 56 объясняется вариацией производительности труда на одного рабочего. Оплата труда на 70, 56% зависит от производительности труда.
Определить коэффициент эластичности.
b * x 78, 5
Ə = --------- = 0, 34 ---------- = 0, 96
Y 27, 85
Вывод: Производительность труда на 0, 96% зависит от средней заработной платы одного рабочего.
Задача 2.
Имеются данные за 12 месяцев года по району города о рынке вторичного жилья (y – стоимость квартиры (тыс. у. е. ), x – размер общей площади (м2)). Данные приведены в табл. 1. 4.
Таблица 1
| Месяц | ||||||||||||
| у | 22, 5 | 25, 8 | 20, 8 | 15, 2 | 25, 8 | 19, 4 | 18, 2 | 21, 0 | 16, 4 | 23, 5 | 18, 8 | 17, 5 |
| х | 29, 0 | 36, 2 | 28, 9 | 32, 4 | 49, 7 | 38, 1 | 30, 0 | 32, 6 | 27, 5 | 39, 0 | 27, 5 | 31, 2 |
Задание:
1. Рассчитайте параметры уравнений регрессий
 и
и  .
.
2. Оцените тесноту связи с показателем корреляции и детерминации.
3. Рассчитайте средний коэффициент эластичности и дайте сравнительную оценку силы связи фактора с результатом.
4. Рассчитайте среднюю ошибку аппроксимации и оцените качество модели.
|
|
|
5. С помощью F-статистики Фишера (при 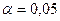 ) оцените надежность уравнения регрессии.
) оцените надежность уравнения регрессии.
6. Рассчитайте прогнозное значение  , если прогнозное значение фактора увеличится на 5% от его среднего значения. Определите доверительный интервал прогноза для
, если прогнозное значение фактора увеличится на 5% от его среднего значения. Определите доверительный интервал прогноза для  .
.
7. Расчеты должны быть подробны, как показано в примере 1, и сопровождены пояснениями.
Решение
Составим таблицу расчетов 2.
Все расчеты в таблице велись по формулам
 .
.
Таблица 2
|
| х | х2 | у | ху | у2 | 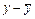
| 
| 
| 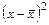
| 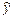
| 
| 
| А(%) |
| 29, 0 | 841, 0 | 22, 5 | 652, 5 | 506, 3 | 2, 1 | -4, 5 | 4, 38 | 20, 33 | 18, 93 | 3, 57 | 12, 75 | 15, 871 | |
| 36, 2 | 1310, 4 | 25, 8 | 934, 0 | 665, 6 | 5, 4 | 2, 7 | 29, 07 | 7, 25 | 21, 28 | 4, 52 | 20, 40 | 17, 506 | |
| 28, 9 | 835, 2 | 20, 8 | 601, 1 | 432, 6 | 0, 4 | -4, 6 | 0, 15 | 21, 24 | 18, 90 | 1, 90 | 3, 62 | 9, 152 | |
| 32, 4 | 1049, 8 | 15, 2 | 492, 5 | 231, 0 | -5, 2 | -1, 1 | 27, 13 | 1, 23 | 20, 04 | -4, 84 | 23, 43 | 31, 847 | |
| 49, 7 | 2470, 1 | 25, 8 | 1282, 3 | 665, 6 | 5, 4 | 16, 2 | 29, 07 | 262, 17 | 25, 70 | 0, 10 | 0, 01 | 0, 396 | |
| 38, 1 | 1451, 6 | 19, 4 | 739, 1 | 376, 4 | -1, 0 | 4, 6 | 1, 02 | 21, 08 | 21, 90 | -2, 50 | 6, 27 | 12, 911 | |
| 30, 0 | 900, 0 | 18, 2 | 546, 0 | 331, 2 | -2, 2 | -3, 5 | 4, 88 | 12, 31 | 19, 26 | -1, 06 | 1, 12 | 5, 802 | |
| 32, 6 | 1062, 8 | 21, 0 | 684, 6 | 441, 0 | 0, 6 | -0, 9 | 0, 35 | 0, 83 | 20, 11 | 0, 89 | 0, 80 | 4, 256 | |
| 27, 5 | 756, 3 | 16, 4 | 451, 0 | 269, 0 | -4, 0 | -6, 0 | 16, 07 | 36, 10 | 18, 44 | -2, 04 | 4, 16 | 12, 430 | |
| 39, 0 | 1521, 0 | 23, 5 | 916, 5 | 552, 3 | 3, 1 | 5, 5 | 9, 56 | 30, 16 | 22, 20 | 1, 30 | 1, 69 | 5, 536 | |
| 27, 5 | 756, 3 | 18, 8 | 517, 0 | 353, 4 | -1, 6 | -6, 0 | 2, 59 | 36, 10 | 18, 44 | 0, 36 | 0, 13 | 1, 923 | |
| 31, 2 | 973, 4 | 17, 5 | 546, 0 | 306, 3 | -2, 9 | -2, 3 | 8, 46 | 5, 33 | 19, 65 | -2, 15 | 4, 62 | 12, 277 | |
| 402, 1 | 13927, 8 | 244, 9 | 8362, 6 | 5130, 7 | 0, 0 | 0, 0 | 132, 7 | 454, 1 | - | - | 79, 0 | 129, 9 |
| Среднее значение | 33, 5 | 1160, 7 | 20, 4 | 696, 9 | 427, 6 | - | - | - | - | - | - | 6, 6 | 10, 8 |
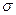
| 6, 43 | - | 3, 47 | - | - |
| |||||||

| 41, 28 | - | 12, 06 | - | - |
| |||||||
Тогда
 ,
,

и линейное уравнение регрессии примет вид: 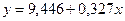 .
.
Рассчитаем коэффициент корреляции:
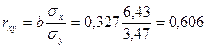 .
.
Связь между признаком  и фактором
и фактором  заметная.
заметная.
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
R2 = 0, 6062 = 0, 367
Средний коэффициент эластичности  позволяет проверить, имеют ли экономический смысл коэффициенты модели регрессии.
позволяет проверить, имеют ли экономический смысл коэффициенты модели регрессии.
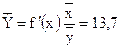
Для оценки качества модели определяется средняя ошибка аппроксимации:
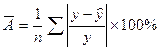 ,
,
допустимые значения которой 8 - 10 %.
|
|
|
Вычислим значение  -критерия Фишера.
-критерия Фишера.
 ,
,
где
 – число параметров уравнения регрессии (число коэффициентов при объясняющей переменной
– число параметров уравнения регрессии (число коэффициентов при объясняющей переменной  );
);
 – объем совокупности.
– объем совокупности.
 .
.
По таблице распределения Фишера находим
 .
.
Так как  , то гипотеза
, то гипотеза  о статистической незначимости параметра
о статистической незначимости параметра 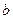 уравнения регрессии отклоняется.
уравнения регрессии отклоняется.
Так как  , то можно сказать, что 36, 7% результата объясняется вариацией объясняющей переменной.
, то можно сказать, что 36, 7% результата объясняется вариацией объясняющей переменной.
Выберем в качестве модели уравнения регрессии  , предварительно линеаризовав модель. Введем обозначения:
, предварительно линеаризовав модель. Введем обозначения:  . Получим линейную модель регрессии
. Получим линейную модель регрессии 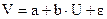 .
.
Рассчитаем коэффициенты модели, поместив все промежуточные расчеты в табл. 3.
|
|
|


