Таблица 3. Рассчитаем параметры уравнения:

Таблица 3

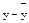
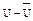
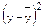
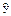
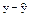
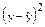
			y	yU	y2								А(%)
	5, 385	29, 0	22, 5	121, 17	506, 25	1, 640	-0, 452	2, 69	0, 20	13, 74	8, 76	76, 7	38, 92
	6, 017	36, 2	25, 8	155, 23	665, 64	4, 940	0, 180	24, 40	0, 03	14, 01	11, 79	139, 0	45, 70
	5, 376	28, 9	20, 8	111, 82	432, 64	-0, 060	-0, 461	0, 004	0, 21	13, 74	7, 06	49, 9	33, 95
	5, 692	32, 4	15, 2	86, 52	231, 04	-5, 660	-0, 145	32, 04	0, 02	13, 87	1, 33	1, 8	8, 72
	7, 050	49, 7	25, 8	181, 89	665, 64	4, 940	1, 213	24, 40	1, 47	14, 42	11, 38	129, 5	44, 11
	6, 173	38, 1	19, 4	119, 75	376, 36	-1, 460	0, 336	2, 13	0, 11	14, 07	5, 33	28, 4	27, 45
	5, 477	30, 0	18, 2	99, 69	331, 24	-2, 660	-0, 360	7, 08	0, 13	13, 78	4, 42	19, 5	24, 27
	5, 710	32, 6	21, 0	119, 90		0, 140	-0, 127	0, 02	0, 02	13, 88	7, 12	50, 7	33, 89
	5, 244	27, 5	16, 4	86, 00	268, 96	-4, 460	-0, 593	19, 89	0, 35	13, 68	2, 72	7, 4	16, 58
	6, 245	39, 0	23, 5	146, 76	552, 25	2, 640	0, 408	6, 97	0, 17	14, 10	9, 40	88, 3	39, 98
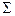
	58, 368	343, 4	208, 600	1228, 71	4471, 02	-	-	-	-	-	-	-	313, 567
Среднее значение	5, 837	34, 34	20, 860	122, 871	447, 10	-	-	-	-	-	-	-	31, 357
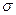
	0, 549	-	3, 646	-	-	-	-
	0, 302	-	13, 292	-	-	-	-

Рассчитаем параметры уравнения:

,

,

.

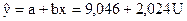
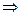
Коэффициент корреляции

.

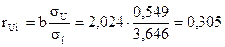Коэффициент детерминации

,

следовательно, только 9, 3% результата объясняется вариацией объясняющей переменной .

 

,

,

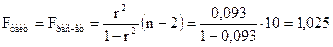следовательно, гипотеза о статистической незначимости уравнения регрессии принимается. По всем расчетам линейная модель надежнее, и последующие расчеты мы сделаем для нее.

Оценим значимость каждого параметра уравнения регрессии

.

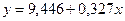Используем для этого t-распределение (Стьюдента). Выдвигаем гипотезу о статистической незначимости параметров, т. е.

.

.

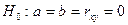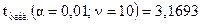Определим ошибки .

,

,

,

,

,

.

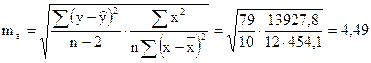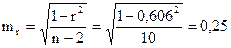Полученные оценки модели и ее параметров позволяют использовать ее для прогноза.

Рассчитаем

.

Тогда

.

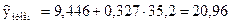Средняя ошибка прогноза

,

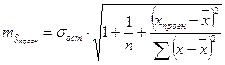где

,

.

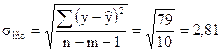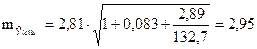Строим доверительный интервал с заданной доверительной вероятностью :

 

,

,

.

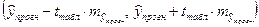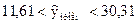Найденный интервальный прогноз достаточно надежен (доверительная вероятность 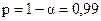) и достаточно точен, т. к. .

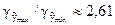Оценим значимость каждого параметра уравнения регрессии

.

Используем для этого t-распределение (Стьюдента). Выдвигаем гипотезу о статистической незначимости параметров, т. е.

.

.

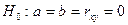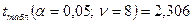Определим ошибки .

,

,

, ,

, .

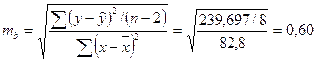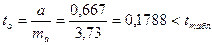Следователь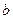но, и не случайно отличаются от нуля, а сформировались под влиянием систематически действующей производной.

1. 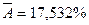, следовательно, качество модели не очень хорошее.

2. Полученные оценки модели и ее параметров позволяют использовать ее для прогноза.

Рассчитаем 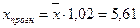. Тогда .

3. Средняя ошибка прогноза

,

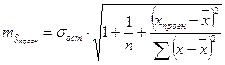где

,

.

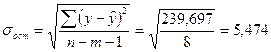Строим доверительный интервал с заданной доверительной вероятностью :

,

,

.

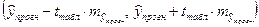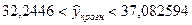Найденный интервальный прогноз достаточно надежен (доверительная вероятность 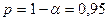) и достаточно точен, т. к. .

 

Задача 3.

Имеются данные о деятельности крупнейших компаний в течение двенадцати месяцев 199Х года. Данные приведены в табл. 4.

Известны – чистый доход (у), оборот капитала (х₁), использованный капитал (х₂) в млрд у. е.

Таблица 4

у	х1	х2
1, 5	5, 9	5, 9
5, 5	53, 1	27, 1
2, 4	18, 8	11, 2
3, 0	35, 3	16, 4
4, 2	71, 9	32, 5
2, 7	93, 6	25, 4
1, 6	10, 0	6, 4
2, 4	31, 5	12, 5
3, 3	36, 7	14, 3
1, 8	13, 8	6, 5
2, 4	64, 8	22, 7
1, 6	30, 4	15, 8

Задание:

1. Рассчитайте параметры линейного уравнения множественной регрессии.

2. Дайте оценку силы связи факторов с результатом с помощью средних коэффициентов эластичности.

3. Оцените статистическую зависимость параметров и уравнения регрессии в целом с помощью соответственно критериев Стьюдента и Фишера (α =0, 01).

4. Рассчитайте среднюю ошибку аппроксимации. Сделайте вывод.

5. Составьте матрицы парных и частных коэффициентов корреляции и укажите информативные факторы.

6. Оцените полученные результаты, выводы оформите в аналитической записке.

Решение

Результаты расчетов приведены в табл. 5.

Таблица 5

	y	x1	x2	yx1	yx2	x1x2	x12	x22	y2
	1, 5	5, 9	5, 9	8, 85	8, 85	34, 81	34, 81	34, 81	2, 25
	5, 5	53, 1	27, 1	292, 05	149, 05	1439, 01	2819, 61	734, 41	30, 25
	2, 4	18, 8	11, 2	45, 12	26, 88	210, 56	353, 44	125, 44	5, 76
		35, 3	16, 4	105, 90	49, 20	578, 92	1246, 09	268, 96
	4, 2	71, 9	32, 5	301, 98	136, 50	2336, 75	5169, 61	1056, 25	17, 64
	2, 7	93, 6	25, 4	252, 72	68, 58	2377, 44	8760, 96	645, 16	7, 29
	1, 6		6, 4	16, 00	10, 24	64, 00	100, 00	40, 96	2, 56
	2, 4	31, 5	12, 5	75, 60	30, 00	393, 75	992, 25	156, 25	5, 76
	3, 3	36, 7	14, 3	121, 11	47, 19	524, 81	1346, 89	204, 49	10, 89
	1, 8	13, 8	6, 5	24, 84	11, 70	89, 70	190, 44	42, 25	3, 24
	2, 4	64, 8	22, 7	155, 52	54, 48	1470, 96	4199, 04	515, 29	5, 76
	1, 6	30, 4	15, 8	48, 64	25, 28	480, 32	924, 16	249, 64	2, 56
	32, 4	465, 8	196, 7	1448, 33	617, 95	10001, 03	26137, 30	4073, 91	102, 96
Средн.	2, 7	38, 8	16, 4	120, 69	51, 50	833, 42	-	-	65, 80
	1, 2	27, 1	8, 8	-	-	-	-	-	-
	1, 4	732, 4	77, 2	-	-	-	-	-	-

Рассматриваем уравнение вида:

.

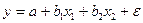Параметры уравнения можно найти из решения системы уравнений:

Или, перейдя к уравнению в стандартизированном масштабе:

 

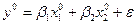, где

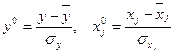– стандартизированные переменные,

– стандартизированные коэффициенты:

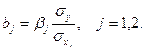
Коэффициенты определяются из системы уравнений:

, ;

;

, ;

, ;

, ;

, ;

, ;

.

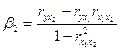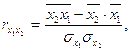
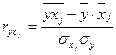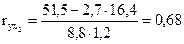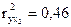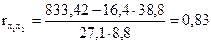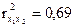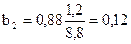Стандартизированная форма уравнения регрессии имеет вид:

.

 

Естественная форма уравнения регрессии имеет вид:

.

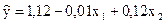Для выяснения относительной силы влияния факторов на результативный признак рассчитываются средние коэффициенты эластичности:

,

,

.

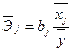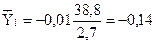Следовательно, при увеличении оборота капитала (x₁) на 1% чистый доход (y) уменьшается на 0, 14% от своего среднего уровня. При повышении использованного капитала на 1% чистый доход повышается на 0, 73% от своего среднего уровня.

Линейные коэффициенты частной корреляции для уравнения определяются следующим образом:

,

.

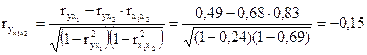Линейный коэффициент множественной корреляции рассчитывается по формуле

 

.

Коэффициент множественной детерминации .

,

где

- объем выборки,

- число факторов модели.

В нашем случае

.

Так как , то 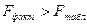и потому уравнение незначимо.

Выясним статистическую значимость каждого фактора в уравнении множественной регрессии.

Для этого рассчитаем частные -статистики.

.

Так как , то и следует вывод о нецелесообразности включения в модель фактора после фактора .

.

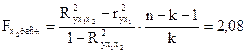Так как 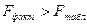, то следует вывод о нецелесообразности включения в модель фактора после фактора .

Результаты расчетов позволяют сделать вывод:

1) о незначимости фактора и нецелесообразности включения его в уравнение регрессии;

2) о незначимости фактора и нецелесообразности включения его в уравнение регрессии.

Задача 4.

1. Используя необходимое и достаточное условие идентификации, определить, идентифицировано ли каждое уравнение модели.

2. Определите тип модели.

3. Определите метод оценки параметров модели.

4. Опишите последовательность действий при использовании указанного метода.

5. Результаты оформите в виде пояснительной записки.

Модель денежного и товарного рынков:

R_t = a₁+b₁₂Y_t+b₁₄M_t+e₁,

Y_t = a₂+b₂₁R_t+ b₂₃I_t+ b₂₅G_t+e₂,

I_t = a₃+b₃₁R_t+e₃,

где

R – процентные ставки;

Y – реальный ВВП;

M – денежная масса;

I – внутренние инвестиции;

G – реальные государственные расходы.

Решение

1. Модель имеет три эндогенные (R_tY_tI_t) и две экзогенные переменные (M_tG_t).

Проверим необходимое условие идентификации:

1-е уравнение: D=1, H=2, D+1=H - уравнение идентифицировано.

2-е уравнение: D=1, H=1, D+1=2 - уравнение сверхидентифицировано.

3-е уравнение: D=1, H=2, D+1=H - уравнение идентифицировано.

Следовательно, необходимое условие идентифицируемости выполнено.

Проверим достаточное условие:

В первом уравнении нет переменных I_t, G_t

Строим матрицу:

	It	Gt
2 ур.	b23	b23
3 ур.

det M = det 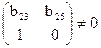, rank M =2.

Во втором уравнении нет переменных M_t

det M ¹ 0

В третьем уравнении нет переменных Y_t, M_t, G_t

Строим матрицу:

det M /

Следовательно, достаточное условие идентифицируемости выполнено.

Система точно идентифицируема.

2. Найдем структурные коэффициенты модели.

Для этого:

Запишем систему в матричной форме, перенеся все эндогенные переменные в левые части системы:

 

R_t-b₁₂Y_t=a₁+b₁₂M_t

Y_t-b₂₁R_t-b₂₃I_t=a₂+b₂₅G_t

I_t-b₃₁R_t=a₃

откуда

, и , , , .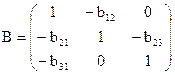

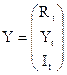Решаем систему относительно 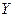: . Найдем

, где –

алгебраические дополнения соответствующих элементов матрицы , 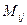– минор, т. е. определитель, полученный из матрицы вычеркиванием i-й строки и j-го столбца.

,

,

,

.

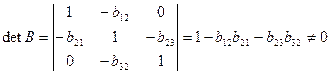Поэтому

 

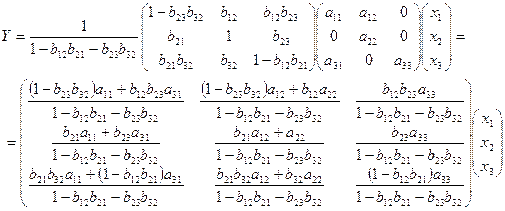
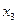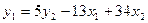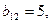
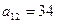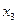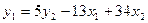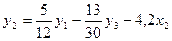В данном случае эти коэффициенты можно найти значительно проще. Находим из второго уравнения приведенной системы и подставим его в первое уравнение этой системы. Тогда первое уравнение системы примет вид: , откуда , . Из третьего уравнения системы находим и подставляем во второе уравнение системы, получим: , решая его совместно с уравнением и, исключая , получим . Сравнивая это уравнение со вторым уравнением системы получим . Выражая из второго уравнения, и подставляя в третье системы (3. 2), получим . Сравнивая это уравнение с третьим уравнением системы, получим .

Задача 5.

Имеются данные за пятнадцать дней по количеству пациентов клиники, прошедших через соответствующие отделения в течение дня. Данные приведены в табл. 6.

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: