 |
Проблема многокритериальности. Метод свёрток, различные виды свёрток, достоинства и недостатки. Примеры. Целевое программирование.
|
|
|
|
Пусть даны
i = 1, 2,…,n
Задача:
Максимизировать выгоды (Benefit) и
минимизировать расходы (Cost).
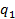и 
– критерии.
Наиболее часто используемым примером при принятии решений многокритериальных задач является использование свертки критериев.
P – прибыль (profit), интегральный критерий.
С позиции СА (в частности ТПР), прибыль – это линейная свертка двух критериев.
Мы строим прямую, которая отсекает убыточные проекты (
). Дальше мы строим параллельную ей прямую, и приходим к выводу, что проект №3 наиболее прибыльный.
Проблема многокритериальности в том, что как правило, не имеет однозначного решения. Этот субъективизм, во-первых, связан с видом интегральной функции, а во-вторых, связан с весами, которые мы придаем отдельным критериям.
Q – рентабельность, интегральный критерий.
Единица особой роли не играет, главное отношение 
.
Рентабельность – это мультипликативная свертка двух критериев.
Мы изменяем угол наклона прямой. Самый большой угол наклона 
у проекта №1, значит он самый рентабельный.
| Линейная свертка (аддитивная свертка) | 
|
| Мультипликативная свертка | 
Однородная функция первой степени
|
– Функция Кобба-Дугласа
Прологарифмируем 
, мы получим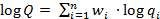 
.
Получается аналог линейной свертки. Мы получили не сам критерий, а какую-то функцию от него. Причем эта функция монотонна.
1. 
2. 
Если 1 и 2 выполняются, то функция монотонна.
Эта схема работает, даже если критерии имеют качественные значения (лучше – хуже, больше – меньше).
– интегральный критерий или суперкритерий.
Еще один вариант функции, которая может использоваться:
Пусть 
Группы критериев
Compand (составной, сложный)
|
|
|
Метрический критерий
– вектор, критерий со значениями
q* – целевое значение.
Эвклидова метрика
Манхэттенская метрика
Целевое программирование (GP)
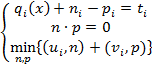
Допустим, у нас есть критерий 
, есть целевое значение 
. Этот критерий может иметь значение либо большее, либо меньшее чем . Если 
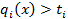, то нужно отнять 
.
Если 
, то нужно прибавить 
. При этом 
. Мы должны найти такую точку, которая минимизирует суммы этих недоборов и переборов с некоторыми весами, т.е.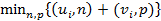 
.
и 
– скалярные произведения.
Оптимальность по Эджворту-Парето, графическая иллюстрация. Необходимость дополнительного критерия. Критерий оптимальности Нэша. Дилемма заключённого, сравнение решений, использующих разные критерии оптимальности.
В экономике широко используется техника, связанная с анализом Парето-эффективности. Оптимальность по Эджворту-Парето – это множество эффективных (доминирующих) решений, которые не улучшаемы одновременно более чем по одному критерию.
Математическая формулировка:
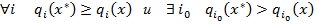
– набор параметров, характеризующий оптимальное по Парето решение.
Определяющим свойством множества Парето является следующее: данная альтернатива хотя бы по одному показателю (критерию) лучше, чем другие.
Выбор на этом множестве возможен с привлечением внешнего дополнительного критерия, который субъективен.
Оптимальность по Парето
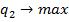
Эти весовые коэффициенты задают некоторую систему предпочтений.
Под критерием могут выступать интересы одного человека или группы людей (actors – действующие лица).
Гиперплоскость
Гиперповерхность
Критерий зрительно (геометрически) означает, что мы выбираем гиперплоскость или гиперповерхность. Если мы выбираем такую гиперповерхность, и оказывается, что она проходит не через одну точку, то нужно еще привлечь дополнительный критерий.
Наша задача – сузить выбор.
|
|
|
|
|
|
