 |
Нахождение обратной матрицы по общей формуле
|
|
|
|
а) Возьмем матрицу второго порядка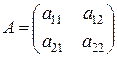 
. Обозначим обратную к ней: 
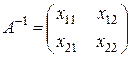. Согласно определению обратной матрицы должно выполняться условие: 
.
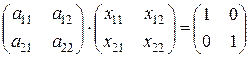Выполнив умножение в левой части и приравнивая соответствующие элементы матриц в левой и правой части, получим две системы для нахождения неизвестных элементов обратной матрицы:
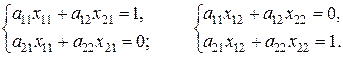
Найдем решения указанных систем:
.
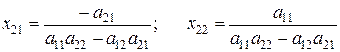Назовем выражение, стоящее в знаменателях формул и составленное из элементов матрицы второго порядка, определителем второго порядка. Определитель кратко обозначается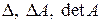 
. Последнее обозначение идет от латинского слова детерминант – определитель. В развернутом виде определитель второго порядка записывают так: 
.
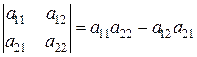Чтобы вычислить определитель второго порядка, нужно из произведения элементов, стоящих на главной диагонали, вычесть произведение элементов, стоящих на побочной диагонали.
Пример.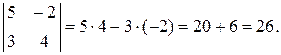 
Если в определителе вычеркнуть строку с номером 
и столбец с номером 
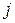, то оставшаяся часть определителя называется минором 
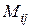. Взятый с определенным знаком минор имеет название алгебраического дополнения: 
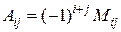. Из этого определения следует, что, если сумма номеров вычеркнутых строки и столбца – четное число, то алгебраическое дополнение совпадает с минором. Если же эта сумма – число нечетное, то алгебраическое дополнение противоположно минору по знаку.
Используя введенные обозначения и вынося за знак матрицы общий множитель всех элементов, формулу обратной матрицы второго порядка можем записать в следующем виде:
.
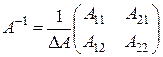б) Рассмотрим матрицу третьего порядка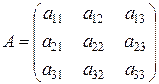 
. Обозначим обратную к ней 
. Согласно определению:
.
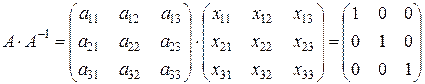Действуя аналогично пункту а), получим 3 системы для нахождения 9 неизвестных элементов обратной матрицы:
|
|
|
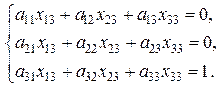
Решая составленные системы и используя введенные обозначения, получим формулу обратной матрицы третьего порядка:
,
где 
- определитель матрицы третьего порядка, записываемый в развёрнутом виде следующим образом:
.
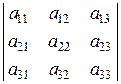Определитель третьего порядка вычисляется по формуле:
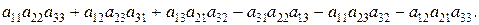
Если формулу для вычисления определителей второго порядка запомнить легко, этого нельзя сказать про формулу для вычисления определителей третьего порядка. Для ее запоминания имеются специальные правила, одно из них – “правило треугольников”.
       
|
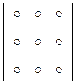
Произведения элементов, стоящих на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали, входят в определитель с тем знаком, который получится при умножении.
       
|
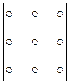
Произведения элементов, стоящих на побочной диагонали и в вершинах треугольников с основаниями, параллельными побочной диагонали, входят в определитель с обратным знаком.
На рисунках элементы определителя обозначены точками.
Пример. Вычислить определитель третьего порядка:
.
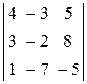Обозначим значение определителя 
и найдем его, используя правило треугольников.
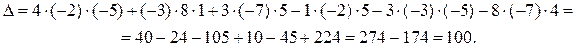
Сравнение двух выведенных формул позволяет, пользуясь индуктивным подходом, написать формулу обратной матрицы для квадратной матрицы произвольного порядка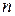 
:
.
Из полученной формулы следует, что обратную матрицу можно найти только для невырожденных матриц, т.е. таких, у которых определитель не равен 0.
Для того, чтобы составить обратную матрицу, необходимо:
1) вычислить определитель матрицы;
2) если определитель отличен от 0, то найти алгебраические дополнения всех элементов;
3) поставив алгебраические дополнения на место элементов, составить матрицу и транспонировать ее;
4) разделить элементы транспонированной матрицы из алгебраических дополнений на величину определителя (если элементы матрицы не делятся нацело на определитель, то деление записывают в виде множителя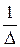 
перед матрицей).
|
|
|
Пример. Найти матрицу, обратную матрице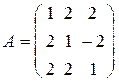 
.
1) Вычислим определитель 
.
2) Найдем алгебраические дополнения элементов матрицы:
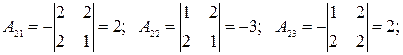
3) Составим матрицу из алгебраических дополнений 
:
.
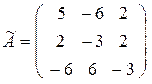и транспонируем ее:
.
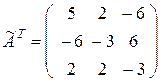3) Выпишем обратную матрицу:
.
Для проверки найдем произведение 
:
|
|
|
