 |
Решение систем с помощью обратной матрицы (матричный способ)
|
|
|
|
Способ основан на том, что любую систему линейных уравнений можно записать в матричном виде: 
, где 
– матрица из коэффициентов при неизвестных, 
– матрица-столбец из самих неизвестных, 
– матрица-столбец из свободных членов уравнений.
Рассмотрим для примера систему 
. Введем матрицы 
, 
, 
. С помощью этих матриц систему можно записать так: 
. Выполнив действие в левой части равенства и используя условие равенства матриц, придем снова к исходной системе. В матричном виде можно представить и прямоугольные системы, например, систему 
можно записать так: 
.
Итак, всякую систему можно записать в виде матричного уравнения . Если матрица в этом уравнении квадратная, то его можно решить по соответствующей формуле: 
.
Пример. Систему линейных уравнений 
решить с помощью обратной матрицы.
Выпишем матрицу коэффициентов системы 
и найдем для неё обратную по общей формуле: 
. Тогда 
. Таким образом, 
. Подстановкой найденных значений во все уравнения системы убеждаемся, что оно верное.
Решение систем по формулам Крамера
Для квадратной неоднородной системы с любым числом уравнений 
неизвестную величину с номером 
можно найти по формуле:
где 
– главный определитель системы;
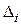– вспомогательный определитель, полученный из главного заменой коэффициентов при неизвестном 
на столбец свободных членов.
Анализ полученной формулы и применение ее на практике для решения систем позволяет сделать следующие выводы:
1) если главный определитель системы 
, то система имеет единственное решение;
2) если 
, а хотя бы один из вспомогательных определителей 
, то система не имеет решения;
3) если и главный и все вспомогательные определители равны 0, то система или не имеет решения, или имеет бесконечное множество решений.
|
|
|
Формулы Крамера являются особенно удобными, когда коэффициенты системы не являются целыми числами.
Пример. Систему линейных уравнений 
решить по формулам Крамера.
Вычислим необходимые определители:
Тогда 
.
Примечание: формула и пример вычисления определителя второго порядка приведены на стр. 10.
Пример решения контрольной работы №1
Задание 1
Вычислить значение функции 
, если
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Решение
Подставим значение 
в данную функцию. Выполним действия в числителе и знаменателе полученной функции, предварительно вычислив
.
Получим 
.
Чтобы выполнить деление комплексных чисел, помножим числитель и знаменатель на выражение, сопряженное знаменателю, то есть на (11+3 i), получим
.
Назовем число 
. Изобразим его на комплексной плоскости:
Тригонометрическая форма комплексного числа имеет вид:
,
где 
– модуль комплексного числа и 
– главное значение аргумента комплексного числа, его можно найти, как рассказано в пункте 1.1.1.
Для полученного комплексного числа 
,, 
, 
. Тогда число 
в тригонометрической форме для нашего примера будет иметь вид: 
.
Ответ: 
.
Задание 2
Найти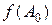 
, если 
.
Решение
Запишем 
, где 
– единичная матрица. Найдем 
, определим выражение в скобке: 
.
Окончательно: 
.
Задание 3
Найти решение системы линейных алгебраических уравнений
по формулам Крамера.
Для данной системы формулы Крамера имеют вид:
.
Вычислим необходимые определители, используя правило треугольников (см. стр. 11, 12):
Тогда: 
Подстановкой в систему убеждаемся, что решение верное.
Ответ: 
.
Задание 4
Пример решения этого задания приведён на страницах 15,16.
Задания контрольной работы №1
Вариант 1
Задание 1
Вычислить значение функции , если
|
|
|
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти 
, если 
.
Задание 3
Найти решение системы линейных алгебраических уравнений
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
методом Гаусса.
Вариант 2
Задание 1
Вычислить значение функции , если
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти , если 
.
Задание 3
Найти решение системы линейных алгебраических уравнений
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
методом Гаусса.
Вариант 3
Задание 1
Вычислить значение функции , если
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти , если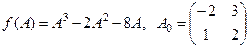 
.
Задание 3
Найти решение системы линейных алгебраических уравнений
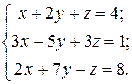
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
методом Гаусса.
Вариант 4
Задание 1
Вычислить значение функции , если
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти , если 
.
Задание 3
Найти решение системы линейных алгебраических уравнений
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
методом Гаусса.
Вариант 5
Задание 1
Вычислить значение функции , если
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти , если 
.
Задание 3
Найти решение системы линейных алгебраических уравнений
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
методом Гаусса.
Вариант 6
Задание 1
Вычислить значение функции , если
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти , если 
.
Задание 3
Найти решение системы линейных алгебраических уравнений
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
|
|
|
методом Гаусса.
Вариант 7
Задание 1
Вычислить значение функции , если
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти , если 
.
Задание 3
Найти решение системы линейных алгебраических уравнений
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
методом Гаусса.
Вариант 8
Задание 1
Вычислить значение функции , если
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти , если 
.
Задание 3
Найти решение системы линейных алгебраических уравнений
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
методом Гаусса.
Вариант 9
Задание 1
Вычислить значение функции , если
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти , если 
.
Задание 3
Найти решение системы линейных алгебраических уравнений
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
методом Гаусса.
Вариант 10
Задание 1
Вычислить значение функции , если
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти , если 
.
Задание 3
Найти решение системы линейных алгебраических уравнений
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
методом Гаусса.
|
|
|
