 |
Уравнение прямой в отрезках
|
|
|
|
Если в общем уравнении прямой  , то перенося свободный член С в правую часть уравнения и разделив все его члены на (– С), получим уравнение вида
, то перенося свободный член С в правую часть уравнения и разделив все его члены на (– С), получим уравнение вида
 ,
,
где a, b – отрезки, отсекаемые прямой на осях координат,  ,
, 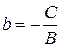 .
.
 Уравнение прямой с угловым коэффициентом
Уравнение прямой с угловым коэффициентом
Пусть прямая l, проходящая через точку 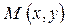 , составляет угол j (
, составляет угол j ( ) с осью Ox и пересекает ось Oy в точке
) с осью Ox и пересекает ось Oy в точке 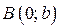 (см. рис.).
(см. рис.).
Из треугольника BMK находим
 ,
,
откуда, обозначив  (угловой коэффициент), получим
(угловой коэффициент), получим
 ,
,
или  .
.
Угол между двумя прямыми
Угол определяется по следующим формулам.
Если уравнения прямых заданы в виде
 ,
,
то  .
.
Если уравнения прямых даны в общем виде
 ,
,
то  .
.
Расстояние от точки до прямой
Рассмотрим прямую l, заданную общим уравнением  , где
, где 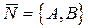 – нормальный вектор прямой. Найдем расстояние d от точки
– нормальный вектор прямой. Найдем расстояние d от точки  до прямой l.
до прямой l.
Под расстоянием от точки до прямой понимается длина отрезка перпендикуляра, опущенного из этой точки на прямую. Формула для нахождения расстояния может быть выведена аналогично расстоянию от точки до плоскости и имеет вид: 
Кривые второго порядка

|
Окружность
Окружностью называется геометрическое место точек, для каждой из которых, расстояние до фиксированной точки, называемой центром, постоянно.
Выведем уравнение окружности в декартовой системе координат. Пусть точка  - центр окружности,
- центр окружности,  - расстояние от центра до произвольной точки
- расстояние от центра до произвольной точки  , принадлежащей окружности (радиус окружности). По определению окружности
, принадлежащей окружности (радиус окружности). По определению окружности  , т.к.
, т.к.
 ,
,
откуда  . После возведения в квадрат обеих частей равенства, получим уравнение окружности радиуса
. После возведения в квадрат обеих частей равенства, получим уравнение окружности радиуса  с центром в точке
с центром в точке  :
:
 .
.
Если центр окружности находится в начале координат, то уравнение окружности примет вид:  .
.
Если в левой части уравнения  раскрыть скобки, привести подобные и ввести обозначения:
раскрыть скобки, привести подобные и ввести обозначения:  , то его можно записать в виде:
, то его можно записать в виде: 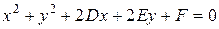 .
.
|
|
|
При умножении или делении обеих частей данного уравнения на произвольное число, отличное от 0, коэффициенты при  и
и  уже не будут равны 1, но должны быть равны друг другу.
уже не будут равны 1, но должны быть равны друг другу.
Пример. Найти координаты центра и радиус окружности, заданной уравнением  .
.
Сгруппируем слагаемые, содержащие переменные  и
и  , и вынесем за скобку имеющиеся общие множители:
, и вынесем за скобку имеющиеся общие множители:
 .
.
В скобках выделим полный квадрат:

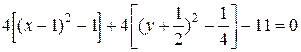 .
.
Раскрывая квадратные скобки и сокращая обе части уравнения на 4, получим
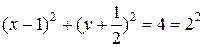 .
.
Сравнивая полученное уравнение с уравнением окружности в общем виде, найдем, что координаты центра  а радиус окружности
а радиус окружности  .
.
Эллипс
Эллипсом называется геометрическое место точек, для каждой из которых, сумма расстояний до двух фиксированных точек, называемых фокусами, постоянна и больше расстояния между фокусами.

|
Выведем уравнение эллипса в декартовой системе координат. Расположим фокусы эллипса на оси  симметрично началу координат в точках
симметрично началу координат в точках  и
и  .
. 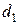 и
и  — расстояния от произвольной точки
— расстояния от произвольной точки  эллипса до фокусов. Тогда, по определению эллипса
эллипса до фокусов. Тогда, по определению эллипса  , где
, где  — сумма расстояний. Из определения также следует, что
— сумма расстояний. Из определения также следует, что  . Поскольку
. Поскольку
 ,
,
то  .
.
Преобразуем выписанное равенство, возведя вначале обе его части в квадрат:

Раскроем скобки, приведем подобные:

Введем обозначение  и разделим на 2 обе части уравнения:
и разделим на 2 обе части уравнения:
 или
или  .
.
Снова возведем в квадрат обе части равенства:
 .
.
После упрощения:
 или
или  .
.
Разделив обе части последнего равенства на 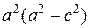 , получим каноническое уравнение эллипса:
, получим каноническое уравнение эллипса:
 .
.
В уравнении использовано обозначение  .
.

|
Из уравнения следует, что эллипс должен проходить через точки  , которые называются вершинами эллипса. Соединяя эти точки плавной линией, получим изображение эллипса, заданного каноническим уравнением.
, которые называются вершинами эллипса. Соединяя эти точки плавной линией, получим изображение эллипса, заданного каноническим уравнением.
Из рисунка видно, что эллипс имеет две оси симметрии и центр симметрии. Параметры  и
и  в уравнении эллипса называются его полуосями, т.к. равны половине длины соответствующих осей симметрии, отношение
в уравнении эллипса называются его полуосями, т.к. равны половине длины соответствующих осей симметрии, отношение  называется эксцентриситетом эллипса (
называется эксцентриситетом эллипса ( ).
).
|
|
|
Заметим, что если фокусы эллипса расположены на оси  , то
, то  , если же фокусы расположены на оси
, если же фокусы расположены на оси  , то наоборот,
, то наоборот, 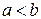 .
.
Пусть теперь центр эллипса расположен в произвольной точке  , а оси симметрии параллельны координатным осям. Проведем через центр эллипса вспомогательную систему координат
, а оси симметрии параллельны координатным осям. Проведем через центр эллипса вспомогательную систему координат  . В этой системе координат можно получить каноническое уравнение эллипса:
. В этой системе координат можно получить каноническое уравнение эллипса:

|
 .
.
Из рисунка видно, что координаты произвольной точки на эллипсе в исходной и вспомогательной системе координат связаны соотношениями:
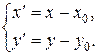
Используя эти равенства, получим уравнение эллипса со смещенным центром:
 .
.
Чтобы нарисовать эллипс по данному уравнению, нужно отметить центр эллипса  , провести через него вспомогательную систему координат
, провести через него вспомогательную систему координат  , отметить в ней вершины эллипса и соединить плавной линией.
, отметить в ней вершины эллипса и соединить плавной линией.

|
Пример. Изобразить эллипс по его уравнению:
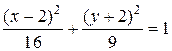
Координаты центра 
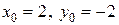 , отметим его на координатной плоскости. Проведем через
, отметим его на координатной плоскости. Проведем через  вспомогательные оси
вспомогательные оси  и
и  . Чтобы отметить вершины эллипса вправо и влево от
. Чтобы отметить вершины эллипса вправо и влево от  по оси
по оси  отложим по 4 единицы (т.к.
отложим по 4 единицы (т.к.  ), а вверх и вниз по оси
), а вверх и вниз по оси  отложим по 3 единицы (т.к.
отложим по 3 единицы (т.к. 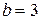 ). Соединим полученные точки плавной линией.
). Соединим полученные точки плавной линией.
Указанное в данном примере уравнение можно записать в другом виде:
 .
.
Обе части исходного уравнения умножили на 144.
Раскроем скобки и приведем подобные:
 .
.
В общем виде подобное уравнение можно записать так:
 . (*)
. (*)
Отметим, что в уравнении эллипса коэффициенты  и
и 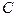 могут различаться по величине, но должны совпадать по знаку.
могут различаться по величине, но должны совпадать по знаку.
Обратный переход от уравнения вида (*) к уравнению со смещенным центром, можно выполнить аналогично примеру, рассмотренному в предыдущем пункте.
Гипербола
Гиперболой называется геометрическое место точек, для каждой из которых, модуль разности расстояний до двух фиксированных точек, называемых фокусами, имеет постоянное значение, меньшее расстояния между фокусами.
Если разместить фокусы гиперболы на  симметрично началу координат в точках
симметрично началу координат в точках  и
и  , обозначить расстояния от произвольной точки
, обозначить расстояния от произвольной точки  на гиперболе до фокусов
на гиперболе до фокусов 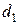 и
и  , а модуль их разности положить равным
, а модуль их разности положить равным  , то можно выписать условие для составления уравнения гиперболы в декартовой системе координат:
, то можно выписать условие для составления уравнения гиперболы в декартовой системе координат:
|
|
|

Преобразуя выписанное равенство подобно тому, как это было сделано при выводе уравнения эллипса, получим каноническое уравнение гиперболы:
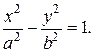
В уравнении использовано обозначение  (поскольку
(поскольку  ). Отношение
). Отношение  называется эксцентриситетом гиперболы.
называется эксцентриситетом гиперболы.
Если фокусы гиперболы расположить на  , уравнение гиперболы будет иметь вид:
, уравнение гиперболы будет иметь вид:
 или
или 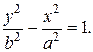
Такая гипербола называется сопряженной.
Для построения графика гиперболы, описываемой уравнением  , отметим, что он должен проходить через точки
, отметим, что он должен проходить через точки  и
и  - вершины гиперболы, кроме этого график не может пересекать
- вершины гиперболы, кроме этого график не может пересекать  .
.
Учитывая этот результат, график гиперболы строим следующим образом. Проводим прямые 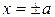 и
и  , эти линии ограничат основной прямоугольник гиперболы. Проведем прямые, совпадающие с диагоналями этого прямоугольника, это будут асимптоты гиперболы.
, эти линии ограничат основной прямоугольник гиперболы. Проведем прямые, совпадающие с диагоналями этого прямоугольника, это будут асимптоты гиперболы.

|
Отметим вершины  и
и  , затем проведем линии, плавно приближаясь от вершин к асимптотам.
, затем проведем линии, плавно приближаясь от вершин к асимптотам.
График гиперболы состоит из двух половин — ветвей, он имеет две оси симметрии и центр симметрии.
Пунктирной линией на рисунке нанесен график сопряженной гиперболы.
Уравнение гиперболы, центр симметрии которой находится в точке  , а оси симметрии параллельны координатным осям, получается аналогично подобному уравнению для эллипса:
, а оси симметрии параллельны координатным осям, получается аналогично подобному уравнению для эллипса:
 (**)
(**)
Отметим, что в уравнении гиперболы коэффициенты при  и
и  разных знаков.
разных знаков.
Пример. Установить, что уравнение 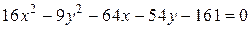
определяет гиперболу и построить ее.
Т.к. коэффициенты при  и
и  разных знаков, то можно предположить, что это уравнение гиперболы. Чтобы убедиться в этом, преобразуем заданное уравнение к виду (**).
разных знаков, то можно предположить, что это уравнение гиперболы. Чтобы убедиться в этом, преобразуем заданное уравнение к виду (**).
Сгруппируем слагаемые с  и
и  и вынесем имеющиеся при них общие множители за скобки:
и вынесем имеющиеся при них общие множители за скобки:
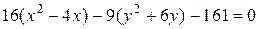 .
.
Выделим в скобках полный квадрат:
 ;
;
 ;
;
 ;
;
 .
.
Разделим обе части последнего равенства на 144:  .
.

|
Это уравнение гиперболы с центром в 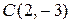 и полуосями
и полуосями  и
и 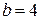 .
.
Отметим положение центра и проведем через него вспомогательные оси  и
и  . Отложим вправо и влево от
. Отложим вправо и влево от 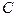 по 3 единицы и проведем прямые, параллельные оси
по 3 единицы и проведем прямые, параллельные оси  , отложив вверх и вниз по 4 единицы, проведем прямые, параллельные оси
, отложив вверх и вниз по 4 единицы, проведем прямые, параллельные оси  . Прямые, совпадающие с диагоналями получившегося прямоугольника являются асимптотами нашей гиперболы, отметим ее вершины на
. Прямые, совпадающие с диагоналями получившегося прямоугольника являются асимптотами нашей гиперболы, отметим ее вершины на  и построим график.
и построим график.
|
|
|
Парабола
Параболой называется геометрическое место точек, равноудаленных от заданной точки, называемой фокусом, и заданной прямой, называемой директрисой при условии, что директриса не проходит через фокус.
Чтобы составить уравнение параболы, разместим фокус в точке  , директрису проведем параллельно оси
, директрису проведем параллельно оси  через точку
через точку 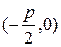 . Расстояние от произвольной точки
. Расстояние от произвольной точки  , принадлежащей параболе, до директрисы обозначим
, принадлежащей параболе, до директрисы обозначим  , а расстояние от
, а расстояние от  до фокуса —
до фокуса —  . По определению
. По определению  ;
;
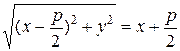 .
.
Возведем в квадрат обе части уравнения:  .
.

|
Раскрывая скобки и приводя подобные, получим каноническое уравнение параболы:
 .
.
Если 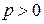 , то ветви параболы направлены в сторону положительного направления оси
, то ветви параболы направлены в сторону положительного направления оси  , если
, если  , то в обратную.
, то в обратную.
Если расположить директрису параллельно  , а фокус на оси
, а фокус на оси  , то получим уравнение параболы в виде:
, то получим уравнение параболы в виде: 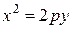
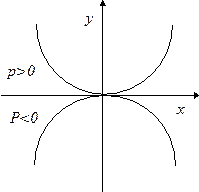
|
В соответствии со знаком параметра  ветви такой параболы будут смотреть вверх (
ветви такой параболы будут смотреть вверх (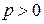 ) или вниз (
) или вниз ( ).
).
График параболы имеет только одну ось симметрии и не имеет центра симметрии. На графике имеется точка, называемая вершиной параболы.
Если вершина параболы находится не в начале координат, а в произвольной точке  , то уравнение параболы имеет вид:
, то уравнение параболы имеет вид:
 или
или  .
.
В уравнение параболы одна из координат входит в первой степени, а другая - во второй.
|
|
|


