 |
Пример решения контрольной работы №3
|
|
|
|
Задание 1
Прямая  проходит через точки
проходит через точки  и
и  , прямая
, прямая  проходит через точки
проходит через точки  и
и  . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Решение
Для составления уравнений прямых  и
и  используем уравнение прямой с угловым коэффициентом. Тогда уравнения прямых в общем виде можно записать так:
используем уравнение прямой с угловым коэффициентом. Тогда уравнения прямых в общем виде можно записать так:
 .
.
Учитывая, что координаты точки, принадлежащей прямой, должны удовлетворять её уравнению, для нахождения параметров уравнения первой прямой получим систему:

Решив систему, получим уравнение  :
:  .
.
Аналогично для нахождения параметров уравнения прямой  составим и решим систему:
составим и решим систему:

Тогда уравнение  :
: 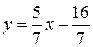 .
.
Точка пересечения прямых должна удовлетворять уравнениям обеих прямых, т.е. быть решением системы:
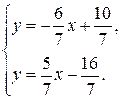
Решением этой системы являются  .
.

На рисунке отмечены заданные точки, проведены прямые, проходящие через них. Как видим, координаты точки их пересечения Е соответствуют их значениям, найденным аналитически.
Задание 2
Найти уравнение линии, для каждой точки которой отношение расстояния до точки  к расстоянию до прямой
к расстоянию до прямой  постоянно и равно
постоянно и равно  . Изобразить полученную линию на координатной плоскости.
. Изобразить полученную линию на координатной плоскости.
Решение
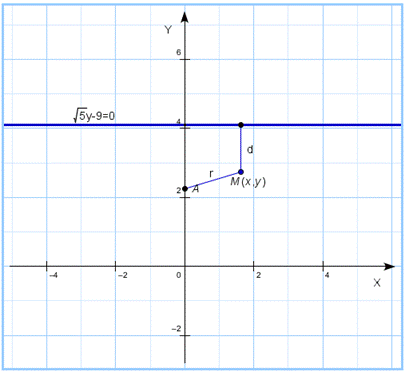
Для наглядности на чертеже изображена заданная прямая и заданная точка. Там же отмечена произвольная точка  , принадлежащая линии, уравнение которой нужно составить.
, принадлежащая линии, уравнение которой нужно составить.
Длина отрезка  равна модулю разности ординат точки на заданной прямой и точки М:
равна модулю разности ординат точки на заданной прямой и точки М:  . Расстояние
. Расстояние  между точками А и М находится по формуле:
между точками А и М находится по формуле:  .
.
По условию задачи:  .
.
 Подставляя в последнее равенство расстояния до точки и прямой, получим уравнение:
Подставляя в последнее равенство расстояния до точки и прямой, получим уравнение:
 .
.
Раскрываем скобки:
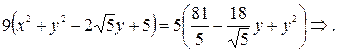
 Приведём подобные:
Приведём подобные: 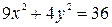 . Разделив обе части уравнения на 36, получим каноническое уравнение эллипса:
. Разделив обе части уравнения на 36, получим каноническое уравнение эллипса:  . Его изображение в соответствии с полученным уравнением приведено на рисунке.
. Его изображение в соответствии с полученным уравнением приведено на рисунке.
|
|
|
Задание 3
Найти точку пересечения прямой  и плоскости
и плоскости  . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Решение
Запишем уравнения прямой в параметрической форме:



Подставим полученные равенства в уравнение плоскости:

Тогда координаты точки пересечения:

Для того, чтобы отложить полученную точку в трёхмерной декартовой системе координат через значение абсциссы (10) проведём прямую, параллельную оси ординат. На ней от оси абсцисс отложим значение ординаты, равное 4. Из полученной точки вниз отложим значение аппликаты, равное -3.

Точка Е – это точка пересечения прямой и плоскости.
Задания контрольной работы №3
Вариант 1
Задание 1
Прямая  проходит через точки
проходит через точки 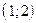 и
и  , прямая
, прямая  проходит через точки
проходит через точки  и
и  . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 2
Найти уравнение линии, для каждой точки которой отношение расстояния до точки  к расстоянию до прямой
к расстоянию до прямой  постоянно и равно
постоянно и равно  . Изобразить полученную линию на координатной плоскости.
. Изобразить полученную линию на координатной плоскости.
Задание 3
Найти точку пересечения прямой 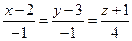 и плоскости
и плоскости  . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 2
Задание 1
Прямая  проходит через точки
проходит через точки  и
и 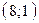 , прямая
, прямая  проходит через точки
проходит через точки  и
и  . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 2
Найти уравнение линии, для каждой точки которой отношение расстояния до точки  к расстоянию до прямой
к расстоянию до прямой 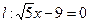 постоянно и равно
постоянно и равно  . Изобразить полученную линию на координатной плоскости
. Изобразить полученную линию на координатной плоскости
Задание 3
Найти точку пересечения прямой  и плоскости
и плоскости  . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 3
Задание 1
|
|
|
Прямая  проходит через точки
проходит через точки  и
и  , прямая
, прямая  проходит через точки
проходит через точки  и
и  . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 2
Найти уравнение линии, для каждой точки которой отношение расстояния до точки  к расстоянию до прямой
к расстоянию до прямой  постоянно и равно
постоянно и равно  . Изобразить полученную линию на координатной плоскости.
. Изобразить полученную линию на координатной плоскости.
Задание 3
Найти точку пересечения прямой  и плоскости
и плоскости  . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 4
Задание 1
Прямая  проходит через точки
проходит через точки  и
и  , прямая
, прямая  проходит через точки
проходит через точки  и
и  . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 2
Найти уравнение линии, для каждой точки которой отношение расстояния до точки 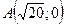 к расстоянию до прямой
к расстоянию до прямой  постоянно и равно
постоянно и равно  . Изобразить полученную линию на координатной плоскости.
. Изобразить полученную линию на координатной плоскости.
Задание 3
Найти точку пересечения прямой  и плоскости
и плоскости 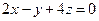 . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 5
Задание 1
Прямая  проходит через точки
проходит через точки  и
и  , прямая
, прямая  проходит через точки
проходит через точки  и
и  . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 2
Найти уравнение линии, для каждой точки которой отношение расстояния до точки  к расстоянию до прямой
к расстоянию до прямой  постоянно и равно
постоянно и равно  . Изобразить полученную линию на координатной плоскости.
. Изобразить полученную линию на координатной плоскости.
Задание 3
Найти точку пересечения прямой  и плоскости
и плоскости  . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 6
Задание 1
Прямая  проходит через точки
проходит через точки  и
и 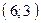 , прямая
, прямая  проходит через точки
проходит через точки 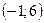 и
и  . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 2
Найти уравнение линии, для каждой точки которой отношение расстояния до точки  к расстоянию до прямой
к расстоянию до прямой  постоянно и равно
постоянно и равно  . Изобразить полученную линию на координатной плоскости.
. Изобразить полученную линию на координатной плоскости.
Задание 3
Найти точку пересечения прямой  и плоскости
и плоскости  . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 7
Задание 1
Прямая  проходит через точки
проходит через точки  и
и 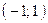 , прямая
, прямая  проходит через точки
проходит через точки  и
и  . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
|
|
|
Задание 2
Найти уравнение линии, для каждой точки которой отношение расстояния до точки  к расстоянию до прямой
к расстоянию до прямой  постоянно и равно
постоянно и равно  . Изобразить полученную линию на координатной плоскости.
. Изобразить полученную линию на координатной плоскости.
Задание 3
Найти точку пересечения прямой  и плоскости
и плоскости  . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 8
Задание 1
Прямая  проходит через точки
проходит через точки  и
и 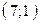 , прямая
, прямая  проходит через точки
проходит через точки  и
и  . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 2
Найти уравнение линии, для каждой точки которой отношение расстояния до точки  к расстоянию до прямой
к расстоянию до прямой  постоянно и равно
постоянно и равно  . Изобразить полученную линию на координатной плоскости.
. Изобразить полученную линию на координатной плоскости.
Задание 3
Найти точку пересечения прямой  и плоскости
и плоскости 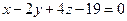 . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 9
Задание 1
Прямая  проходит через точки
проходит через точки  и
и  , прямая
, прямая  проходит через точки
проходит через точки 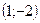 и
и  . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 2
Найти уравнение линии, для каждой точки которой отношение расстояния до точки  к расстоянию до прямой
к расстоянию до прямой  постоянно и равно
постоянно и равно  . Изобразить полученную линию на координатной плоскости.
. Изобразить полученную линию на координатной плоскости.
Задание 3
Найти точку пересечения прямой 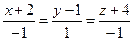 и плоскости
и плоскости  . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 10
Задание 1
Прямая  проходит через точки
проходит через точки  и
и  , прямая
, прямая  проходит через точки
проходит через точки  и
и 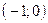 . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 2
Найти уравнение линии, для каждой точки которой отношение расстояния до точки  к расстоянию до прямой
к расстоянию до прямой  постоянно и равно
постоянно и равно  . Изобразить полученную линию на координатной плоскости.
. Изобразить полученную линию на координатной плоскости.
Задание 3
Найти точку пересечения прямой  и плоскости
и плоскости  . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Оглавление
Введение 3
Раздел 1. Контрольная работа по высшей математике №1 3
|
|
|
1.1. Теоретический материал по линейной алгебре 3
1.1.1. Комплексные числа и действия с ними 3
1.1.2. Матрицы и действия с ними 5
1.1.3. Решение квадратных неоднородных систем линейных алгебраических уравнений 13
1.2. Пример решения контрольной работы №1 18
1.3. Задания контрольной работы №1 19
Раздел 2. Контрольная работа по высшей математике №2 26
2.1. Теоретический материал по векторной алгебре 26
2.1.1. Векторы и действия с ними 26
2.1.2. Координатная форма представления векторов 29
2.2. Пример решения контрольной работы №2 31
2.3. Задания контрольной работы №2 33
Раздел 3. Контрольная работа по высшей математике №3 36
3.1. Теоретический материал по аналитической геометрии 36
3.1.1. Плоскость 36
3.1.2. Прямая в пространстве 39
3.1.3. Прямая на плоскости 41
3.1.4. Кривые второго порядка 43
3.2. Пример решения контрольной работы №3 49
3.3. Задания контрольной работы №3 53
|
|
|


