 |
Статистическая обработка результатов прямых равнорассеянных измерений
|
|
|
|
Под статистической обработкой результатов измерений здесь подразумевается обработка результатов многократных прямых измерений одной и той же физической величины. Их также называют «измерения с многократными наблюдениями» или «серия измерений».
Подготовка массива результатов наблюдений (многократных измерений) к статистической обработке заключается в «исправлении результатов измерений». Задача-минимум состоит в исключении из результатов измерений переменных систематических составляющих, задача-максимум – в исключении всех систематических составляющих. Методы выявления, оценки и исключения систематических погрешностей были рассмотрены ранее. Следует вспомнить, что любое исключение погрешностей не бывает абсолютным; в результатах могут содержаться невыявленные систематические составляющие, а также всегда остаются неисключенные остатки систематических погрешностей.
Невыявленные систематические погрешности – результат невнимательности или низкой квалификации метролога и обсуждению не подлежат. Неисключенные остатки систематических погрешностей следует оценить и сопоставить со случайной составляющей, чтобы признать пренебрежимо малыми или (при необходимости) учесть в представлении результатов измерений как это описано ниже.
Рассмотрим порядок статистической обработки исправленных результатов прямых равнорассеянных измерений одной и той же величины.
Обработку начинают с расчета среднего арифметического значения исправленных результатов наблюдений Ã (получение точечной оценки результата измерения)
n
à = (Σ xi.) /n
i =1
где хi – i -й результат наблюдения;
Затем возможно выполнение двух промежуточных операций для проверки правильности расчетов Ã:
|
|
|
Расчет отклонений Vi результатов наблюдений от среднего арифметического значения
Vi = Ã – xi.
Расчет суммы отклонений (отклонения суммируют с учетом знаков)
n
Σ Vi. ≈ 0
i =1
Если сумма отклонений практически равна нулю, расчеты значений Ã и Vi можно считать правильными, в противном случае необходимо перепроверить расчеты.
Расчет оценки с к о результатов наблюдений
где 
– точечная оценка результата измерения;
n – число результатов наблюдений;
– оценка среднего квадратического отклонения результатов наблюдений.
Далее при необходимости и возможности выполняют проверку гипотезы о сходимости эмпирического и теоретического распределений по критериям согласия.
При n > 50 для проверки принадлежности распределения к нормальному предпочтительно использование критериев Пирсона c2 или Мизеса-Смирнова w2. При 50 > n > 15 для проверки принадлежности распределения к нормальному предпочтительным является составной критерий (обозначим его W), механизм использования которого представлен в справочном приложении 1 ГОСТ 8.207.
Проверки по критериям согласия проводят с уровнем значимости q от 10 % до 2 %. Принятые значения уровней значимости приводят в описании методики выполнения измерений или обработки результатов измерений.
При n ≤ 15 проверку принадлежности распределения к нормальному не проводят, а качественную оценку формируют на основе априорной информации о виде (законе) распределения случайной величины, что позволяет затем перейти к соответствующей количественной оценке.
В случае обнаружения подозрительных результатов проводят статистическую проверку наличия/отсутствия результатов с грубыми погрешностями.
При нормальном распределении погрешностей можно применять упрощенную процедуру отбраковывания экстремальных отклонений, например, по критерию 3σ |Vextr| > 3σ.
|
|
|
Соблюдение неравенства позволяет утверждать, что проверяемый результат содержит грубую погрешность и должен исключаться из рассмотрения. Если отбракован хотя бы один результат с грубой погрешностью обработка повторяется с первого шага.
Оценку среднего квадратического отклонения результата измерения (оценку с к о среднего арифметического значения) определяют из зависимости
,
Где хi – i -й результат наблюдения; – результат измерения (среднее арифметическое исправленных результатов наблюдений); n – число результатов наблюдений;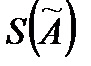 
– оценка среднего квадратического отклонения результата измерения.
При наличии ранее рассчитанного значения S можно воспользоваться той же зависимостью, представленной в виде
___
S(Ã) = S /√ n
Доверительные границы (без учета знака) случайной погрешности ε результата измерения рассчитывают из зависимости 
,
где t – коэффициент Стьюдента, зависящий от доверительной вероятности Р и числа результатов наблюдений n (находят из таблицы 8.1, взятой из справочного приложения 2 ГОСТ 8.207). В случае отсутствия значимых неисключенных систематических составляющих погрешности за значения границ погрешности результата измерения Δ принимают полученное значение ε.
Таблица 8.1 – Значение коэффициента t для случайной величины Y, имеющей распределение Стьюдента с n-1 степенями свободы
| n -1 | Р =0,95 | Р =0,99 | n -1 | Р =0,95 | Р =0,99 |
| 3,182 | 5,841 | 2,120 | 2,921 | ||
| 2,776 | 4,604 | 2,101 | 2,878 | ||
| 2,571 | 4,032 | 2,086 | 2,845 | ||
| 2,447 | 3,707 | 2,074 | 2,819 | ||
| 2,365 | 3,499 | 2,064 | 2,797 | ||
| 2,306 | 3,355 | 2,056 | 2,779 | ||
| 2,262 | 3,250 | 2,048 | 2,763 | ||
| 2,228 | 3,169 | 2,043 | 2,750 | ||
| 2,179 | 3,055 | ∞ | 1,960 | 2,576 | |
| 2,145 | 2,977 |
Обычно принимают Р = 0,95 или (в особых случаях) 0,99 и выше. Особые случаи – те, в которых результаты измерений связаны со здоровьем и безопасностью жизни людей, с возможными значительными экономическими потерями. Иногда принимают Р = 0,99 если существенно затруднены возможности повторения измерительного эксперимента или имеются иные причины.
При числе степеней свободы более 30, что приравнивается к бесконечности, чаще всего используют округленные значения коэффициента t, принимая t ≈ 2 при Р = 0,95 и t ≈ 2,6 при Р = 0,99, а при вероятности свыше 0,99 для простоты принимают t ≈ 3.
|
|
|
Далее при наличии известных оценок частных неисключенных систематических составляющих погрешностей Θ i рассчитывают границы неисключенной систематической составляющей погрешности
Неисключенная систематическая погрешность результата образуется из составляющих, в качестве которых могут быть неисключенные методические систематические погрешности, погрешности средств измерений и погрешности от других источников.
В качестве границ частных неисключенных систематических погрешностей принимают, например, пределы допускаемых погрешностей используемых мер (гирь, концевых мер длины) и/или других средств измерений, если эти погрешности представлены в их паспортах или иных документах. При использовании аттестованных средств измерений, если в результаты измерений вносится взятая из аттестата поправка, границей частной неисключенной систематической погрешности считают предельную погрешность аттестации.
Суммирование составляющих неисключенной систематической погрешности результата осуществляют на основе допущения о том, что все неисключенные систематические погрешности можно рассматривать как случайные величины. При отсутствии данных о виде распределений этих величин, их распределения принимают за равновероятные. Такое распределение приписывают погрешностям, поскольку его можно считать наихудшим из возможных вариантов.
Границы неисключенной систематической погрешности Θ результата измерения вычисляют путем построения композиции всех неисключенных систематических погрешностей. Эти границы (без учета знака) можно вычислить с использованием зависимости
,
где Θi – граница i -й неисключенной систематической погрешности; k – коэффициент, определяемый принятой доверительной вероятностью.
Значение коэффициента k при выбранной доверительной вероятности Р = 0,95 принимают равным 1,1.
Значение доверительной вероятности для вычисления границ неисключенной систематической погрешности принимают таким же, как и при вычислении доверительных границ случайной погрешности результата измерения.
|
|
|
При доверительной вероятности Р = 0,99 коэффициент k принимают равным 1,4, если число суммируемых неисключенных систематических погрешностей более четырех (m > 4). Если число суммируемых погрешностей равно четырем или менее четырех (m ≤ 4), то коэффициент k определяют по графику (рисунок 8.1) зависимостей k = f (m, l), представленному в стандарте ГОСТ 8.207.
Значение аргумента l рассчитывают по формуле
,
где Θ1 – составляющая, наиболее отличающаяся от других числовым значением, Θ2 – составляющая, ближайшая к Θ1.
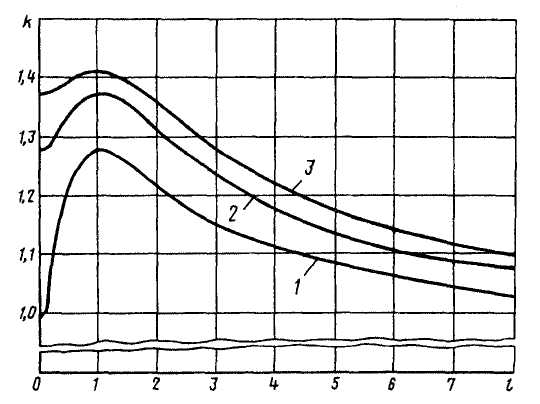
| Рисунок 8.1 – Графики зависимостей k =f (m, l): кривая 1 для m = 2; кривая 2 для m = 3 и кривая 3 для m = 4 |
Неисключенные систематические погрешности считают пренебрежимо малыми по сравнению со случайной составляющей если их значение менее 0,8 S(Ã). В таком случае принимают, что граница погрешности результата измерения Δ = ε.
Если значение неисключенной систематической погрешности превышает 8,0 S(Ã), то пренебрегают случайной погрешностью как пренебрежимо малой по сравнению с систематической и принимают, что граница погрешности результата Δ = Θ.
В стандарте говорится, что погрешность, возникающая из-за пренебрежения одной из составляющих погрешности результата измерения (случайной или неисключенной систематической), при выполнении указанных неравенств, не превышает 15 %.
Если отношение неисключенной систематической составляющей погрешности к случайной находится между двумя указанными пределами, т.е.
0,8 ≤ Θ / S(Ã) ≤ 8,0,
то границу погрешности результата измерения находят путем построения композиции распределений случайных и неисключенных систематических погрешностей. В таком случае допускается границы погрешности результата измерения Δ (без учета знака) вычислять с использованием зависимости
,
где K – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;
SΣ – оценка суммарного среднего квадратического отклонения результата измерения.
Коэффициент K вычисляют по эмпирической формуле
.
Оценку суммарного среднего квадратического отклонения результата измерения определяют из зависимости
,
__
где Θi / √ 3 – оценка среднего квадратического отклонения i -й неисключенной систематической погрешности, полученная на основе ранее представленного допущения о равновероятном распределении этих погрешностей в границах ±Θi, а соответственно Θi2/3 – дисперсия этого отклонения.
|
|
|
В стандарте сказано, что оформление результатов измерений должно соответствовать требованиям МИ 1317-86 «Методические указания. ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров».
Простейшая форма представления результатов измерений, предложенная ГОСТ 8.207 для случая симметричной доверительной погрешности
,
где 
– точечная оценка результата измерения,
Δ – доверительная граница результата измерений,
Р – доверительная вероятность.
Числовое значение точечной оценки результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности Δ.
При отсутствии данных о видах функций распределений случайных и неисключенных систематических составляющих погрешности, результаты измерений можно представить в форме
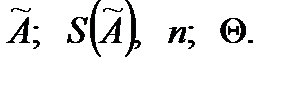
В случае если границы неисключенной систематической погрешности вычислены как композиция неисключенных частных систематических погрешностей, следует дополнительно указывать принятую в расчетах доверительную вероятность Р.
Эту форму нельзя считать окончательной, очевидна необходимость анализа погрешностей и дальнейшей обработки результатов для представления их в нормированном виде, соответствующем требованиям МИ 1317-86.
|
|
|
