 |
Система как четырехполюсник
|
|
|
|
Для описания изменения напряжений и токов во времени (процессов) в электрических цепях и устройствах используют дифференциальные уравнения и различные аналитические функции. В этом случае говорят о динамическом описании процессов и устройств. При этом, в некоторых случаях, описание удобнее вести в спектральном виде или в операторной форме.
Наиболее распространенным описанием электрических систем и устройств является представление этих устройств в виде четырехполюсника или «черного ящика» с некоторыми динамическими характеристиками. Схематическое представление системы, при таком подходе, показано на рис. 1.9. Связь между напряжением на входе системы Ux(t) и на её выходе Uy(t) однозначно определяется следующими функциями (см. рис. 1.9):
h(t) - переходная характеристика (реакция системы на единичное ступенчатое воздействие), характеризующая переход в новое состояние;
k(t) - импульсная характеристика (реакция системы на единичное импульсное воздействие в виде функции Дирака - δ(t));
К(w) - амплитудно-частотная характеристика;
W(p) – передаточная характеристика.
Переходная характеристика h(t) – это реакция системы на единичное ступенчатое воздействие в виде функции: Uх(t)=I(t)={u(t)=0 при t<to, u(t)=1 при t>to}.
Импульсная характеристика k (t) – это реакция на импульсное воздействие, т.е. на воздействие в виде единичного импульса Uх(t)=d(t)= { u(t)= 0при t<t o и при t> t o, u(t)= 1при t= t o}.
Рис. 1.9. Схематическое изображение динамической системы в виде четырехполюсника
Обычно достаточно одной из перечисленных функций, чтобы описать связь между выходной функцией и воздействием на входе с учетом предыстории системы, т.е. воздействий в предшествующие моменты времени. Однако при описании различных систем и процессов удобнее разные формы.
|
|
|
Рассмотрение ступенчатого и импульсного воздействий показывает, что импульсная функция d(t) является производной от ступенчатой функции I(t). Это позволяет заключить, что импульсная характеристика k(t) является производной от переходной функции h(t), т.е.
d (t)=dI(t)/d(t) и k(t)= dh(t)/d(t). (1.7)
Связь между процессами на входе и выходе четырехполюсника определяетсяинтегралом Дюамеля:
Uy(t) = Ux(0) h(t) + 
. (1.8)
Здесь t - текущее время интегрирования от 0 до t.
Формула (1.8) показывает связь изменений напряжения выходе четырехполюсника в зависимости от воздействия на входе и предыстории системы, выраженной с помощью переходной характеристики.
Аналогичную связь между процессами на входе и выходе можно выразить с помощью импульсной характеристики уравнением, которое называется уравнением Винера-Хопфа:
Uy(t) =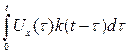 
. (1.9)
Формула (1.9) показывает связь изменений напряжения на выходе четырехполюсника в зависимости от воздействия на входе и предыстории системы, выраженной с помощью импульсной характеристики.
Амплитудно-частотная характеристика четырехполюсника – это последовательность отношений амплитуд гармонических напряжений на выходе устройства к напряжению на входе при разных частотах.
Из этого определения следует, что:
Uy¢¢(w)= K(w)×Uх¢(w), (1.10)
где Uх ¢(w)и Uy ¢(w)– амплитудно-частотные (спектральные) характеристики входной и выходной функции, а K (w) - амплитудно-частотная характеристика (АЧХ) системы.
Для более полного описания системы используют переход в частотную область с помощью преобразований Фурье в комплексном виде:
Uy (w) = W (w) ×Uх (w), (1.11)
где W (w) = K (w) ×e j j(w) = 
, (1.12)
Функция K (w) называется амплитудно-частотной характеристикой (АЧХ), а функция j(w) - фазо-частотной характеристикой (ФЧХ).
Соответственно, функции Uх (w) и Uy (w)в формуле (1.11) должны быть также представлены в комплексном виде, т.е. должны иметь амплитудно- и фазочастотные составляющие.
|
|
|
Передаточная характеристика – это амплитудно-частотная характеристика в операторном виде:
W(p) = 
, (1.13)
где p=s + jw - оператор Лапласа в комплексном виде, s -действительная (реальная) часть, jw - мнимая часть.
Наличие комплексной составляющей указывает на то, что оператор Лапласа позволяет описать колебательный характер переходных процессов.
Связь между входом и выходом системы определяется формулой аналогичной (1.11):
Uy(p) = V(p)×Uх(p), (1.14)
где Uх(p) и Uy(p) – преобразования Лапласа входной и выходной функции.
Функции изменения напряжения на входе Ux(t) (оригиналу) соответствует преобразование Лапласа Ux(p) (изображение).
Ux (p)= 
. (1.15)
Преобразование Лапласа Ux(p) от функции Ux(t) имеет действительную (реальную) и мнимую часть. Действительная часть описывает ступенчатые изменения напряжений и токов и затухание в переходных процессах, а мнимая представляет колебательные (частотные) составляющие процессов.
Если в операторе Лапласа убрать реальную часть, то можно заметить, что преобразование Лапласа в формуле (1.15) превращается в преобразование Фурье. Это означает, что преобразование Лапласа является обобщением преобразования Фурье.
Для ограниченного процесса (длительностью от 0 до T) имеем:
Ux(p)= 
. (1.16)
Зная изображение U(p) можно получить оригинал:
Ux(t) = 
, (1.17)
где с – постоянная.
Операторный метод удобен для описания электронных устройств и динамических процессов в электрических цепях.
Следует ещё раз отметить, что преобразование Фурье является частным случаем преобразования Лапласа. Аналогично, амплитудно-частотная характеристика является частным случаем передаточной характеристики или преобразованием Лапласа от импульсной характеристики. Таким образом, связь между процессами на входе и выходе четырехполюсника определяется формулами: (1.8), (1.9), (1.11) и (1.14).
Формулы (1.8) и (1.9) показывают связь между процессами на входе и выходе системы во временной области. Соответственно, формула (1.14) показывает связь между процессами на входе и выходе системы в операторной форме, а формула (1.11) – в частотной. Последняя формула применяется наиболее часто для исследования фильтров, усилителей, систем управления. Для её правильного применения необходимо помнить, что преобразование Фурье имеет две составляющие: амплитудно-частотную и фазо-частотную характеристики (АЧХ и ФЧХ).
|
|
|
Кибернетический подход
Кибернетика (теория управления) рассматривает динамические системы, выполняющие целевое назначение, под воздействием входных (управляющих) сигналов в условиях действия окружающей среды. При кибернетическом подходе оперируют такими понятиями как: объект управления, цель, целевая функция, орган управления, управляющее воздействие, обратная связь, алгоритм.
Управление - в широком, кибернетическом смысле - это действие, направленное на выполнение определенной цели. Наука об управлении - это обобщение приемов и методов управления техническими и живыми объектами.
Рис. 1.10. Схема взаимодействия участников управления при кибернетическом подходе
Под управлением понимают также процесс организации такого целенаправленного действия на объект управления, в результате которого выполняется целевое назначение системы с участием человека под влиянием окружающей среды (внешнего воздействия). При кибернетическом подходе выделяют тройку - субъект (оператор), объект управления, окружающая среда (внешние воздействия). Схема взаимодействия основных участников управления при таком подходе показана на рис. 1.11.
Рис. 1.11. Схема взаимодействия участников процесса управления
При более детальном кибернетическом подходе к описанию системы предполагается наличие следующих компонент:
- объект управления (динамическая система);
- цель, целевая функция;
- окружающая среда;
- датчики контроля состояния объекта и среды;
- орган управления, управляющее воздействие;
- обратная связь (осуществляется через датчики контроля состояния объекта).
Схема взаимодействия участников процесса управления приведена на рис. 6.8.
На основе приведенной схемы можно заключить, что процесс управления - это информационный процесс, включающий сбор, накопление, обработку и анализ информации, а также выработку решения в виде управляющего воздействия, направленного на достижение цели. Последняя схема показывает, что органом управления может быть оператор или управляющая машина (кибернетическое устройство).
|
|
|
|
|
|
