Временные системы в терминах «вход-выход»

Первая часть первого пред­положения о характере функционирования систем гласит: систе­ма функционирует во времени. Множество моментов времени t, в которые рассматривается функционирование системы, обозна­чим Т, t _ Т. Множество T будем считать подмножеством множе­ства действительных чисел. В частности, оно может быть конеч­ным или счетным. В зависимости от характера множества Т раз­личают: дискретное, непрерывное и дискретно-непрерывное вре­мя. На практике часто представляют интерес только такие мно­жества Т, элементы которых располагаются в изолированных точках числовой оси. В этом случае говорят, что система функци­онирует в дискретном времени, например контактные схемы, конечные автоматы, вычислительные устройства ЭВМ и т. д. Вместо моментов времени t ₀, t _l ,... часто пишут ряд натуральных чисел 0, 1,2,..., которые называются тактами.

Множество Т представляет собой множество некоторого (ко­нечного или бесконечного) интервала числовой оси. В этом слу­чае говорят, что система функционирует в непрерывном времени, например механические и электрические системы, системы, рас­сматриваемые в теории автоматического регулирования, и т. д.

Не исключены случаи, когда множество Т имеет дискретно-непрерывный характер: на одних интервалах числовой прямой моменты t _ Т заполняют их целиком, а на других — располага­ются в изолированных точках. Например: процесс производства автомобилей на конвейере; конвейер движется непрерывно, а го­товые автомобили сходят с него в дискретные моменты времени.

Входные сигналы системы. Второе и третье предположения о характере функционирования систем направлены на описание взаимодействия системы с внешней средой. На вход системы могут поступать входные сигналы х _ Х, где X — множество входных сигналов системы. Входной сигнал, поступивший в мо­мент времени t _ Т, обозначается x(t).

Входные сигналы могут описываться некоторым набором ха­рактеристик. Например, если входными сигналами АСУ аэро­дромом считать самолеты, поступившие в зону аэродрома, то каждый из них может быть описан набором параметров. Основными параметрами являются следующие: 1) координаты точки полета D, a, b (D -наклонная дальность, a - азимут и b- угол места); 2) вектор скорости V; 3) признаки, характеризующие тип самолета I. По этим параметрам оператор делает заключение о массе груза самолета G, требованиях к аэродромному обслуживанию и дает соответствующие команды экипажу самолета.

В общем случае будем предполагать, что входной сигнал X ₁_ X_i, где X_i — заданные множества (i = 1, n).

Прямое произведение X = X ₁´ X ₂´.... ´. Х_n называется прост­ранством входных сигналов. X_i - элементарные оси, входной сигнал х представляет собой точку пространства X, описываемую координатами x ₁, x ₂,..., х _n. В общем случае х _i _ Х.

При исследовании сложных систем приходится оперировать с группами входных сигналов, поступающих в моменты времени t _l< t ₂<...< t_k. Будем предполагать, что множеству X принадлежит и пустой сигнал х _{_}, означающий отсутствие сигнала в мо­мент t, x (t)= x _{_}.

Отображение x = L (t), ставящее в соответствие каждому t _ Т некоторый сигнал х _ X называется отображение ¦: Т ® Х. Обозначим через T^L множество моментов времени T^L _ Т, такое, что для любого t ^'_ T^L справедливо L (t ₁)_ x _{_}. Отображение x=L(t) бу­дем называть входным процессом систем, а совокупность упоря­доченных пар (t^', х) для всех t^' _ T^L ( где x = L(t')) — входным сообщением.

Чтобы задать конкретный входной процесс x=L(t), достаточ­но указать соответствующее ему входное сообщение (t, x_l)_t.

Интервал времени t₁<t<t₂ обозначим как (t₁,t₂), а полу­интервалы t_l<t и t<t₂ — через (t₁,t₂ ] и [ t₁,t₂), соответ­ственно интервал t_l_t_t₂ — через [ t₁,t₂ ].

Введем понятие «сужение отображения». Пусть множество X имеет область определения отображения y=f(x). Отображение y=g(x) c областью определения X * является сужением отображе­ния f(x) на множество X * в том и только в том случае, когда X*_X и g (x) =f(x) для каждого х_Х*.

В теории линейных систем фундаментальную роль играет следующая теорема.

Теорема. Пусть X и У — линейные алгебры над одним и тем же полем А. Система S Ì X´Y является линейной в том и только том случае, когда найдется такая глобальная реакция R, при которой X´ R=Z ®Y, причем

1. Z есть линейная алгебра над А;

2. существует пара таких линейных отображений

R1: Z®Y и R2: X ®Y,

что для всех (x,y) Î X´Y

R(x,z) = R1(x)+R2(z)

Отображение R называют линейной глобальной реакцией системы тогда, и только тогда, когда:

1. R согласуется с S, т.е. (x, y) Î S.

2. Z является линейной алгеброй над полем А скаляров линейных алгебр X и У.

Существуют два таких линейных отображений R1: Z®Y и R2: X ®Y, что для любых (x,y) Î X´Y

R(x, z) = R 1 (x)+R2(z)

В этом случае Z называют линейным объектом глобальных состояний системы, отображение R ₁: Z ® Y — глобальной реак­цией на состояние, a R ₂: X ® Y — глобальной реакцией на вход.

Модели систем в виде дифференциальных уравнений

Традиционными формами представления моделей являются системы уравнений в нормальной форме Коши, в виде линейных и нелинейных дифференциальных уравнений, графов, структурных схем. Они позволяют описывать и иерархические модели.

Нормальная форма Коши

Единообразное по форме и удобное для использования матричного аппарата математическое описание динамических (обычно «гладких») систем достигается в пространстве состояний с использованием переменных состояния, т. е. уравнений в форме Коши

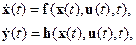(1.5)

где — векторы переменных состояния, входов, управления и выходов; 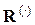— 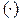-мерное эвклидово пространство; — гладкие отображения. Предполагается выполнение условия существования решений, а для большинства практических задач — их единственности. Условия существования и единственности решений выполняются, если принадлежит одному из следующих наиболее часто используемых классов функций: постоянные, кусочно-постоянные, кусочно-непрерывные, кусочно-гладкие, измеримые (локально-ограниченные), а функция — удовлетворяет условиям непрерывности Коши-Липшица.

Частным случаем представления динамических моделей в терминах «вход-состояние-выход» типа (1.5) являются L-системы.

L -системой называется система в которой выполняется соотношение

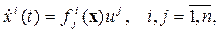
где , причем

Здесь [ F_i, F_j ] является коммутатором алгебры Ли векторного поля.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: