 |
Объединение агрегатов в структурные элементы
|
|
|
|
Отдельные агрегаты могут объединяться и создавать структурные элементы системы.
Типовые наборы структурных элементов Si приведены на рис. 1.13:
· последовательное соединение,
· параллельное соединение,
· каскадное соединение,
· соединение с обратной связью.
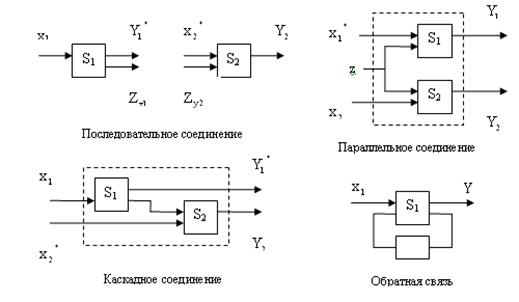
Рис. 1.13. Типовые соединения агрегатов в структурные элементы
Как правило, структурные элементы системы приобретают новые свойства по сравнению со свойствами отдельных агрегатов. Структурные элементы могут объединяться и создавать более сложные блоки и подсистемы, обладающие новыми свойствами и функциональными возможностями.
Абстрактная теория структурных схем и блоков
Абстрактная теория структурных схем и блоков предполагает наличие простого блока (агрегата), для которого определены функциональные связи между входными и выходными сигналами: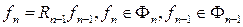 
, где f n-1 - входное множество сигналов, fn - выходное множество сигналов, R – оператор связи.
Таким образом, простой блок (агрегат) можно представить в виде, показанном на рис. 1.14.
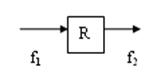
Рис. 1.14. Схема простого блока (агрегата)
Соединения блоков (агрегатов) приводят к появлению нового блока (агрегата) более высокого порядка, выполняющего более сложные функции.
Типовые наборы соединений блоков (агрегатов) следующие:
1) Последовательное соединение блоков
2) Параллельное соединение блоков
3) Замыкание обратной связью
Схема последовательного соединения блоков (агрегатов) представлена на рис. 1.15. Такая схема характерна для последовательного соединения триггеров. В результате формируется новый агрегат - двоичный счетчик импульсов.
Рис. 1.15. Схема последовательного соединения блоков (агрегатов)
|
|
|
Типовые параллельные соединения блоков (агрегатов) представлены на рис. 1.16.
Рис. 1.16. Схемы параллельного соединения блоков (агрегатов)
Схемы соединения блоков (агрегатов) с замыканием обратной связью приведена на рис. 1.17, где дано также формальное представление этого блока как нового агрегата.
Рис. 1.17. Схема соединения блоков (агрегатов) с замыканием обратной связью и её формальное представление
Множество R называется кольцом, если определены операции сложения и умножения с соблюдением правил коммутативности (перестановок) и ассоциативности (объединения).
Условие коммутативности: R1+R2= R2+R1; R1´R2= R2´R1.
Условие ассоциативности: (R1+R2)+R3=R1 +(R2+R3)+R2;
(R1´R2)´R2=R1´ (R2´R3).
Иерархические модели системы и структурная теория алгоритмов
Иерархический принцип построения модели является одним из признаков структурной сложности системы. Иерархический и составной характер построения системы обычно отражается и в её модели.
Вертикальная соподчиняемость - это управление подсистемами только вышестоящего уровня.
Право вмешательства - это обязательность действий вышестоящих подсистем.
Сложные системы имеют разные уровни (страты) по подчиненности.
Страты (слои) - уровни описания или абстрагирования.
Система представляется комплексом моделей - технологических, информационных и т.п. со своими наборами переменных.
Слои - уровни сложности принимаемого решения:
1-й уровень - срочное решение;
2-й уровень - неопределенность или неоднозначность выбора;
3-й уровень – необязательность выполнения вышестоящих решений.
Разбиение сложной системы или проблемы на простые происходит последовательно:
1 - слой выбор способа действия,
2 - слой адаптации (приспособления),
3 - слой самоорганизации.
Многоэшелонные системы
Система состоит из четко выраженных подсистем, некоторые из них являются принимающими решения. Соблюдается иерархия подсистем по подчиненности и принятию решений. Анализ и представление таких систем в виде агрегатов и других моделей осуществляют методом декомпозиции на подсистемы и элементы. При этом используют функционально-целевой принцип с выявлением сильных и слабых связей. Декомпозиция и агрегирование рассмотрены подробно в разделе 1.15.
|
|
|
|
|
|
