Средняя энергия теплового движения молекул.

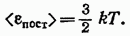
3. Распределение молекул по скоростям теплового движения (распределение Максвелла). Закон равномерного распределения энергии по степеням свободы. Внутренняя энергия идеального газа.

Распределение молекул по скоростям теплового движения(распределение Максвелла)

Не все молекулы движутся с одинаковыми скоростями. Среди них есть определенная доля молекул с малыми значениями скорости и, наоборот, некоторое число достаточно быстрых молекул. Однако, большая часть молекул обладает скоростями, значения которых группируются относительно наиболее вероятной при данной температуре величины. Такое распределение молекул по скоростям устанавливается в газе в результате обмена импульсом и энергией при многочисленных столкновениях молекул между собой и со стенками сосуда, Вид этого универсального (не меняющегося во времени) распределения молекул по скоростям, соответствующего состоянию теплового равновесия в газе, был впервые теоретически установлен Максвеллом. С помощью распределения Максвелла определяется относительная доля молекул, абсолютные скорости которых лежат в некотором узком интервале значений dv.

= ()^3\2

С помощью максвелловского распределения можно вычислить такие важные характеристики газа как средняя, среднеквадратичная и наиболее вероятная скорость теплового движения молекул, рассчитать среднее число столкновений молекул со стенкой сосуда и т.д. Средняя тепловая скорость молекул, например, которая представляет собой фактически средне-арифметическую скорость, определяется при этом формулой

= )^1\2

Наиболее вероятная скорость молекул, соответствующая максимуму кривых, определена как

V_в=()^1\2

Закон равномерного распределения энергии по степеням свободы.

В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул:для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия равная 1\2kT, а на каждую колебательную степень свободы – в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на неё приходится как кинетическая энергия, так и потенциальная, причем среднее значение потенциальной и кинетической энергии одинаковы. Значит средняя энергия молекулы:

<K>= kT - Закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы.

Внутренняя энергия идеального газа.

Внутренней энергией тела называют часть его полной энергии за вычетом кинетической энергии движения тела как целого и потенциальной энергии тела во внешнем поле. Таким образом, во внутреннюю энергию входят кинетическая энергия поступательного и вращательного движений молекул, потенциальная энергия их взаимодействия, энергия колебательного движения атомов в молекулах, а также энергия различных видов движения частиц в атомах.

В идеальном газе потенциальная энергия взаимодействия молекул пренебрежимо мала и внутренняя энергия равна сумме энергий отдельных молекул

Е_{вн= i}

где Ei — энергия отдельной молекулы. До сих пор мы пользовались представлением о молекулах как о материальных точках. Кинетическая энергия молекул считалась совпадающей с энергией их поступательного движения, а средняя кинетическая энергия молекулы полагалась равной <E_k>= . Эта энергия распределяется между тремя поступательными степенями свободы.

Ввиду полной беспорядочности движения молекул в газе все направления перемещения молекулы равновероятны. Поэтому на каждую степень свободы поступательного движения приходится в среднем энергия

<E_i> = <E_k>=

Представление о молекулах как о материальных точках оправдывается только для одноатомных газов. В случае многоатомных газов нужно рассматривать молекулы как сложные системы, способные вращаться как целое, причем атомы в них могут совершать колебания вблизи своих положений равновесия. Общее число степеней свободы молекулы при этом увеличивается.

Вспомним, что числом степеней свободы механической системы называется количество независимых параметров, с помощью которых может быть задано положение системы. Так, положение материальной точки в пространстве определяется заданием значений трех ее координат. В соответствии с этим материальная точка имеет три степени свободы.

Положение абсолютно твердого тела можно определить, задав три координаты его центра инерции и три угла, характеризующие возможные повороты тела в пространстве. Таким образом, абсолютно твердое тело имеет шесть степеней свободы — три поступательных и три вращательных.

N материальных точек, не связанных между собой, имеют 3N степеней свободы. Поскольку положение в пространстве системы как целого точно так же, как и положение абсолютно твердого тела определяется шестью параметрами, упомянутыми выше, то число степеней свободы такой системы равно 3·N-6. Это число соответствует возможным смещениям точек относительно друг друга около своих положений равновесия. Такой тип движения называется колебательным. Значит, количество колебательных степеней свободы и есть 3·N-6.

Энергия молекул, состоящих из некоторого числа атомов, не жестко связанных друг с другом, будет теперь складываться из энергии поступательного движения, вращательной энергии и энергии колебаний

Ei = Eпоступ + Eвращ +Eколеб

Нет причин полагать, что поступательное движение является в какой-то мере выделенным по сравнению с вращательным или колебательным. Поэтому следует считать, что по-прежнему на каждую степень свободы молекулы приходится энергия, равная kT/2. Однако следует учесть особенность, связанную с колебательным движением. Средняя энергия колебательного движения складывается из средней кинетической энергии и равной ей средней потенциальной энергии. Поэтому на каждую колебательную степень свободы приходится энергия, в два раза большая, чем на поступательные или вращательные степени свободы. Следовательно, средняя энергия молекулы должна равняться:

<Ei> = i·k·T

где i — сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:

i = iпоступ + iвращат + 2·iколеб.

Внутренняя энергия на один моль идеального газа

E_M= N_AkT =

4. Работа, совершаемая газом при расширении, ее зависимость от типа процесса.

Внутренняя энергия тела может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ подвергается сжатию в цилиндре под поршнем, то внешние силы совершают над газом некоторую положительную работу A'. В то же время силы давления, действующие со стороны газа на поршень, совершают работу A = –A'. Если объем газа изменился на малую величину ΔV, то газ совершает работу pSΔx = pΔV, где p – давление газа, S – площадь поршня, Δx – его перемещение.

При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна. В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой:

или в пределе при ΔVi → 0:

В изохорном процессе (V = const) газ работы не совершает, A = 0.

В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением: A = p (V2 – V1) = pΔV.

В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.

Первый закон термодинамики для изотермического процесса выражается соотношением Q = A.

Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.

Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими. Работа газа в адиабатическом процессе выражается через температуры T1 и T2 начального и конечного состояний:

A = CV (T2 – T1)

5. Количество теплоты. Первое начало термодинамики. Теплоемкость, ее зависимость от типа процесса. Адиабатный процесс.

Количество теплоты — энергия, которую получает или теряет тело при теплопередаче. Количество теплоты является одной из основных термодинамических величин. Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние.

Внутренняя энергия тела может изменяться за счет работы внешних сил. Для характеристики изменения внутренней энергии при теплообмене вводится величина, называемая количеством теплоты и обозначаемая Q.

Количество теплоты, передаваемое от одного тела к другому, может идти на нагревание тела, плавление, парообразование, либо выделяться при противоположных процессах – остывании тела, кристаллизации, конденсации. Теплота выделяется при сгорании топлива.

Между массой вещества и количеством теплоты, необходимым для его нагревания, существует прямая пропорциональная зависимость.

Количество теплоты, необходимое для нагревания тела или выделяющееся при его охлаждении, прямо пропорционально массе тела и изменению его температуры:

Q = cmΔT,

где с - удельная теплоемкость [Дж/кг·К], m - масса тела [кг], ΔT - изменение температуры [К]

Количество теплоты, необходимое для превращения жидкости в пар или выделяющееся при его конденсации, прямо пропорционально массе жидкости:

Q = Lm,

где L - удельная теплота парообразования [Дж/кг], m - масса тела [кг]

Количество теплоты, необходимое для плавления тела или выделяющееся при его кристаллизации, прямо пропорционально массе этого тела:

Q = λm,

где λ (лямбда) - удельная теплота плавления [Дж/кг], m - масса тела [кг]

Количество теплоты, выделяющееся при сгорании топлива, прямо пропорционально его массе:

Q = qm,

где q - удельная теплота сгорания [Дж/кг], m - масса тела [кг]

Удельная теплоемкость вещества показывает, чему равно количество теплоты, необходимое для нагревания или выделяющееся при охлаждении 1 кг вещества на 1 К.

Удельные теплоты парообразования, плавления, сгорания показывают, какое количество теплоты требуется для парообразования, плавления или выделяется при конденсации, кристаллизации, сгорании 1 кг вещества.

Адиабатный процесс — процесс, при котором отсутствует теплообмен между системой и окружающей средой.

Из первого начала термодинамики следует, что работа газа при адиабатном процессе совершается за счет его внутренней энергии:

(1).

С другой стороны, из уравнения Клапейрона-Менделеева следует:

(2).

Разделим уравнение (2) на уравнение (1):

, где

Проинтегрируем полученное уравнение: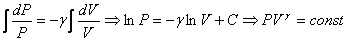

Таким образом, при адиабатном процессе

или — уравнение Пуассона.

С учетом уравнения Клапейрона-Менделеева

уравнение Пуассона может быть представлено в виде:

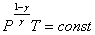или

или.

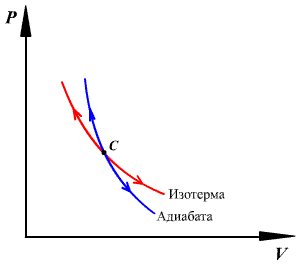
График адиабатного процесса — более крутая кривая, чем гипербола при изотермическом процессе. Это следует из выражения производной, полученной из уравнения Пуассона.

Работа газа при адиабатном процессе равна убыли внутренней энергии:

Теплоемкость.

ведем еще одну термодинамическую характеристику, а именно теплоемкость. Определим теплоемкость С как количество тепла, получаемое телом единичной массы для повышения его температуры на один градус: C = δQ/dT. Это количество тепла может быть различным (но всегда положительным!) при проведении нагрева в разных условиях. Из всех возможных вариантов предельными являются два. Пусть тело нагревается при постоянном объеме (скажем, оно имеет твердые недеформируемые стенки; см. рис. 4.1.1). В этом случае телом не может совершаться механической работы.

 

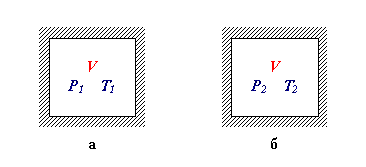
Рис. 4.1.1. Изохорный нагрев термодинамической системы (при условии сохранения объема постоянным): а) исходное состояние; б) конечное состояние

Все полученное за время dτ элементарное количество тепла δQ идет на изменение только внутренней энергии dU за счет изменения температуры на величину dT: δQ = dU. Тогда имеем как определение теплоемкости CV при постоянном объеме:

Рассмотрим теперь изобарный процесс получения системой тепловой энергии, т.е. процесс, происходящий при сохранении давления (см. рис. 4.1.2.).

 

Рис. 4.1.2. Изобарный нагрев термодинамической системы (при условии сохранения давления постоянным): а) исходное состояние; б) конечное состояние

В этом случае система изменяет объем, тем самым механически взаимодействуя с окружающей средой. Поэтому элементарное количество тепла δQ идет как на изменение внутренней энергии dU, так и на совершение механической работы P·dV:

δQ = dU + P·dV = dH

Отсюда, теплоемкость при постоянном давлении CP есть производная от энтальпии по температуре:

 

Установим взаимосвязь CP и CV. Для этого запишем:

 

Поскольку всегда Р > 0 и дV/дТ > 0, то CP всегда будет больше CV. Это очевидно, поскольку при постоянном давлении объем тела при нагреве увеличивается, и получаемое телом тепло расходуется не только на увеличение внутренней энергии (CV - составляющая), но и на совершение работы (P·V составляющая). Для идеальных газов, как известно из курса общей физики, уравнение состояния для одного моля газа записывается:

P·V = R·T

тогда имеем:

 

Взаимосвязь же CP и CV для конденсированного состояния имеет вид

где β - коэффициент объемного расширения, γ - сжимаемость, V - молярный (атомный)объем. Для связи CP с CV в твердых телах существует более простые полуэмпирические закономерности. Зависимость теплоемкости от температуры - уникальное физическое свойство каждого индивидуального вещества, его фундаментальная характеристика.

Теплоемкость твердых тел определяется главным образом колебаниями атомов в узлах кристаллической решетки. При низких температурах решеточная составляющая теплоемкости пропорциональна Т3 (теория Дебая, 1912 г.). Однако, начиная с некоторой температуры (которая для твердых тел называется характеристической температурой Дебая и обозначаемой θ), можно считать, что все уровни уже возбуждены. Дальнейшего увеличения значения решеточной составляющей теплоемкости уже не может происходить. Она выходит на некоторое предельное значение, равное СV = 3NA·ν, где ν - число атомов в молекуле вещества. Теоретический ход такой кривой показан на рис. 4.1.3.

 

Рис. 4.1.3. Зависимость относительной теплоемкости C/3ν твердых тел от приведенной температуры θ/T

При низких температурах (порядка 10 К) в твердых веществах с металлической связью основной вклад в теплоемкость вносят свободные электроны, теплоемкость которых пропорциональна температуре. Очевидно, что электронной составляющей теплоемкости для проведения расчетов металлургических процессов можно пренебречь.

При высоких температурах близких к температуре плавления вещества существенным (порядка 10 %) становится вакансионный вклад в теплоемкость. Этот вклад достаточно просто можно оценить, если известна температурная зависимость концентрации вакансий

n = A·exp(–U/RT), где U - энергия образования вакансии, А - константа.

Тогда вакансионный вклад в теплоемкость

Существенный вклад в теплоемкость твердых тел вносят и фазовые превращения 2-го рода, например магнитные превращения в ферромагнитных и антиферромагнитных материалах, а также упорядочение в ряде сплавов.

Теплоемкость газа, т.е. его свойство поглощать тепло, связано с возбуждением поступательных, вращательных и колебательных степеней свободы составляющих его атомов и молекул. Идеальный одноатомный газ имеет только 3 поступательные степени свободы и его теплоемкость равна CV = 3(R/2). Если молекулы газа многоатомны, то кроме поступательного движения при расчете теплоемкости необходимо учитывать вращательные и колебательные степени свободы внутри молекул (рис. 4.1.4.).

На каждую поступательную и вращательную степень свободы приходится теплоемкость, равная k/2, а на каждую колебательную – k (k – – постоянная Больцмана). Чем выше температура, тем большее количество поступательных, вращательных и колебательных уровней может быть возбуждено. Таким образом, теплоемкость газа при достаточно высокой температуре и низком давлении (условие идеальности реального газа)

CV = 3R/2 + nR/2 + mR

, где n – число вращательных степеней свободы, m – число колебательных степеней свободы. Для реальных газов при низких температурах, приближающихся к абсолютному нулю, поступательная и вращательная составляющие теплоемкости быстро уменьшаются, стремясь к нулю. Так, для молекул азота N2, эти составляющие резко отклоняются от предельных значений при температурах ниже 3 К. Колебательная же составляющая достигает своего предельного значения при высоких температурах порядка 3000 К. Расчет колебательной составляющей теплоемкости газа проводится по квантовой теории Эйнштейна. Очевидно, что при проведении расчетов высокотемпературных металлургических процессов с учетом присутствия газовой фазы необходимо учитывать именно колебательную составляющую теплоемкости газа. При расчете теплоемкости плазмы, которая часто используется в технологических процессах, необходимо учитывать и электронную составляющую плазмы. Пример реальной температурной зависимости теплоемкости газа показан на рис. 4.1.5.

Отметим, что для большинства жидкостей можно считать теплоемкость практически постоянной величиной, уже не зависящей от температуры.

Т.е., можно сделать следующий общий вывод: теплоемкость для всех тел есть монотонно возрастающая, строго положительная функция температуры, асимптотически стремящаяся к конечному пределу.

Величину значений теплоемкости можно оценить исходя из теоретических квантово-статистических соображений. Известны и эмпирические закономерности, позволяющие производить с достаточной точностью оценку теплоемкостей веществ, находящихся в различных агрегатных состояниях. Однако отметим, что сегодня, с достаточной для современных прикладных расчетов степенью точности, величина теплоемкости может быть определена только экспериментально. Результаты измерений при разных температурах аппроксимируют степенными полиномами, передающих температурную зависимость теплоемкости. Коэффициенты таких полиномов заносят в справочники термохимических величин.

6. Энтропия. Изменение энтропии при различных процессах. Закон возрастания энтропии. Второе начало термодинамики.

Функция состояния, полный дифференциал

которой равен , называется энтропией

Энтропия S – это отношение получен-ной или отданной теплоты к температу-ре, при которой происходил этот процесс

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: