Энергия электростатического поля.

Используем выражение, которое выражает энергию плоского конденсатора посредством зарядов и потенциалов, используя выражением для емкости плоского конденсатора (C=ε₀εS/d) и разности потенциалов между его обкладками (Δφ=Ed. Тогда
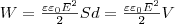(7)
где V= Sd — объем конденсатора. Формула (7) говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е.
Объемная плотность энергии электростатического поля (энергия единицы объема)
(8)

ЭЛЕКТРОМАГНЕТИЗМ

1. Электрический ток, его характеристики: сила и плотность тока.

Электри́ческий ток — направленное движение заряженных частиц.
Сила и плотность тока
Электрический ток имеет количественные характеристики: скалярную — силу тока, и векторную- плотность тока.
Сила тока — физическая величина, равная отношению количества заряда, прошедшего за некоторое время через поперечное сечение проводника, к величине этого промежутка времени (измеряется в амперах).
По закону Ома: l=U/R
Плотность тока — вектор, абсолютная величина которого равна отношению силы тока, протекающего через некоторое сечение проводника, перпендикулярное направлению тока, к площади этого сечения, а направление вектора совпадает с направлением движения положительных зарядов, образующих ток.
Согласно закону Ома в дифференциальной форме: J= E.

1. Однородный участок электрической цепи. Закон Ома в интегральной и дифференциальной (локальной) форме записи для однородного участка электрической цепи.

Однородный участок цепи-участок цепи, на котором не действуют сторонние силы(эдс).
Закон Ома в интегральной и дифференциальной форме записи для однородного участка электрической цепи:
лок: i=γE
Инт: I=U/R

1. Сопротивление проводников. Зависимость сопротивления проводника от его формы, материала и размеров. Зависимость сопротивления проводника от температуры. Сверхпроводимость.

Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему.
Зависимость сопротивления от размеров проводника
Для проводника длиной l и поперечным сечением S сопротивление определяется по формуле
R=pl/S
где ρ - удельное сопротивление - характеристика материала из которого изготовлен проводник.

Зависимость сопротивления от температуры
Причиной возникновения сопротивления является рассеяние (столкновение) носителей заряда на атомах решетки. При увеличении температуры, во-первых, увеличивается тепловая скорость электронов, во-вторых, увеличивается амплитуда колебания атомов относительно их равновесного положения. Указанные явления приводят к потерям энергии носителями заряда. Ток через проводник при этом уменьшится, т.е. сопротивление проводников при нагревании увеличивается.

Сверхпроводи́мость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения (критическая температура). Сверхпроводимость — квантовое явление. Оно характеризуется также эффектом Мейснера, заключающемся в полном вытеснении магнитного поля из объема сверхпроводника. Существование этого эффекта показывает, что сверхпроводимость не может быть описана просто как идеальная проводимость в классическом понимании.

1. Неоднородный участок электрической цепи. Закон Ома в интегральной и дифференциальной (локальной) форме записи для неоднородного участка электрической цепи.

неоднородный участок цепи- участок, где действует ЭДС

э.д.с. на участке 1 — 2 обозначим через а приложенную на концах участка разность

потенциалов — через .

Если ток проходит по неподвижным проводникам, образующим участок 1—2, то работа А ₁₂ всех сил (сторонних и электростатических), совершаемая над носителями тока, по закону сохранения и превращения энергии равна теплоте, выделяющейся на участке. Работа сил, совершаемая при перемещении заряда Q ₀ на участке 1 — 2

Э.д.с. как и сила тока I, — величина скалярная. Ее необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. Если э.д.с. способствует движению положительных зарядов в выбранном направлении (в направлении 1—2), то > 0. Если э.д.с. препятствует движению положительных зарядов в данном направлении, то < 0.

За время t в проводнике выделяется теплота

закон Ома для неоднородного участка цепи в интегральной форме

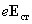На неоднородном участке цепи на носители тока действуют, кроме электростатических сил , еще и сторонние силы , следовательно, плотность тока в этих участках оказывается пропорциональной сумме напряженностей. Учет этого приводит к дифференциальной форме закон Ома для неоднородного участка цепи.

5. Закон Джоуля – Ленца для однородного участка электрической цепи в интегральной и дифференциальной (локальной) форме записи.

dQ = IU dt = I2R dt=~dt - выражение представляет собой закон Джоуля — Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э. X. Ленцем.

Выделим в проводнике элементарный цилиндрический объем dV = dS dl (ось цилиндра совпадает с направлением тока), сопротивление которого По за-

кону Джоуля — Ленца, за время dt в этом объеме выделится теплота

Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью

Используя дифференциальную форму закона Ома () и соотношение

получим

Формула является обобщенным выражением закона Джоуля —

Ленца в дифференциальной форме, пригодным для любого проводника.

В интегральной форме

1. Магнитное поле, его характеристики.

Опыт показывает, что, подобно тому, как в пространстве, окружающем электрические заряды, возникает электростатическое поле, так в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным.

Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные магниты. Название «магнитное поле» связывают с ориентацией магнитной стрелки под действием поля, создаваемого током (это явление впервые обнаружено датским физиком X. Эрстедом A777—1851)).

Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды. Важнейшая особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды. Опыт показывает, что характер воздействия магнитного поля на ток различен в зависимости от формы проводника, по которому течет ток, от расположения проводника и от направления тока. Следовательно, чтобы охарактеризовать магнитное поле, надо рассмотреть его действие на определенный ток.

Подобно тому, как при исследовании электростатического поля использовались точечные заряды, при исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле. Ориентация контура в пространстве характеризуется направлением нормали к контуру. В качестве положительного направления нормали принимается направление, связанное с током правилом правого винта, т. е. за положительное направление нормали принимается направление поступательного движения винта, головка которого вращается в направлении тока, идущего в рамке

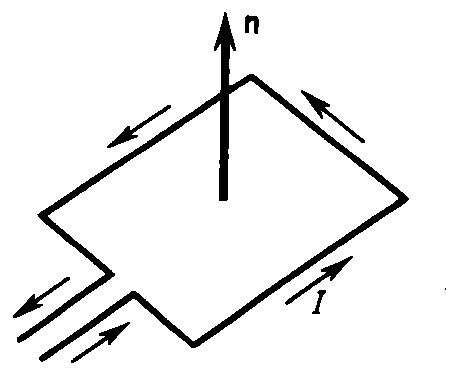Опыты показывают, что магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая ее определенным образом. Этот результат связывается с определенным направлением магнитного поля. За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положи- тельная нормаль к рамке.За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует на северный полюс магнитной стрелки, помещенной в данную точку.

 

Так как оба полюса магнитной стрелки лежат в близких точках поля, то силы, действующие на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направлением поля. Рамкой с током можно воспользоваться также и для количественного описания магнитного поля. Так как рамка с током испытывает ориентирующее действие поля, то на нее в магнитном поле действует пара сил. Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки:

где В — вектор магнитной индукции, являющейся количественной характеристикой магнитного поля, — вектор магнитного момента рамки с током. Для плоского контура с током где S — площадь поверхности контура (рамки), п—единичный вектор нормали к поверхности рамки. Направление совпадает, таким образом,с направлением положительной нормали. Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют различные вращающие моменты, однако отношение ( — максимальный

вращающий момент) для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля, называемой магнитной индукцией:

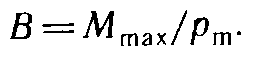
1. Закон Био - Савара – Лапласа, его применение для расчета индукции магнитного поля, созданного:

а) прямолинейным проводником с током конечной длины, бесконечно

длинным проводником с током;

б) в центре кругового проводника с током.

;

а) для расчета индукции магнитного поля, созданного прямолинейным проводником с током конечной длины, бесконечно длинным проводником с током

В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»).

б) магнитное полев центре кругового проводника с током

Все элементыкругового проводника с током создаютв центре магнитные поля одинаковогонаправления — вдоль нормали от витка. Поэтому сложение векторов dBможно заменить сложением их модулей. Все элементы проводника перпендикулярны радиусу-вектору(sin a = 1) и расстояние всех элементовпроводника до центра кругового токаодинаково и равно R.

 

1. Закон полного тока (теорема о циркуляции вектора индукции магнитного поля), его применение для расчета индукции поля длинного соленоида.

Циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной µ0 на алгебраическую сумму токов, охватываемых этим контуром, где n — числопроводников с токами,охватываемых контуром L произвольной формы.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: