Средняя длина свободного пробега молекул.

Эффективный диаметр

Молекулы газа находятся в состоянии хаотического движения непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы движутся равномерно прямолинейно, проходя при этом некоторый путь, который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна …, но так как мы имеем дело с огромным количеством молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега:

Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы.

Он зависит от скорости сталкивающихся молекул, то есть от температуры (эффективный диаметр уменьшается с увеличением За секунду (t = 1 с) молекула проходит в среднем путь равный по величине средней скорости. Если за 1 секунду она претерпевает в среднем z столкновений, то

Для определения ν считаем, что молекула имеет форму шара, и движется среди других неподвижных молекул. Эта молекула сталкивается только с теми молекулами, центры которых находятся на расстояниях d то есть лежат внутри “ломаного” цилиндра радиусом d

Среднее число столкновений за 1 секунду равно числу молекул в объёме “ломаного” цилиндра.

- среднее число столкновений

С учетом движения других молекул: 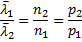Явления переноса объединяют группу процессов, связанных с неоднородностями плотности, температуры или скорости упорядоченного перемещения отдельных слоев вещества. Выравнивание неоднородностей приводит к возникновению явления переноса.Явления переноса в газах и жидкостях состоят в том, что в этих веществах возникает упорядоченный, направленный перенос массы (диффузия), импульса (внутренняя энергия) и внутренней энергии (теплопроводность). При этом в газах нарушается полная хаотичность движения молекул и распределение молекул по скоростям. Отклонениями от закона Максвелла объясняется направленный перенос физических характеристик вещества в явлениях переноса.

Будем рассматривать только одномерные явления, при которых физические величины, определяющие эти явления, зависят только от одной координаты

1. Теплопроводность.вление теплопроводности наблюдается, если в различных частях рассматриваемого газа температуры различны. Рассмотрение явления теплопроводности с микроскопической точки зрения показывает, что количество теплоты переносимое через площадку ΔS, перпендикулярную направлению переноса прямо пропорционально коэффициенту тепло проводимости χ, зависящему от рода вещества или газа, градиенту температуры еличины площадки ΔS и времени наблюдения Δt

Знак минус в законе Фурье показывает, что теплота переносится в направлении убывания температуры Т.

С молекулярно-кинетической точки зрения явления теплопроводности объясняется следующим образом. В той области объёма газа, где температура выше, кинетическая энергия хаотического теплового движения молекул больше, чем в той области, где температура ниже. В результате хаотического теплового движения молекулы переходят из области, где Т выше в область, где Т меньше. При этом они переносят с собой кинетическую энергию большую, той средней кинетической энергии, которой обладают молекулы в области с меньшей энергией. Вследствие постоянных столкновений молекул с течением времени происходит процесс выравнивания средних кинетических энергий, то есть выравнивание температур.

Коэффициент теплопроводности χ равен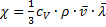

Физический смысл χ: коэффициент теплопроводности χ численно равен плотности теплового потока при градиенте температур равном 1

2. Диффузия Явление диффузии заключается в самопроизвольном перемешивании молекул различных газов или жидкостей. Явление диффузии наблюдается в твердых телах. В тех случаях, когда в химически чистом однородном газе концентрация молекул будет различной, наблюдается перенос молекул, приводящей к выравниванию плотностей (или концентраций) молекул. Это явление самодиффузии. Будем для простоты считать, что плотность неоднородна вдоль оси х. Рассмотрение явления самодиффузии с макроскопической точки зрения было сделано Фиком, который установил следующий закон: масса газа, переносимая через площадку ΔS, перпендикулярную к направлению переноса за время Δt прямо пропорциональна коэффициенту самодиффузии D, зависящему от рода газа, градиенту плотности величине площадки ΔS и времени наблюдения Δt.

знак минус показывает, что масса газа переносится в направлении убывания плотности. Коэффициент самодиффузии D численно равен массе газа переносимой за единицу времени через единичную площадку перпендикулярную направлению переноса, при градиенте плотности равном единице — плотность потока

Согласно кинетической теории газов

3. Внутреннее трение (вязкость) явление внутреннего трения наблюдается в том случае, когда различные слои газа движутся с разными скоростями. В этом случае более быстрее слои тормозятся движущимися медленнее. На макроскопическое движение слоев газа (то есть движение слоя как целого) оказывает воздействие микроскопическое тепловое движение молекул.

Рассмотрим слой газа 1, движущийся со скоростью v1 и слой газа 2, движущийся со скоростью v2 v1 > v2. В результате теплового хаотического движения молекула A из слоя 1 перейдет в слой 2 и изменит свой импульс от значения mv до какого-то значения mv’(v2 < v’< v1). Молекула В из слоя 2 в результате теплового хаотического движения перейдет в слой 1 и изменит свой импульс от значения mv2 до значения mv’’ (v2 < v’’ < v1), то есть молекулы ранее бывшие в слое 2, оказавшись в слое 1, при столкновении с его молекулами ускоряют свое упорядоченное движение, а упорядоченно движущиеся молекулы слоя 1 замедляются. Наоборот, при переходе молекул из более быстро движущегося слоя 1 в слой 2 они переносят большие импульсы имежмолекулярные соударения в слое 2 ускоряют движение молекул этого слоя. Явление внутреннего трения описывается законом Ньютона: Сила внутреннего трения F, действующая между двумя слоями газа прямо пропорциональная коэффициенту внутреннего трения η, градиенту скорости и величине площади ΔS.

- закон Ньютона.

Знак минус показывает, что сила внутреннего трения противоположна градиенту скорости, то есть импульс переноситься в направлении убывания скорости. Коэффициент внутреннего трения вычисляется по формуле

Связь между коэффициентами для явления переноса

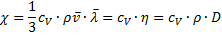
9. Уравнения неравновесных процессов (диффузии, теплопроводности, внутреннего трения).

В термодинамически неравновесных системах возникают особые необратимые процессы, называемые явлениями перевеса, в результате которых происходит пространственный перенос энергии, массы, импульса. К явлениям переноса относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса)

1. Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур. Перенос энергии в форме теплоты подчиняется закону Фурье:

λ

- плотность теплового потока — величина, определяемая энерги-ей, переносимой в форме теплоты в единицу времени через единичную площад-ку, перпендикулярную оси х/

λ-теплопроводность. - градиент температуры, равный скорости изменения температуры на единицу длины х в направле-нии нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры

2. Диффузия. Явление диффузии заключается в том, что происходит с а-мопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Явление диффузии для химически однородного газа подчиняется закону Функа:

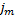=-D

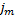- плотность потока массы — величина, определяемая массой ве-щества, диффундирующего в единицу времени через единичную площадку, пер-пендикулярную оси х, D — диффузия (коэффициент диффузии), dp/dx — градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности

3.Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различ-ными скоростями, заключается в том, что из-за хаотического теплового движе-ния происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличи-вается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

Взаимодействие двух слоев согласно второму закону Ньютона можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе.

= - n

- плотность потока импульса — величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х. - градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости.

ЭЛЕКТРОСТАТИКА

10. Закон Кулона. Электрический заряд, его свойства.

Закон Кулона: сила взаимодействия F между двумя неподвижными то-чечными зарядами, находящимися в вакууме, пропорциональна зарядам Q1и Q2

и обратно пропорциональна квадрату расстояния r между ними:
F= k

где k — коэффициент пропорциональности, зависящий от выбора системы единиц.

В векторной форме закон Кулона имеет вид

F =

Электрический заряд — величина релятивистски инвариантная, т. е. не

зависит от системы отсчета, а значит, не зависит от того, движется этот заряд

или покоится.

В зависимости от концентрации свободных зарядов тела делятся на проводники, диэлектрики и полупроводники. Проводники — тела, в которых

электрический заряд может перемещаться по всему его объему. Проводники

делятся на две группы: 1) проводники первого рода (металлы) — перенос в

них зарядов (свободных электронов) не сопровождается химическими превра-щениями; 2) проводники второго рода (например, расплавленные соли, рас-творы кислот) — перенос в них зарядов (положительных и отрицательных ио-нов) ведет к химическим изменениям. Диэлектрики (например, стекло, пласт-массы) — тела, в которых практически отсутствуют свободные заряды. Полу-проводники (например, германий, кремний) занимают промежуточное положе-ние между проводниками и диэлектриками. Указанное деление тел является

весьма условным, однако большое различие в них концентраций свободных за-рядов обусловливает огромные качественные различия в их поведении и оправ-дывает поэтому деление тел на проводники, диэлектрики и полупроводники.

Единица электрического заряда (производная единица, так как определя-ется через единицу силы тока) — кулон (Кл) — электрический заряд, проходя-щий через поперечное сечение проводника при силе тока 1 А за время 1 с.

11. Электростатическое поле, его характеристики (напряженность, потенциал), Принцип суперпозиции электростатических полей.

Электростатическое поле-вид материи,переносящей действие одной заряженной частицы на другое. Напряженность электростатического поля в данной точке есть физиче-ская величина, определяемая силой, действующей на пробный единичный по-ложительный заряд, помещенный в эту точку поля: E=

Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду:

 

Принцип суперпозиции электростатических полей - напряженность Е результирующего по-ля, создаваемого системой зарядов, равна геометрической сумме напряженно-стей полей, создаваемых в данной точке каждым из зарядов в отдельности. E=

12. Поток вектора напряженности электростатического поля. Теорема Гаусса для электростатического поля в вакууме.

Согласно принципу суперпозиции, напряженность Е поля диполя в произвольной точке

где Е+ и Е_ — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем напряженность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси.

Напряженность поля на продолжении оси диполя в точке А (рис. 123).

Как видно из рисунка, напряженность поля диполя в точке А направлена по оси

диполя и по модулю равна

 

 

 

Теорема Гаусса для электростатического поля в вакууме.

Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя выведенную немецким ученым К. Гауссом (1777—1855) теорему, определяющую поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность. В соответствии с формулой (79.3) поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре (рис. 124), равен

Этот результат справедлив для замкнутой поверхности любой формы. Действительно, если окружить сферу (рис. 124) произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность. Если замкнутая поверхность произвольной формы охватывает заряд то при пересечении любой выбранной линии напряженности с поверхностью она то входит в нее, то выходит из нее.

Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность. Бели замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее. Таким образом, для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен Q/0, т. е.

Знак потока совпадает со знаком заряда Q. Рассмотрим общий случай произвольной поверхности, окружающей n зарядов. В соответствии с принципом суперпозиции (80.2) напряженность Е поля, создаваемого всеми зарядами, равна сумме напряженностей Е, полей, создаваемых каждым зарядом в отдельности:

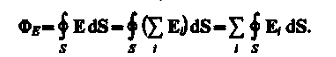
Формула (81.2) выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 0. Эта теорема выведена математически для векторного поля любой природы русским математиком М. В. Остроградским (1801—1862), а затем независимо от него применительно к электростатическому полю — К. Гауссом. В общем случае электрические заряды могут быть «размазаны» с некоторой объемной плотностью p = dQ/dV, различной в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, охватывающей некоторый объем V,

 

13. Расчет напряженности электростатического поля, созданного:

а) точечным зарядом, заряженной сферой;

в) равномерно заряженной бесконечной плоскостью;

г) равномерно заряженной длинной нитью (цилиндром).

А)- Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд — такой заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле). Если в поле, создаваемое зарядом Q, поместить пробный заряд Q0, то на него действует сила F, различная в разных точках поля, которая, согласно закону Кулона (78.2), пропорциональна пробному заряду Q0. Поэтому отношение F/Q0 не зависит от Q0 и характеризует электростатическое поле в той точке, где пробный заряд находится. Эта величина называется напряженностью и является силовой характеристикой электростатического поля. Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:

 

Направление вектора Е совпадает с направлением силы, действующей на положительный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положи тельного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду.

Б)Поле равномерно заряженной сферической поверхности.

Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверх-

ностной плотностью + . Благодаря равномерному распределению заряда по

поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому

линии напряженности направлены радиально (рис. 128).

 

Построим мысленно сферу радиуса r, имеющую общий центр с заряжен-

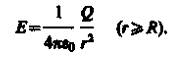
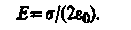ной сферой. Если г > R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса

 

откуда

 

При r>R поле убывает с расстоянием r по такому же закону, как у точеч-

ного заряда. График зависимости E от г приведен на рис. 129. Если , то

замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномер-

но заряженной сферической поверхности электростатическое поле отсутствует

(Е = 0).

 

 

В) Поле равномерно заряженной бесконечной плоскости.

Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотностью +

= dQ/dS — заряд, приходящийся на единицу поверхности.

Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно по-

строим цилиндр, основания которого параллельны заряженной плоскости, а ось

перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cos = 0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме

потоков сквозь его основания (площади оснований равны и для основания En

совпадает с E), т. е. равен 2ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен S. Согласно теореме Гаусса (81.2), 2ES = S/ 0,

откуда

 

Из формулы вытекает, что Е не зависит от длины цилиндра, т. е.

напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно..

 

 

Г)

 

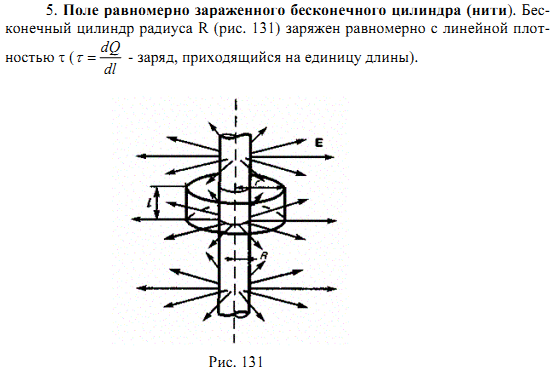
Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен

 

 

Если г < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области E = 0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (82.5), внутри же его поле отсутствует.

14. Работа кулоновских сил по перемещению заряда. Напряженность как градиент потенциала. Эквипотенциальные поверхности.

Работа кулоновских сил по перемещению заряда

Работа, совершаемая силами электростатического поля при перемещении заряда Q0 из точки 1 в точку 2 может быть представлена так:

где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения.

Если перемещать заряд Q0 из произвольной точки за пределы поля, т. е. в бесконечность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, согласно (84.6), А =О0, откуда

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: