Электроемкость уединенного проводника

Рассмотрим уединенный проводник,т. е. проводник, который удален от других проводников, тел и зарядов. Его потенци­ал, согласно, прямо пропорциона­лен заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряженными, принимают различные по­тенциалы. Поэтому для уединенного про­водника можно записать

Величину

называют электроемкостью (или просто емкостью) уединенного проводника. Ем­кость уединенного проводника определяет­ся зарядом, сообщение которого провод­нику изменяет его потенциал на единицу.

Емкость проводника зависит от его размеров и формы, но не зависит от мате­риала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциа­ла. Сказанное не противоречит формуле, так как она лишь показывает, что емкость уединенного проводника прямо пропорциональна его заряду и обратно пропорциональна потенциалу.

Единица электроемкости — фарад (Ф): 1Ф—емкость такого уединенного проводника, потенциал которого изменяет­ся на IB при сообщении ему наряда в 1 Кл.

Согласно, потенциал уединенно­го шара радиуса R, находящегося в одно­родной среде с диэлектрической проницае­мостью ε, равен

Используя формулы, получим что емкость шара

Отсюда следует, что емкостью в 1 Ф обла­дал бы уединенный шар, находящийся в вакууме и имеющий радиус R=C/(4π 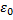) 9- 10⁶ км, что примерно в 1400 раз больше радиуса Земли (элек­троемкость Земли С 0,7мФ). Следова­тельно, фарад — очень большая величина, поэтому на практике используются доль­ные единицы — миллифарад (мФ), микро­фарад (мкФ), нанофарад (нФ), пикофа-рад (пФ). Из формулы вытекает также, что единица электрической посто­янной 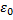фарад на метр (Ф/м)

Конденсаторы

Для того чтобы про­водник обладал большой емкостью, он дол­жен иметь очень большие размеры. На практике, однако, необходимы устройства, обладающие способностью при малых раз­мерах и небольших относительно окружа­ющих тел потенциалах накапливать зна­чительные по величине заряды, иными сло­вами, обладать большой емкостью. Эти устройства получили название конденса­торов.

Конденсатор состоит из двух провод­ников (обкладок), разделенных диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэ­тому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1)две плоские пластины; 2) два коакси­альных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.

Под емкостью конденсатора по­нимается физическая величина, равная отношению заряда Q, накопленного в кон­денсаторе, к разности потенциалов ( - ) между его обкладками:

24. Соединение конденсаторов.

При параллельном соединении конденсаторов заряд батареи равен q=q1+q2, aUодинаково и равно разности потенциалов. Электроемкость батареи (С) равна С=С1+С2, при nконденсаторах С=сумме всех электроемкостей.

При последовательном соединении конденсаторов с электроемкостями С1 и С2 общий заряд батареи равен заряду каждого конденсатора (q=q1=q2). Общее Uравно сумме напряжений на отдельных конденсаторах: U=U1+U2. Электроемкость батареи двух последовательныхконденсаторов: 1\С=1\С1+1\С2 или С=С1С2/(С1+С2). При соединении nконденсаторов С=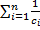

25. Энергия системы зарядов. Энергия уединенного заряженного проводника.

электростатические силы взаимодействия консервативны; значит, система зарядов обладает потенциальной энергией.

W1=Q1*ϕ12; W2=Q2*ϕ21

где φ₁₂ и φ₂₁ — соответственно потенциалы, которые создаются зарядом Q₂ в точке нахождения заряда Q₁ и зарядом Q₁ в точке нахождения заряда Q₂. Согласно,
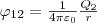и
поэтому W₁ = W₂ = W и

Добавляя к нашей системе из двух зарядов последовательно заряды Q₃, Q₄,..., можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна

(1)
где φ_i — потенциал, который создается в точке, где находится заряд Q_i, всеми зарядами, кроме i-го.

Энергия уединенного заряженного проводника:

Рассмотрим уединенный проводник, заряд, потенциал и емкость которого соответственно равны Q, φ и С. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, при этом затратив на это работу, которая равна
-элементарная работа сил электрического поля заряженного проводника">
Чтобы зарядить тело от нулевого потенциала до φ, нужно совершить работу

(2)
Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:
(3)
Формулу (3) можно также получить и условия, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Если φ - потенциал проводника, найдем

где Q=∑Q_i - заряд проводника.

26. Энергия заряженного конденсатора. Энергия электростатического поля.

Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы равна

где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора.