 |
Основные формулы. Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси х. Скорость мгновенная
|
|
|
|
Основные формулы
Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси х
x = f(t),
где f(t) – некоторая функция времени.
Скорость мгновенная
.
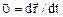Проекция мгновенной скорости на ось х
.
Проекция средней скорости на ось х
.
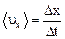Средняя путевая скорость
,
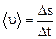где Δ s – путь, пройденный точкой за интервал времени Δ t. Путь Δ s в отличие от разности координат Δ х = х2 – х1 не может убывать и принимать отрицательные значения, т. е. Δ s ≥ 0.
Ускорение мгновенное
.
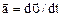Тангенциальное ускорение
.
Нормальное ускорение
.
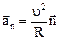Полное ускорение
, 
.
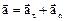Кинематическое уравнение движения материальной точки по окружности
φ = f(t).
Модуль угловой скорости
.
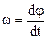Модуль углового ускорения
.
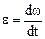Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:
.
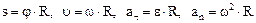где υ – модуль линейной скорости; аτ и аn – модули тангенциального и нормального ускорений; ω – модуль угловой скорости; ε – модуль углового ускорения; R – радиус окружности.
Модуль полного ускорения
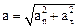, или 
.
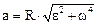Кинематическое уравнение гармонических колебаний материальной точки
х = А∙ cos(ω t + φ ),
где х – смещение; А – амплитуда колебаний; ω – угловая или циклическая частота; φ – начальная фаза.
Период малых колебания маятников:
а) пружинного и математического
;
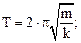
б) физического
.
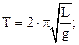
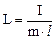где m – масса маятника; k – жесткость пружины; I – момент инерции маятника; g – ускорение свободного падения; l – расстояние от точки подвеса до центра масс, L – приведенная длина.
Скорость и ускорение материальной точки, совершающей гармонические колебания
|
|
|
υ = –А∙ ω ∙ sin(ω t + φ ), a = –А∙ ω 2∙ cos(ω t + φ ).
Сложение гармонических колебаний одного направления и одинаковой частоты:
а) амплитуда результирующего колебания
;
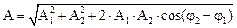б) начальная фаза результирующего колебания
.
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях
х = А1∙ cos(ω t); y = А2∙ cos(ω t + φ ):
а) y =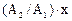 
, если разность фаз φ = 0;
б) y = – 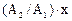, если разность фаз φ = ±π;
в)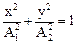 
, если разность фаз φ = ±π /2.
Уравнение плоской бегущей волны
,
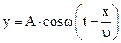где y – смещение любой из точек среды с координатой х в момент t; υ – скорость распространения колебаний в среде.
Связь разности фаз Δ φ колебаний с расстоянием Δ х между точками среды, отсчитанным в направлении распространения колебаний:
,
где λ – длина волны.
Импульс материальной точки массой m, движущейся со скоростью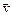 
,
.
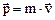Второй закон Ньютона (основное уравнение динамики поступательного движения)
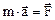или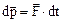 
,
где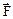 
– результирующая сила, действующая на материальную точку.
Силы, рассматриваемые в механике:
а) сила упругости
,
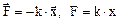где k – коэффициент упругости (в случае пружины – жесткость); х – абсолютная деформация;
б) сила тяжести
,
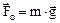где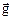 
– напряженность гравитационного поля (ускорение свободного падения);
в) сила гравитационного взаимодействия
,
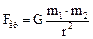где G – гравитационная постоянная; m1 и m2 – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки);
г) сила трения (скольжения)
Fтр = μ ∙ N,
где μ – коэффициент трения; N – сила нормального давления.
Закон сохранения импульса для изолированной системы
,
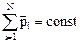или для двух тел (i = 2)
,
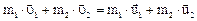где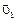 
и 
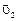– скорости тел в момент времени, принятый за начальный; 
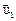и 
– скорости тех же тел в момент времени, принятый за конечный.
|
|
|
Кинетическая энергия тела, движущегося поступательно,
Ек = m∙ υ 2/2, или Ек = р2/(2m).
Потенциальная энергия:
а) упругодеформированной пружины
Еп = (k∙ x2)/2,
где k – жесткость пружины; х – абсолютная деформация;
б) гравитационного взаимодействия
Еп = –G∙ m1∙ m2/r,
где G – гравитационная постоянная; m1 и m2 – массы взаимодействующих тел; r – расстояние между ними (тела рассматриваются как материальные точки);
в) тела, находящегося в однородном поле силы тяжести,
Еп = m∙ g∙ h,
где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h< < R, где R – радиус Земли).
|
|
|
