 |
Закон сохранения механической энергии
|
|
|
|
Закон сохранения механической энергии
Е = Ек + Еп = const.
Работа силы F
.
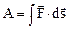Мгновенная мощность
.
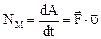Средняя мощность
.
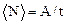Работа А, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:
А = Δ Ек = Ек2 – Ек1.
Момент инерции материальной точки
I = m∙ r2,
где r – расстояние до оси вращения.
Момент инерции твердого тела
.
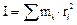Моменты инерции некоторых тел массой m относительно оси, проходящей через центр масс:
а) стержня длинойlотносительно оси, перпендикулярной стержню,
I = (m∙ l2)/12;
б) обруча (тонкостенного цилиндра) радиусом Rотносительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра),
I = m∙ R2;
в) диска радиусом R относительно оси, перпендикулярной плоскости диска,
I = (m∙ R2)/2;
г) шара радиусом R
I = (2∙ m∙ R2)/5.
Момент инерции тела массой m относительно произвольной оси (теорема Штейнера)
I = I0 + m∙ d2,
где I0 – момент инерции относительно параллельной оси, проходящей через центр масс; d – расстояние между осями.
Момент силы
.
Величина момента силы
M = F∙ r∙ sinα,
где α – угол между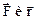 
.
Момент импульса твердого тела
.
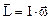Основное уравнение динамики вращательного движения
.
Закон сохранения момента импульса для изолированной системы
.
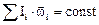Работа при вращательном движении
.
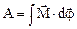Кинетическая энергия тела, вращающегося вокруг неподвижной оси,
.
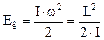Количество вещества
ν = N/NA = m/M,
где N – число молекул; NA – постоянная Авогадро; m – масса вещества; М – молярная масса.
Количество вещества смеси газов
ν = ν 1 + ν 2 + …+ ν n = N1/NA + N2/NA +…+ Nn/NA
|
|
|
или
ν = m1/M1 + m2/M2 +…+ mn/Mn,
где ν i, Ni, mi, Mi – соответственно количество вещества, число молекул, масса, молярная масса i-го компонента смеси.
Уравнение Менделеева – Клапейрона
p∙ V = ν ∙ R∙ T,
где р – давление газа; V – его объем; R – молярная газовая постоянная; Т – термодинамическая температура.
Опытные газовые законы, являющиеся частными случаями уравнения Менделеева – Клапейрона для изопроцессов:
а) закон Бойля – Мариотта (изотермический процесс: Т = const, m = const)
p∙ V = const,
или для двух состояний газа
p1∙ V1 = p2∙ V2;
б) закон Гей – Люссака (изобарный процесс: р = const,
m = const)
V/T = const,
или для двух состояний
V1/T1 = V2/T2;
в) закон Шарля (изохорный процесс: V = const, m = const)
р/Т = const,
или для двух состояний
р1/Т1 = р2/Т2;
г) объединенный газовый закон (m = const)
,
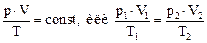где р1, V1, T1 – давление, объем и температура газа в начальном состоянии; р2, V2, T2 – те же величины в конечном состоянии.
Закон Дальтона, определяющий давление смеси газов,
р = р1 + р2 +…+рn,
где рi – парциальные давления компонентов смеси; n – число компонентов смеси.
Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.
Молярная масса смеси газов
,
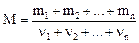где mi – масса i-го компонента смеси; ν i = mi/Mi – количество вещества i-го компонента смеси; n – число компонентов смеси.
Массовая доля i-го компонента смеси газа (в долях единицы или процентах)
ω i = mi/m,
где m – масса смеси.
Концентрация молекул
n = N/V = NA∙ ρ /M,
где N – число молекул, содержащихся в данной системе; ρ – плотность вещества; V – объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.
Уравнение молекулярно-кинетической теории газов
,
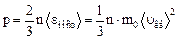где n –концентрация молекул;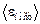 
– средняя кинетическая энергия поступательного движения молекулы, m0 – масса молекулы; 
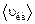– средняя квадратичная скорость.
|
|
|
Средняя энергия молекулы
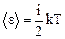
где i – число степеней свободы; k – постоянная Больцмана.
|
|
|
