Задачи. ПРИЛОЖЕНИЯ

Задачи

1. Под действием какой силы при прямолинейном движении тела изменение его координаты со временем происходит по закону
х = 10 + 5∙ t - 10∙ t²? Масса тела m = 2 кг.

2. Найти закон движения тела массой 1 кг под действием постоянной силы 10 Н, если в момент t = 0 тело покоилось в начале координат (х = 0).

3. Найти закон движения тела массой 1 кг под действием постоянной силы 1 Н, если в момент t = 0 начальная координата х = 0 и υ ₀ = 5 м/с.

4. Тело брошено под углом α = 30⁰ к горизонту со скоростью
υ ₀ = 30 м/с. Каковы будут нормальное а_n и тангенциальное а_τ ускорения тела через время t = 1 c после начала движения.

5. Тело массой 2 кг движется с ускорением, изменяющимся по закону а = 5∙ t – 10. Определить силу, действующую на тело через 5 с после начала действия, и скорость в конце пятой секунды.

6. Сплошной шар массой 1 кг и радиусом 5 см вращается вокруг оси, проходящей через его центр. Закон вращения шара выражается уравнением φ = 10 + 5∙ t – 2∙ t². В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. Определить эту силу и тормозящий момент.

7. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 100 м. Закон движения автомобиля выражается уравнением s = 100 + 10∙ t – 0. 5∙ t². найти скорость автомобиля, его тангенциальное, нормальное и полное ускорение в конце пятой секунды.

8. Материальная точка движется по окружности, радиус которой 20 м. Зависимость пути, пройденного точкой, от времени выражается уравнением s = t³ + 4∙ t² – t + 8. Определить пройденный путь, угловую скорость и угловое ускорение точки через 3с от начала ее движения.

9. Материальная точка движется по окружности радиусом 1 м согласно уравнению s = 8∙ t – 0. 2∙ t³. Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.

10. Тело вращается равноускоренно с начальной угловой скоростью 5 с^-1 и угловым ускорением 1 с^-2. Сколько оборотов сделает тело за 10 с?

11. При горизонтальном полете со скоростью υ = 250 м/с снаряд массой m = 8 кг разорвался на две части. Большая часть массой m₁ = 6 кг получила скорость u₁ = 400 м/с в направлении полета снаряда. Определить модуль и направление скорости u₂ меньшей части снаряда.

12. С тележки, свободно движущейся по горизонтальному пути со скоростью υ ₁ = 3 м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной u₁ = 4 м/с. Определить горизонтальную составляющую скорости u_2x человека при прыжке относительно тележки. Масса тележки m₁ = 210 кг, масса человека m₂ = 70 кг.

13. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом α = 30⁰ к линии горизонта. Определить скорость u₂ отката платформы, если снаряд вылетает со скоростью u₁ = 480 м/с. Масса платформы с орудием и снарядами m₂ = 18 т, масса снаряда m₁ = 60 кг.

14. Человек массой m₁ = 70 кг, бегущий со скоростью υ ₁ = 9 км/ч, догоняет тележку массой m₂ = 190 кг, движущуюся со скоростью υ ₂ = 3. 6 км/ч, и вскакивает на нее. С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?

15. Конькобежец, стоя на коньках на льду, бросает камень массой m₁ = 2. 5 кг под углом α = 30⁰ к линии горизонта со скоростью υ = 10 м/с. Какова будет начальная скорость υ ₀ движения конькобежца, если масса его m₂ = 60 кг? Перемещением конькобежца во время броска пренебречь.

16. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m₁ = 60 кг, масса доски m₂ = 20 кг. С какой скоростью относительно пола будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) υ = 1 м/с? Массой колес и трением пренебречь.

17. Снаряд, летевший со скоростью υ = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40 % от массы снаряда, полетел в противоположном направлении со скоростью u₁ = 150 м/с. Определить скорость u₂ большего осколка.

18. Из ружья массой m₁ = 5 кг вылетает пуля массой m₂ = 5 г со скоростью υ ₂ = 600 м/с. Найти скорость υ ₁ отдачи ружья.

19. На сколько переместится относительно берега лодка длиной
l = 3. 5 м и массой m₁ = 200 кг, если стоящий на корме человек массой m₂ = 80 кг переместится на нос лодки? Считать лодку расположенной перпендикулярно берегу.

20. Лодка длиной l = 3 м и массой m = 120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами m₁ = 60 кг и m₂ = 90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?

21. В деревянный шар массой m₁ = 8 кг, подвешенный на нити длиной l = 1. 8 м, попадает горизонтально летящая пуля массой m₂ = 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол α = 3⁰? Размером шара пренебречь. Удар пули считать прямым, центральным.

22. По небольшому куску мягкого железа, лежащему на наковальне массой m₁ = 300 кг, ударяет молот массой m₂ = 8 кг. Определить КПД η удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.

23. Шар массой m₁ = 3 кг движется со скоростью υ ₁ = 2 м/с и сталкивается с покоящимся шаром массой m₂ = 5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым и центральным.

24. Шар массой m₁ = 5 кг движется со скоростью υ ₁ = 1 м/с и сталкивается с покоящимся шаром массой m₂ = 2 кг. Определить скорости u₁ и u₂ шаров после удара. Удар считать абсолютно упругим, прямым и центральным.

25. Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью υ ₁ = 600 м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью υ ₂ = 580 м/с. С какой скоростью откатилось при этом орудие?

26. Из шахты глубиной h = 600 м поднимают клеть массой
m₁ = 3 т на канате, каждый метр которого имеет массу m = 1. 5 кг. Какая работа А совершается при поднятии клети на поверхность земли? Каков коэффициент полезного действия η подъемного устройства?

27. Пружина жесткостью k = 500 Н/м сжата силой F = 100 Н. Определить работу А внешней силы, дополнительно сжимающей пружину еще на Δ l = 2 см.

28. Из пружинного пистолета с жесткостью пружины
k = 150 Н/м был произведен выстрел пулей массой m = 8 г. Определить скорость υ пули при вылете ее из пистолета, если пружина сжата на Δ х = 4 см.

29. Налетев на пружинный буфер, вагон массой m = 16 т, двигавшийся со скоростью υ = 0. 6 м/с, остановился, сжав пружину на
Δ l = 8 см. Найти общую жесткость k пружин буфера.

30. Какая работа А должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой h = 40 м, наружным диаметром D = 3 м и внутренним диаметром d = 2 м? Плотность материала ρ принять равной 2. 8∙ 10³ кг/м³.

31. По касательной к шкиву маховика в виде диска диаметром
D = 75 см и массой m = 40 кг приложена сила F = 10 Н. Определить угловое ускорение ε и частоту вращения n маховика через время t = 10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь.

32. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3 с приобрел угловую скорость ω = 9 рад/с.

33. Нить с привязанными к ее концам грузами массами m₁ = 50 г и m₂ = 60 г перекинута через блок D = 4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение ε = 1. 5 рад/с². Трением и проскальзыванием нити по блоку пренебречь.

34. Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению φ = A∙ t + B∙ t³, где А = 2 рад/с,
В = 0. 2 рад/с³. Определить вращающий момент М, действующий на стержень через время t = 2 с после начала вращения, если момент инерции стержня J = 0. 048 кг∙ м².

35. Блок, имеющий форму диска массой m = 0. 4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами m₁ = 0. 3 кг и m₂ = 0. 7 кг. Определить силы натяжения нити Т₁ и Т₂ по обе стороны блока.

36. Сплошной цилиндр массой m = 0. 1 кг катится без скольжения с постоянной скоростью υ = 4 м/с. Определить кинетическую энергию Е цилиндра, время t до его остановки, если на него действует сила трения F =0. 1 Н.

37. Сплошной шар скатывается по наклонной плоскости, длина которой l = 1 м и угол наклона α = 30⁰. Определить скорость υ шара в конце наклонной плоскости. Трение шара о плоскость не учитывать.

38. Полый цилиндр массой m = 1 кг катится по горизонтальной поверхности со скоростью υ = 10 м/с. Определить силу F, которую необходимо приложить к цилиндру, чтобы остановить его на пути s = 2 м.

39. Маховик, имеющий форму диска массой m = 10 кг и радиусом
R = 0. 1 м, был раскручен до частоты ν = 120 мин^-1. Под действием силы трения диск остановился через t = 10 с. Найти момент сил трения М, считая его постоянным.

40. Обруч и диск скатываются с наклонной плоскости, составляющей угол α = 30⁰ с горизонтом. Чему равны их ускорения a в конце спуска? Силой трения пренебречь.

41. На скамье Жуковского сидит человек и держит на вытянутых руках гири массой m = 5 кг каждая. Расстояние от каждой гири до оси скамьи l₁ = 70 см. Скамья вращается с частотой n₁ = 1 c^-1. Как изменится частота вращения скамьи и какую работу А произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l₂ = 20 см? Момент инерции человека и скамьи вместе относительно оси I = 2. 5 кг∙ м².

42. На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью ω ₁ = 4 рад/с. С какой угловой скоростью ω ₂ будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи J = 5 кг∙ м². Длина стержня
l = 1. 8 м, масса m = 6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.

43. На скамье Жуковского сидит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью ω ₁ = 25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи Жуковского. С какой угловой скоростью ω ₂ будет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол α = 90⁰? Момент инерции человека и скамьи J равен 2. 5 кг∙ м², момент инерции колеса J₀ = 0. 5 кг∙ м².

44. Однородный стержень длиной l = 1. 0 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой m = 7 г, летящая перпендикулярно стержню и его оси. Определить массу М стержня, если в результате попадания пули он отклонится на угол α = 60⁰. Принять скорость пули υ = 360 м/с.

45. На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой n₁ = 8 мин^-1, стоит человек массой m₁ = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n₂ = 10 мин^-1. Определить массу m₂ платформы. Момент инерции человека рассчитывать как для материальной точки.

46. На краю неподвижной скамьи Жуковского диаметром D = 0. 8 м и массой m₁ = 6 кг стоит человек массой m₂ = 60 кг. С какой угловой скоростью ω начнет вращаться скамья, если человек поймает летящий на него мяч массой m = 0. 5 кг? Траектория мяча горизонтальна и проходит на расстоянии r = 0. 4 м от оси скамьи. Скорость мяча υ = 5 м/с.

47. Однородный стержень длиной l = 1. 0 м подвешен на горизонтальной оси, проходящей через верхний конец стержня. На какой угол α надо отклонить стержень, чтобы нижний конец стержня при прохождении положения равновесия имел скорость υ = 5 м/с?

48. Однородный стержень длиной l = 85 см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую скорость υ надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?

49. Карандаш длиной l = 15 см, поставленный вертикально, падает на стол. Какую угловую скорость ω и линейную скорость υ будут иметь в конце падения середина и верхний конец карандаша?

50. Диск, насаженный на вертикальную ось, вращается с постоянной угловой скоростью. Второй диск, одинаковый с первым, вначале находится в покое, а затем падает на первый диск и сцепляется с ним. Чему равно отношение кинетических энергий одного диска Е_к1 и получившейся комбинации из двух дисков Е_к2?

51. На стержне длиной l = 30 см укреплены два одинаковых грузика: один – в середине стержня, другой – на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т простых гармонических колебаний данного физического маятника. Массой стержня пренебречь.

52. Точка совершает простые гармонические колебания, уравнение которых x = A∙ sinω t, где А = 5 см, ω = 2 с^-1. В момент времени, когда точка обладала потенциальной энергией Е_п = 0. 1 мДж, на нее действовала возвращающая сила F = 5мН. Найти этот момент времени t.

53. Определить частоту ν простых гармонических колебаний диска радиусом R = 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.

54. Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.

55. Определить период Т колебаний математического маятника, если модуль максимального перемещения Δ r = 18 см и максимальная скорость υ _max = 16 см/с.

56. На гладком горизонтальном столе лежит шар массой
М = 200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью k = 500 Н/м. В шар попадает пуля массой m = 10 г, летящая со скоростью υ = 300 см/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду А и период Т колебаний шара.

57. Амплитуда гармонического колебания А = 5 см, период
Т = 4 с. Найти максимальную скорость υ _max колеблющейся точки и ее максимальное ускорение а_max.

58. Точка совершает гармонические колебания. Период колебаний Т = 2 с, амплитуда А = 50 мм, начальная фаза φ = 0. Найти скорость υ точки в момент времени, когда смещение точки от положения равновесия х = 25 мм.

59. Написать уравнение гармонического колебательного движения, если максимальное ускорение точки а_max = 49. 3 см/с², период колебаний Т = 2 с и смещение точки от положения равновесия в начальный момент времени х₀ = 25 мм.

60. К пружине подвешен груз. Максимальная кинетическая энергия груза Е_{к max} = 1 Дж. Амплитуда колебаний А = 5 см. Найти жесткость k пружины.

61. В баллоне емкостью V = 50 л находится сжатый водород при 27⁰С. После того как часть водорода выпустили, давление понизилось на p = 1∙ 10⁵ Па. Определить массу m выпущенного водорода. Процесс считать изотермическим.

62. В сосуде, имеющем форму шара, радиус которого r = 0. 1 м, находится m = 5. 6 г азота. До какой температуры можно нагреть сосуд, если его стенки выдерживают давление p = 5∙ 10⁵ Па?

63. При температуре T = 300 К и давлении p = 1. 2∙ 10⁵ Па плотность смеси водорода и азота ρ = 1 кг/м³. Определить молярную массу M смеси.

64. В баллоне емкостью V = 0. 8 м³ находится m₁ = 2 кг водорода и m₂ = 2. 9 кг азота. Определить давление p смеси, если температура окружающей среды 27⁰С.

65. До какой температуры можно нагреть запаянный сосуд, содержащий m = 36 г воды, чтобы он не разорвался, если известно, что стенки сосуда выдерживают p = 5∙ 10⁶ Па. Объем сосуда
V = 5 л.

66. При температуре 27⁰С и давлении p = 10⁶ Па плотность смеси кислорода и азота ρ = 12 г/дм³. Определить молярную массу M смеси.

67. В баллоне вместимостью V = 15 л находится аргон под давлением р₁ = 600 кПа и при температуре Т₁ = 300 К. Когда из баллона было взято некоторое количество газа, давление в баллоне понизилось до р₂ = 400 кПа, а температура установилась Т₂ = 260 К. Определить массу m аргона, взятого из баллона.

68. Два сосуда одинакового объема содержат кислород. В одном сосуде давление р₁ = 2 МПа и температура Т₁ = 800 К, в другом
р₂ = 2. 5 МПа, Т₂ = 200 К. Сосуды соединили трубкой и охладили находящийся в них кислород до температуры Т = 200 К. Определить установившееся в сосуде давление р.

69. Вычислить плотность ρ азота, находящегося в баллоне под давлением р = 2 МПа и имеющего температуру Т = 400 К.

70. Определить относительную молекулярную массу М_r газа, если при температуре Т = 154 К и давлении р = 2. 8 МПа он имеет плотность ρ = 6. 1 кг/м³.

71. Найти среднюю кинетическую энергию вращательного движения всех молекул, содержащихся в 0. 20 г водорода при температуре 27⁰С.

72. Давление идеального газа р = 10 мПа, концентрация молекул n = 2∙ 10¹² см^-3. Определить среднюю кинетическую энергию  поступательного движения одной молекулы и температуру Т газа.

73. Определить среднее значение полной кинетической энергии  одной молекулы аргона и водяного пара при температуре Т = 500 К.

74. Средняя кинетическая энергия поступательного движения молекул газа равна 15∙ 10^-21 Дж. Концентрация молекул n = 9∙ 10¹⁹ см^-3. Определить давление р газа.

75. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию молекулы этого газа при температуре Т = 300 К, если количество вещества ν этого газа равно
0. 5 моль.

76. Определить суммарную кинетическую энергию Е_к поступательного движения всех молекул газа, находящегося в сосуде вместимостью V = 3 л под давлением р = 540 кПа.

77. Количество вещества гелия ν = 1. 5 моль, температура Т = 120 К. Определить суммарную кинетическую энергию Е_к поступательного движения всех молекул этого газа.

78. Молярная внутренняя энергия U_m некоторого двухатомного газа равна 6. 02 кДж/моль. Определить среднюю кинетическую энергию 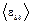вращательного движения одной молекулы этого газа. Газ считать идеальным.

79. Определить среднюю квадратичную скорость 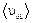молекул газа, заключенного в сосуд вместимостью V = 2 л под давлением р = 200 кПа. Масса газа m = 0. 3 г

80. В азоте взвешены мельчайшие пылинки, которые движутся так, как если бы они были очень крупными молекулами. Масса каждой пылинки равна 6∙ 10^-10 г. Газ находится при температуре Т = 400 К. Определить средние квадратичные скорости 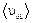, а также средние кинетические энергии 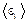поступательного движения молекул азота и пылинки.

81. Определить молярную массу М двухатомного газа и его удельные теплоемкости, если известно, что разность с_р – с_v удель-ных теплоемкостей этого газа равна 260 Дж/(кг∙ К).

82. Найти удельные с_р и с_v, а также молярные С_р и С_v теплоемкости углекислого газа.

83. Определить показатель адиабаты γ идеального газа, который при температуре Т = 350 К и давлении р = 0. 4 МПа занимает объем V = 300 л и имеет теплоемкость С_v = 857 Дж/К.

84. В сосуде вместимостью V = 6 л находится при нормальных условиях двухатомный газ. Определить теплоемкость С_v этого газа при постоянном объеме.

85. Определить молярные теплоемкости газа, если его удельные теплоемкости с_v = 10. 4 кДж/(кг∙ К) и с_р = 14. 6 кДж/(кг∙ К).

86. Вычислить удельные теплоемкости газа, зная, что его молярная масса М = 4∙ 10^-3 кг/моль и отношение теплоемкостей С_р/С_v = 1. 67.

87. Трехатомный газ под давлением р = 240 кПа и температуре 20⁰С занимает объем V =10 л. Определить теплоемкость С_р этого газа при постоянном давлении.

88. Одноатомный газ при нормальных условиях занимает объем V = 5 л. Вычислить теплоемкость С_v этого газа при постоянном объеме.

89. Найти удельную теплоемкость с_р газовой смеси, состоящей из количества ν ₁ = 3 кмоль аргона и количества ν ₂ = 2 кмоль азота.

90. Найти соотношение с_р/с_v для газовой смеси, состоящей из массы m₁ = 8 г гелия и массы m₂ = 16 г кислорода.

91. В сосуде емкостью V = 1 л содержится кислород массой m = 32 г. Определить среднее число соударений молекул в секунду 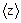при температуре Т = 100 К.

92. Определить среднюю длину 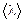 и среднюю продолжительность свободного пробега 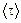молекул углекислого газа при температуре 400 К и давлении 1. 38 Па.

93. В сосуде емкостью V = 1 л находится m = 4. 4 г углекислого газа. Определить среднюю длину свободного пробега молекул .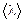

94. Определить коэффициент диффузии D гелия при давлении р = 1∙ 10⁶ Па и температуре 27⁰С.

95. Определить коэффициент внутреннего трения η кислорода при температуре Т = 400 К.

96. В сосуде емкостью V = 5 л содержится m = 40 г аргона. Определить среднее число соударений молекул в секунду 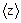 при температуре Т = 400 К.

97. Определить коэффициент внутреннего трения η воздуха при температуре Т = 100 К.

98. Определить коэффициент диффузии D азота при давлении р = 0. 5∙ 10⁵ Па и температуре 127⁰С.

99. Коэффициент внутреннего трения η кислорода при нормальных условиях 1. 9∙ 10^-4 кг/м∙ с. Определить коэффициент теплопроводности кислорода.

100. Коэффициент диффузии D водорода при нормальных условиях 9. 1∙ 10^-5 м²/с. Определить коэффициент теплопроводности æ водорода.

101. Какое количество теплоты Q нужно сообщить двум молям воздуха, чтобы он совершил работу в A = 1000 Дж: а) при изотермическом процессе; б) при изобарическом процессе.

102. Определить количество теплоты Q, которое надо сообщить кислороду объемом V = 50 л при его изохорном нагревании, чтобы давление газа повысилось на Δ р = 0. 5 МПа.

103. При изотермическом расширении азота при температуре Т = 280 К объем его увеличился в два раза. Определить: 1) совершенную при расширении газа работу А; 2) изменение Δ U внутренней энергии; 3) количество теплоты Q, полученное газом. Масса азота m = 0. 2 кг.

104. Объем водорода при изотермическом расширении при температуре Т = 300 К увеличился в n = 3 раза. Определить работу А, совершенную газом, и теплоту Q, полученную при этом. Масса водорода m = 200 г.

105. Идеальный газ совершает цикл Карно при температурах теплоприемника Т₂ = 290 К и теплоотдатчика Т₁ = 400 К. Во сколько раз увеличится коэффициент полезного действия η цикла, если температура теплоотдатчика возрастет до Т₁' = 600 К?

106. Идеальный газ совершает цикл Карно. Температура Т₁ теплоотдатчика в четыре раза (n = 4) больше температуры теплоприемника. Какую долю ω количества теплоты, полученную за один цикл от теплоотдатчика газ отдаст теплоприемнику?

107. Определить работу А₂ изотермического сжатия газа, совершающего цикл Карно, КПД которого η = 0. 4, если работа изотермического расширения равна А₁ = 8 Дж.

108. Совершая цикл Карно, газ отдал холодильнику 0. 65 теплоты, полученной от нагревателя. Определить температуру Т₂ холодильника, если температура нагревателя Т₁ = 400 К.

109. Найти изменение энтропии Δ S при нагревании m = 2 кг воды от 0 до 100⁰С и последующем превращении ее в пар при той же температуре.

110. Найти изменение энтропии Δ S при плавлении m = 2 кг свинца и дальнейшем его охлаждении от 327 до 0⁰С.

111. Найти массу m воды, вошедшей в стеклянную трубку с диаметром канала d₁ = 0. 8 мм, опущенную в воду на малую глубину. Считать смачивание полным.

112. Какую работу А надо совершить при выдувании мыльного пузыря, чтобы увеличить его объем от V₁ = 8 см³ до V₂ = 16см³? Считать процесс изотермическим.

113. Какая энергия Е выделится при слиянии двух капель ртути диаметром d₁ = 0. 8 мм и d₂ = 1. 2 мм в одну каплю.

114. Определить давление р внутри воздушного пузырька диаметром d = 4 мм, находящегося в воде у самой его поверхности.

115. Пространство между двумя стеклянными параллельными пластинками с площадью S = 100 см² каждая, расположенными на расстоянии l = 20 мкм друг от друга, заполнено водой. Определить силу F, прижимающую пластинки друг к другу. Считать мениск вогнутым с диаметром d, равным расстоянию между пластинками.

116. Глицерин поднялся в капиллярной трубке диаметром канала d = 1 мм на высоту h = 20 мм. Определить поверхностное натяжение α глицерина. Считать смачивание полным.

117. На сколько давление р воздуха внутри мыльного пузыря больше нормального атмосферного давления р₀, если диаметр пузыря d = 5 мм.

118. Воздушный пузырек диаметром d = 2. 2 мкм находится в воде у самой ее поверхности. Определить плотность ρ воздуха в пузырьке, если воздух над поверхностью воды находится при нормальных условиях.

119. Какую энергию надо затратить, чтобы выдуть мыльный пузырь диаметром d = 12 см? Каково будет добавочное давление внутри этого пузыря?

120. На нижнем конце трубки диаметром d = 0. 2 см повисла шарообразная капля воды. Найти диаметр этой капли.

121. Точечные зарядыQ₁ = 20 мкКл, Q₂ = -10 мкКл находятся на расстоянии d = 5 см друг от друга. Определить напряженность поля в точке, удаленной на r₁ = 3 см от первого и на r₂ = 4 см от второго заряда. Определить также силу 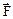, действующую в этой точке на точечный заряд Q = 1 мкКл.

122. Три одинаковых точечных заряда Q₁ = Q₂ = Q₃ = 2 нКл находятся в вершинах равностороннего треугольника со сторонами
а = 10 см. Определить модуль и направление силы 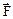, действующей на один из зарядов со стороны двух других.

123. Два положительных точечных заряда Q и 9Q закреплены на расстоянии d = 100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.

124. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол α. Шарики погружают в масло. Какова плотность ρ масла, если угол расхождения нитей при погружении в масло остается неизменным? Плотность материала шариков ρ ₀ = 1. 5∙ 10³ кг/м³, диэлектрическая проницаемость масла ε = 2. 2.

125. Четыре одинаковых заряда Q₁ = Q₂ = Q₃ = Q₄ = 40 нКл закреплены в вершинах квадрата со стороной а = 10 см. Найти силу 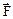, действующую на один из этих зарядов со стороны трех остальных.

126. В вершинах квадрата со стороной a = 0. 1 м расположены равные одноименные заряды Q. Потенциал создаваемого ими поля в центре квадрата φ = 500 В. Определить заряд Q.

127. В вершинах квадрата со стороной a = 0. 5 м расположены заряды одинаковой величины Q. В случае, когда два соседних заряда положительные, а два других – отрицательные, напряженность поля в центре квадрата Е = 144 В/м. Определить заряд Q.

128. Заряды по Q₁ = Q₂ = Q₃ = 1 нКл помещены в вершинах равностороннего треугольника со стороной a = 0. 2 м. Равнодействующая сил, действующая на четвертый заряд, помещенный на середине одной из сторон треугольника F = 0. 6 мкН. Определить этот заряд Q, напряженность Е и потенциал поля φ в точке его расположения.

129. Два шарика массой по m = 2 мг подвешены в общей точке на нитях длиной l = 0. 5 м. Шарикам сообщили заряд и нити разошлись на угол 90⁰. Определить напряженность E и потенциал поля φ в точке подвеса шарика.

130. Два одинаковых заряда находятся в воздухе на расстоянии
r₁ = 0. 1 м друг от друга. Напряженность поля в точке, удаленной на расстояние r₂ = 0. 06 м от одного и r₃ = 0. 08 м от другого заряда Е = 10 кВ/м. Определить потенциал поля φ в этой точке и значение зарядов Q.

131. Тонкий стержень длиной l = 20 см несет равномерно распределенный заряд τ = 0. 1 мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а = 20 см от его конца.

132. По тонкому полукольцу радиусом R = 10 см равномерно распределен заряд с линейной плотностью τ = 0. 1 мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

133. Тонкое кольцо несет распределенный заряд Q = 0. 2 мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, равноудаленной от всех точек кольца на расстояние r = 20 см. Радиус кольца R = 10 см.

134. Треть тонкого кольца радиусом R = 10 см несет распределенный заряд Q = 50 нКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

135. Бесконечный тонкий стержень, ограниченный с одной стороны, несет равномерно распределенный заряд с линейной плотностью τ = 0. 5 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а = 20 см от его начала.

136. По тонкому полукольцу равномерно распределен заряд Q = 20 мкКл с линейной плотностью τ = 0. 1 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

137. Четверть тонкого кольца радиусом R = 10 см несет равномерно распределенный заряд Q = 0. 05 мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

138. По тонкому кольцу равномерно распределен заряд Q =
10 нКл с линейной плотностью τ = 0. 01 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное радиусу кольца.

139. Две трети тонкого кольца радиусом R = 10 см несут равномерно распределенный с линейной плотностью τ = 0. 2 мкКл/м заряд. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

140. Пространство между двумя параллельными бесконечными плоскостями с поверхностной плотностью зарядов σ =
5∙ 10^-8 Кл/м² и σ = -9∙ 10^-8Кл/м² заполнено стеклом. Определить напряженность поля Е: а) между плоскостями; б) вне плоскостей.

141. Пылинка массой m = 200 мкг, несущая на себе заряд Q =
40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость υ = 10 м/с. Определить скорость υ ₀ пылинки до того как она влетела в поле.

142. Электрон, обладавший кинетической энергией Т = 10 эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов U = 8 В?

143. Найти отношение скоростей ионов Cu⁺⁺ и К⁺, прошедших одинаковую разность потенциалов.

144. Электрон с энергией Т = 400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 10 см. Определить минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее Q = -10 нКл.

145. Два точечных заряда Q₁ = 6 нКл и Q₂ = 3 нКл находятся на расстоянии d = 60 см друг от друга. Какую работу необходимо совершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?

146. Диполь с электрическим моментом р = 100 пКл∙ м свободно установился в однородном электрическом поле напряженностью Е = 200 кВ/м. Определить работу внешних сил, которую необходимо совершить для поворота диполя на угол α = 180⁰.

147. Четыре одинаковых капли ртути, заряженных до потенциала φ = 10 В, сливаются в одну. Каков потенциал φ ₁ образовавшейся капли?

148. Электрическое поле образовано бесконечно длинной заряженной нитью, линейная плотность заряда которой τ = 20 пКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r₁ = 8 см и r₂ = 12 см.

149. Со скоростью 2∙ 10⁷ м/с электрон влетает в пространство между обкладками плоского конденсатора в середине зазора в направлении, параллельном обкладкам. При какой минимальной разности потенциалов на обкладках электрон не вылетит из конденсатора, если длина конденсатора 10 см, а расстояние между его обкладками 1 см?

150. Заряд Q = 1 нКл притянулся к бесконечной плоскости, равномерно заряженной с поверхностной плотностью σ =
0. 2 мкКл/м². На каком расстоянии r от плоскости находился заряд, если работа сил поля по его перемещению равна А =
1 мкДж?

151. Конденсатор емкостью С₁ = 10 мкФ заряжен до напряжения U = 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный конденсатор емкостью С₂ = 20 мкФ.

152. Конденсаторы емкостями С₁ = 2 мкФ, С₂ = 5 мкФ и С₃ =
10 мкФ соединены последовательно и находятся под напряжением U = 850 В. Определить напряжение и заряд на каждом из конденсаторов.

153. Два одинаковых плоских воздушных конденсатора емкостью С₀ = 100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

154. Два металлических шарика радиусами

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: