 |
Внутренняя энергия идеального газа
|
|
|
|
Внутренняя энергия идеального газа
.
Скорости молекул:
а) средняя квадратичная
;
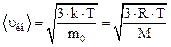б) средняя арифметическая
;
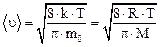в) наиболее вероятная
.
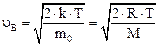Средняя длина свободного пробега молекулы
,
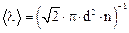где d – эффективный диаметр молекулы.
Среднее число столкновений молекулы в единицу времени
.
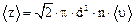Распределение молекул в потенциальном поле сил
,
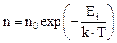где Еп – потенциальная энергия молекулы.
Барометрическая формула
.
Уравнение диффузии
,
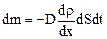где D – коэффициент диффузии; ρ – плотность; dS – элементарная площадка, перпендикулярная оси ОX.
Уравнение теплопроводности
dQ = -æ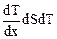 
,
где æ – теплопроводность.
Сила внутреннего трения
,
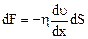где η – динамическая вязкость.
Коэффициент диффузии
.
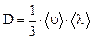Вязкость (динамическая)
.
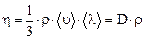Теплопроводность
æ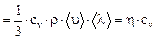 
,
где сυ – удельная изохорная теплоемкость.
Молярная теплоемкость идеального газа
а) изохорная
;
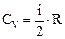б) изобарная
.
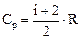Связь между удельной с и молярной С теплоемкостями
c = С/М.
Уравнение Майера
Ср – СV = R.
Первое начало термодинамики
dQ = dU + dA,
dU = ν ∙ Cv∙ dT,
dA = p∙ dV.
Работа расширения газа при процессе
а) изобарном
А = р∙ (V2 – V1) = ν ∙ R∙ (T2 – T1);
б) изотермическом
;
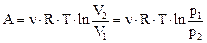в) адиабатном
А = ν ∙ Сv∙ (T1 – T2) =
,
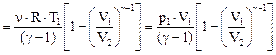где γ = Ср/Сv.
Работа расширения газа в общем случае
.
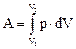Уравнения Пуассона
Термический КПД цикла
,
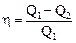где Q1 – теплота, полученная рабочим телом от теплоотдатчика; Q2 – теплота, переданная рабочим телом теплоприемнику.
Термический КПД цикла Карно
,
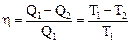где Т1 и Т2 – термодинамические температуры теплоотдатчика и теплоприемника.
|
|
|
Изменение энтропии при переходе из состояния 1 в состояние 2
.
Коэффициент поверхностного натяжения
α = F/l, или α = Δ E/Δ S,
где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости; Δ E – изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади Δ S поверхности этой пленки.
Формула Лапласа, выражающая давление р, создаваемое сферической поверхностью жидкости
р = 2∙ α /R,
где R – радиус сферической поверхности.
Высота подъема жидкости в капиллярной трубке
,
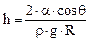где 
– краевой угол ( = 0 при полном смачивании стенок трубки жидкостью; = π при полном несмачивании); R – радиус канала трубки; ρ – плотность жидкости; g – ускорение свободного падения.
Высота подъема жидкости между двумя близкими и параллельными друг другу плоскостями
,
где d – расстояние между плоскостями.
Закон Кулона
,
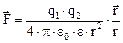где q1 и q2 – величины точечных зарядов; ε 0 – электрическая постоянная; ε – диэлектрическая проницаемость среды; r - расстояние между зарядами.
Напряженность электрического поля
.
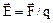Напряженность поля
а)точечного заряда
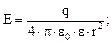
б) бесконечно длинной заряженной нити
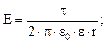
в) равномерно заряженной бесконечной плоскости
г) между двумя разноименно заряженными бесконечными плоскостями
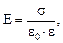
где τ = q/l – линейная плотность заряда; σ = q/S – поверхностная плотность заряда; r – расстояние до источника поля.
Электрическое смещение
Потенциал электрического поля
φ = П/q,
где П – потенциальная энергия точечного положительного заряда q, помещенного в данную точку поля.
Работа перемещения заряда в электростатическом поле
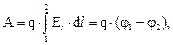
где φ 1 и φ 2 – потенциалы начальной и конечной точек.
Потенциал поля точечного заряда
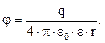
Связь потенциала с напряженностью:
|
|
|
а) в общем случае
;
б) в случае однородного поля
E = (φ 1 – φ 2)/d;
в) в случае поля, обладающего центральной или осевой симметрией
E = -dφ /dr.
Электрический момент диполя
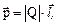
где Q – заряд;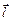 
– плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
|
|
|
